Translation and Commentary by Edward Rosen

THE JOHNS HOPKINS UNIVERSITY PRESS

Baltimore and London

Let no one untrained in geometry enter here.

NUREMBERG

JOHANNES PETREIUS

1543

XIX

FOREWORD BY ANDREAS OSIANDER

There have already been widespread reports about the novel hypotheses of this work, which declares that the earth moves whereas the sun is at rest in the center of the universeHence certain scholars, I have no doubt, are deeply offended and believe that the liberal arts, which were established long ago on a sound basis, should not be thrown into confusion. But if these men are willing to examine the matter closely, they will find that the author of this work has done nothing blameworthy. For it is the duty of an astronomer to compose the history of the celestial motions through careful and expert study. Then he must conceive and devise the causes of these motions or hypotheses about them. Since he cannot in any way attain to the true causes, he will adopt whatever suppositions enable the motions to be computed correctly from the principles of geometry for the future as well as for the past. The present author has performed both these duties excellently. For these hypotheses need not be true nor even probable. On the contrary, if they provide a calculus consistent with the observations, that alone is enough. Perhaps there is someone who is so ignorant of geometry and optics that he regards the epicyclc of Venus as probable, or thinks that it is the reason why Venus sometimes precedes and sometimes follows the sun by forty degrees and even more. Is there anyone who is not aware that from this assumption it necessarily follows that the diameter of the planet at perigee should appear more than four times, and the body of the planet more than sixteen times, as great as at apogee? Yet this variation is refuted by the experience of every age. In this science there are some other no less important absurdities, which need not be set forth at the moment. For this art, it is quite clear, is completely and absolutely ignorant of the causes of the apparent nonuniform motions. And if any causes are devised by the imagination, as indeed very many are, they are not put forward to convince anyone that are true, but merely to provide a reliable basis for computation. However, since different hypotheses are sometimes offered for one and the same motion (for example, eccentricity and an epicycle for the sun's motion), the astronomer will take as his first choice that hypothesis which is the easiest to grasp. The philosopher will perhaps rather seek the semblance of the truth. But neither of them will understand or state anything certain, unless it has been divinely revealed to him.

Therefore alongside the ancient hypotheses, which are no more probable, let us permit these new hypotheses also to become known, especially since they are admirable as well as simple and bring with them a huge treasure of very skillful observations. So far as hypotheses are concerned, let no one expect anything certain from astronomy, which cannot furnish it, lest he accept as the truth ideas conceived for another purpose, and depart from this study a greater fool than when he entered it. Farewell.

XX

LETTER OF NICHOLAS SCHÖNBERG

Some years ago word reached me concerning your proficiency, of which everybody constantly spoke. At that time I began to have a very high regard for you, and also to congratulate our contemporaries among whom you enjoyed such great prestige. For I had learned that you had not merely mastered the discoveries of the ancient astronomers uncommonly well but had also formulated a new cosmology. In it you maintain that the earth moves; that the sun occupies the lowest, and thus the central, place in the universe; that the eighth heaven remain perpetually motionless and fixed; and that, together with the elements included in its sphere, the moon, situated between the heavens of Mars and Venus, revolves around the sun in the period of a year. I have also learned that you have written an exposition of this whole system of astronomy, and have computed the planetary motions and set them down in tables, to the greatest admiration of all. Therefore with the utmost earnestness I entreat you, most learned sir, unless I inconvenience you, to communicate this discovery of yours to scholars, and at the earliest possible moment to send me your writings on the sphere of the universe together with the tables and whatever else you have that is relevant to this subject. Moreover, I have instructed Theodoric of Reden to have everything copied in your quarters at my expense and dispatched to me. If you gratify my desire in this matter, you will see that you are dealing with a man who is zealous for your reputation and eager to do justice to so fine a talent. Farewell.

XXI

TO HIS HOLINESS, POPE PAUL III,

NICHOLAS COPERNICUS' PREFACE

TO HIS BOOKS ON THE REVOLUTIONS

I can readily imagine, Holy Father, that as soon as some people hear that in this volume, which I have written about the revolutions of the spheres of the universe, I ascribe certain motions to the terrestrial globe, they will shout that I must be immediately repudiated together with this belief For I am not so enamored of my own opinions that I disregard what others may think of them. I am aware that a philosopher's ideas are not subject to the judgement of ordinary persons, because it is his endeavor to seek the truth in all things, to the extent permitted to human reason by God. Yet I hold that completely erroneous views should be shunned. Those who know that the consensus of many centuries has sanctioned the conception that the earth remains at rest in the middle of the heaven as its center would, I reflected, regard it as an insane pronouncement if I made the opposite assertion that the earth moves. Therefore I debated with myself for a long time whether to publish the volume which I wrote to prove the earth's motion or rather to follow the example of the Pythagoreans and certain others, who used to transmit philosophy's secrets only to kinsmen and friends, not in writing but by word of mouth, as is shown by Lysis' letter to Hipparchus. And they did so, it seems to me, not, as some suppose, because they were in some way jealous about their teachings, which would be spread around; on the contrary, they wanted the very beautiful thoughts attained by great men of deep devotion not to be ridiculed by those who are reluctant to exert themselves vigorously in any literary pursuit unless it is lucrative; or if they are stimulated to the nonacquisitive study of philosophy by the exhortation and example of others, yet because of their dullness of mind they play the same part among philosophers as drones among bees. When I weighed these considerations, the scorn which I had reason to fear on account of the novelty and unconventionality of my opinion almost induced me to abandon completely the work which I had undertaken.

But while I hesitated for a long time and even resisted, my friends drew me back. Foremost among them was the cardinal of Capua, Nicholas Schönberg, renowned in every field of learning. Next to him was a man who loves me dearly, Tiedemann Giese, bishop of Chelmno, a close student of sacred letters as well as of all good literature. For he repeatedly encouraged me and, sometimes adding reproaches, urgently requested me to publish this volume and finally permit it to appear after being buried among my papers and lying concealed not merely until the ninth year but by now the fourth period of nine years. The same conduct was recommended to me by not a few other very eminent scholars. They exhorted me no longer to refuse, on account of the fear which I felt, to make my work available for the general use of students of astronomy. Ile crazier my doctrine of the earth's motion now appeared to most people, the argument ran, so much the more admiration and thanks would it gain after they saw the publication of my writings dispel the fog of absurdity by most luminous proofs. Influenced therefore by these persuasive men and by this hope, in the end I allowed my friends to bring out an edition of the volume, as they had long besought me to do.

However, Your Holiness will perhaps not be greatly surprised that I have dared to publish my studies after devoting so much effort to working them out that I did not hesitate to put down my thoughts about the earth's motion in written fcrm too. But you are rather waiting to hear from me how it occurred to me to venture to conceive any motion of the earth, against the traditional opinion of astronomers and almost against common sense. I have accordingly no desire to from Your Holiness that I was impelled to consider a different system of deducing the motions of the universe's spheres for no other reason than the realization that astronomers do not agree among themselves in their investigations of this subject. For, in the first place, they are so uncertain about the motion of the sun and moon that they cannot establish and observe a constant length even for the tropical year. Secondly, in determining the motions not only of these bodies but also of the other five planets, they do not use the same principles, assumptions, and explanations of the apparent revolutions and motions. For while some employ only homocentrics, others utilize eccentrics and epicycles, and yet they do not quite reach their goal. For although those who put their faith in homocentrics showed that some nonuniform motions could be compounded in this way, nevertheless by this means they were unable to obtain any incontrovertible result in absolute agreement with the phenomena. On the other hand, those who devised the eccentrics seem thereby in large measure to have solved the problem of the apparent motions with appropriate calculations. But meanwhile they introduced a good many ideas which apparently contradict the first principles of uniform motion. Nor could they elicit or deduce from the eccentrics the principal consideration, that is, the structure of the universe and the true symmetry of its parts. On the contrary, their experience was just like some one taking from various places hands, feet, a head, and other pieces, very well depicted, it may be, but not for the representation of a single person; since these fragments would not belong to one another at all, a monster rather than a man would be put together from them. Hence in the process of demonstration or "method", as it is called, those who employed eccentrics are found either to have omitted something essential or to have admitted something extraneous and wholly irrelevant. This would not have happened to them, had they followed sound principles. For if the hypotheses assumed by them were not false, everything which follows from their hypotheses would be confirmed beyond any doubt. Even though what I am now saying may be obscure, it will nevertheless become clearer in the proper place.

For a long time, then, I reflected on this confusion in the astronomical traditions concerning the derivation of the motions of the universe's spheres. I began to be annoyed that the movements of the world machine, created for our sake by the best and most systematic Artisan of all, were not understood with greater certainty by the philosophers, who otherwise examined so precisely the most insignificant trifles of this world. For this reason I undertook the task of rereading the works of all the philosophers which I could obtain to learn whether anyone had ever proposed other motions of the universe's spheres than those expounded by the teachers of astronomy in the schools. And in fact first I found in Cicero that Hicetas supposed the earth to move. Later I also discovered in Plutarch that certain others were of this opinion. I have decided to set his words down here, so that they may be available to everybody:

Some think that the earth remains at rest. But Philolaus the Pythagorean believes that, like the sun and moon, it revolves around the fire in an oblique circle. Heraclides of Pontus, and Ecphantus the Pythagorean make the earth move, not in a progressive motion, but like a wheel in a rotation from west to east about its own center.

Therefore, having obtained the opportunity from these sources, I too began to consider the mobility of the earth. And even though the idea seemed absurd, nevertheless I knew that others before me had been granted the freedom to imagine any circles whatever for the purpose of explaining the heavenly phenomena. Hence I thought that I too would be readily permitted to ascertain whether explanations sounder than those of my predecessors could be found for the revolution of the celestial spheres on the assumption of some motion of the earth.

Having thus assumed the motions which I ascribe to the earth later on in the volume, by long and intense study I finally found that if the motions of the other planets are correlated with the orbiting of the earth, and are computed for the revolution of each planet, not only do their phenomena follow therefrom but also the order and size of all the planets and spheres, and heaven itself is so linked together that in no portion of it can anything be shifted without disrupting the remaining parts and the universe as a whole. Accordingly in the arrangement of the volume too I have adopted the following order. In the first book I set forth the entire distribution of the spheres together with the motions which I attribute to the earth, so that this book contains, as it were, the general structure of the universe. Then in the remaining books I correlate the motions of the other planets and of all the spheres with the movement of the earth so that I may thereby determine to what extent the motions and appearances of the other planets and spheres can be saved if they are correlated with the earth's motions. I have no doubt that acute and learned astronomers will agree with me if, as this discipline especially requires, they are willing to examine and consider, not superficially but thoroughly, what I adduce in this volume in proof of these matters. However, in order that the educated and uneducated alike may see that I do not run away from the judgement of anybody at all, I have preferred dedicating my studies to Your Holiness rather than to anyone else. For even in this very remote comer of the earth where I live you are considered the highest authority by virtue of the loftiness of your office and your love for all literature and astronomy too. Hence by your prestige and judgement you can easily suppress calumnious attacks although, as the proverb has it, there is no remedy for a backbite.

Perhaps there will be babblers who claim to be judges of astronomy although completely ignorant of the subject and, badly distorting some passage of Scripture to their purpose, will dare to find fault with my undertaking and censure it. I disregard them even to the extent of despising their criticism as unfounded. For it is not unknown that Lactantius, otherwise an illustrious writer but hardly an astronomer, speaks quite childishly about the earth's shape, when he mocks those who declared that the earth has the form of a globe. Hence scholars need not be surprised if any such persons will likewise ridicule me. Astronomy is written for astronomers. To them my work too will seem, unless I am mistaken, to make some contribution also to the Church, at the head of which Your Holiness now stands. For not so long ago under Leo X the Lateran Council considered the problem of reforming the ecclesiastical calendar. The issue remained undecided then only because the lengths of the year and month and the motions of the sun and moon were regarded as not yet adequately measured. From that time on, at the suggestion of that most distinguished man, Paul, bishop of Fossombrone, who was then in charge of this matter, I have directed my attention to a more precise study of these topics. But what I have accomplished in this regard, I leave to the judgement of Your Holiness in particular and of all other learned astronomers. And lest I appear to Your Holiness to promise more about the usefulness of this volume than I can fulfill, I now turn to the work itself.

NICHOLAS COPERNICUS'

REVOLUTIONS      Book One

INTRODUCTION

Among the many various literary and artistic pursuits which invigorate men's minds, the strongest affection and utmost zeal should, I think, promote the studies concerned with the most beautiful objects, most deserving to be known. This is the nature of the discipline which deals with the universe's divine revolutions, the asters' motions, sizes, distances, risings and settings, as well as the causes of the other phenomena in the sky, and which, in short, explains its whole appearance. What indeed is more beautiful than heaven, which of course contains all things of beauty? This is proclaimed by its very names [in Latin], caelum and mundus, the latter denoting purity and ornament, the former a carving. On account of heaven's transcendent perfection most philosophers have called it a visible god. If then the value of the arts is judged by the subject matter which they treat, that art will be by far the foremost which is labeled astronomy by some, astrology by others, but by many of the ancients, the consummation of mathematics. Unquestionably the summit of the liberal arts and most worthy of a free man, it is supported by almost all the branches of mathematics. Arithmetic, geometry, optics, surveying, mechanics and whatever others there are all contribute to it.

Although all the good arts serve to draw man's mind away from vices and lead it toward better things, this function can be more fully performed by this art, which also provides extraordinary intellectual pleasure. For when a man is occupied with things which he sees established in the finest order and directed by divine mana gement, will not the unremitting contemplation of them and a certain familiarity with them stimulate him to the best and to admiration for the Maker of everything, in whom are all happiness and every good? For would not the godly Psalmist [92:4] in vain declare that he was made glad through the work of the Lord and rejoiced in the works of His hand s, were we not drawn to the contemplation of the highest good by this means, as though by a chariot?

The great benefit and adornment which this art confers on the commonwealth (not to mention the countless advantages to individuals) are most excellently observed by Plato. In the Laws, Book VII, he thinks that it should be cultivated chiefly because by dividing time into groups of days as months and years, it would keep the state alert and attentive to the festivals and sacrifices. Whoever denies its necessity for the teacher of any branch of higher learning is thinking foolishly, according to Plato. In his opinion it is highly unlikely that anyone lacking the requisite knowledge of the sun, moon, and other heavenly bodies can become and be called godlike.

However, this divine rather than human science, which investigates the loftiest subjects, is not free from perplexities. The main reason is that its principles and assumptions, called "hypotheses" by the Greeks, have been a source of disagreement, as we see, among most of those who undertook to deal with this subject, and so they did not rely on the same ideas. An additional reason is that the motion of the planets and the revolution of the stars could not be measured with numerical precision and completely understood except with the passage of time and the aid of many earlier observations, through which this knowledge was transmitted to posterity from hand to hand, so to say. To be sure, Claudius Ptolemy of Alexandria, who far excels the rest by his wonderful skill and industry, brought this entire art almost to perfection with the help of observations extending over a period of more than four hundred years, so that there no longer seemed to be any gap which he had not closed. Nevertheless very many things, as we perceive, do not agree with the conclusions which ought to follow from his system, and besides certain other motions have been discovered which were not yet 2 known to him. Hence Plutarch too, in discussing the sun's tropical year, says that so far the motion of the heavenly bodies has eluded the skill of the astronomers. For, to use the year itself as an example, it is well known, I think, how different the opinions concerning it have always been, so that many have abandoned all hope that an exact determination of it could be found. The situation is the 1 same with regard to other heavenly bodies.

Nevertheless, to avoid giving the impression that this difficulty is an excuse for indolence, by the grace of God, without whom we can accomplish nothing, I shall attempt a broader inquiry into these matters. For, the number of aids we have to assist our enterprise grows with the interval of time extending from 2 the originators of this art to us. Their discoveries may be compared with what I have newly found. I acknowledge, moreover, that I shall treat many topics differently from my predecessors, and yet I shall do so thanks to them, for it was they who first opened the road to the investigation of these very questions.

THE UNIVERSE IS SPHERICAL    Chapter 1

First of all, we must note that the universe is spherical. The reason is either that, of all forms, the sphere is the most perfect, needing no joint and being a complete whole, which can be neither increased nor diminished; or that it is the most capacious of figures, best suited to enclose and retain all things; or even that all the separate parts of the universe, I mean the sun, moon, planets and stars, are seen to be of this shape; or that wholes strive to be circumscribed by this boundary, as is apparent in drops of water and other fluid bodies when they seek to be self-contained. Hence no one will question the attribution of this form to the divine bodies.

THE EARTH TOO IS SPHERICAL    Chapter 2

The earth also is spherical, since it presses upon its center from every direction. Yet it is not immediately recognized as a perfect sphere on account of the great height of the mountains and depth of the valleys. They scarcely alter the general sphericity of the earth, however, as is clear from the following considerations. For a traveler going from any place toward the north, that pole of the daily rotation gradually climbs higher, while the opposite pole drops down an equal amount. More stars in the north are seen not to set, while in the south certain stars are no longer seen to rise. Thus Italy does not see Canopus, which is visible in Egypt; and Italy does see the River's last star, which is unfamiliar to our area in the colder region. Such stars, conversely, move higher in the heavens for a traveller heading southward, while those which are high in our sky sink down. Meanwhile, moreover, the elevations of the poles have the same ratio everywhere to the portions of the earth that have been traversed. This happens on no other figure than the sphere. Hence the earth too is evidently enclosed between poles and is therefore spherical. Furthermore, evening eclipses of the sun and moon are not seen by easterners, nor morning eclipses by westerners, while those occurring in between are seen later by easterners but earlier by westerners.

The waters press down into the same figure also, as sailors are aware, since land which is not seen from a ship is visible from the top of its mast. On the other hand, if a light is attached to the top of the mast, as the ship draws away from land, those who remain ashore see the light drop down gradually until it finally disappears, as though setting. Water, furthermore, being fluid by nature, manifestly always seeks the same lower levels as earth and pusehs up from the shore no higher than its rise permits. Hence whatever land emerges out of the ocean is admittedly that much higher.

HOW EARTH FORMS A SINGLE SPHERE    Chapter 3
WITH WATER

Pouring forth its seas everywhere, then, the ocean envelops the earth and fills its deeper chasms. Both tend toward the same center because of their heaviness. Accordingly there had to be less water than land, to avoid having the water engulf the entire earth and to have the water recede from some portions of the land and from the many islands lying here and there, for the preservation of living creatures For what are the inhabited countries and the mainland itself but an island larger than, the others?

We should not heed certain peripatetics who declared that the entire body of water is ten times greater than all the land. For, according to the conjecture which they accepted, in the transmutation of the elements as one unit of earth dissolves, it becomes ten units of water. They also assert that the earth bulges out to some extent as it does because it is not of equal weight everywhere on account of its cavities, its center of gravity being different from its center of magnitude. But they err through ignorance of the art of geometry. For they do not realize that the water cannot be even seven times greater and still leave any part of the land dry, unless earth as a whole vacated the center of gravity and yielded that position to water, as if the latter were heavier than itself For, spheres are to each other as the cubes of their diameters. Therefore, if earth were the eighth part to seven parts of water, earth's diameter could not be greater than the distance from [their joint] center to the circumference of the waters. So far are they from being as much as ten times greater [than the land].

Moreover, there is no difference between the earth's centers of gravity and magnitude. This can be established by the fact that from the ocean inward the curvature of the land does not mount steadily in a continuous rise. If it did, it would keep the sea water out completely and in no way permit the inland seas and such vast gulfs to intrude. Furthermore, the depth of the abyss would never stop increasing from the shore of the ocean outward, so that no island or reef or any form of land would be encountered by sailors on the longer voyages. But it is well known that almost in the middle of the inhabited lands barely fifteen furlongs remain between the eastern Mediterranean and the Red Sea. On the other hand, in his Geography Ptolemy extended the habitable area halfway around the world. Beyond that meridian, where he left unknown land, the modem have added Cathay and territory as vast as sixty degrees of longitude, so that now the earth is inhabited over a greater stretch of longitude than is left for the ocean. To these regions, moreover, should be added the islands discovered in our time under the rulers of Spain and Portugal, and especially America, named after the ship's captain who found it. On account of its still undisclosed size it is thought to be a second group of inhabited countries. There are also many other islands, heretofore unknown. So little reason have we to marvel at the existence of antipodes or antichthones. Indeed, geometrical reasoning about the location of America compels us to believe that it is diametrically opposite the Ganges district of India.

From all these facts, finally, I think it is clear that land and water together press upon a single center of gravity; that the earth has no other center of magnitude; i that, since earth is heavier, its gaps are filled with water; and that consequently there is little water in comparison with land, even though more water perhaps appears on the surface.

The earth together with its surrounding waters must in fact have such a shape as its shadow reveals, for it eclipses the moon with the arc of a perfect circle. Therefore the earth is not flat, as Empedocles and Anaximenes thought; nor drum-shaped, as Leucippus; nor bowl-shaped, as Heraclitus; nor hollow in another way, as Democritus; nor again cylindrical, as Ansaximander; nor does its lower side extend infinitely downward, the thickness diminishing toward the bottom, as Xenophanes taught; but it is perfectly round, as the philosophers hold.

THE MOTION OF THE BEAVENLY BODIES    Chapter 4
IS UNIFORM, ETERNAL, AND CIRCULAR OR
COMPOUNDED OF CIRCULAR MOTIONS

I shall now recall to mind that the motion of the heavenly bodies is circular, since the motion appropriate to a sphere is rotation in a circle. By this very act the sphere expresses its form as the simplest body, wherein neither beginning nor end can be found, nor can the one be distinguished from the other, while the sphere itself traverses the same points to return upon itself.

In connection with the numerous [celestial] spheres, however, there are many Motions. The most conspicuous of all is the daily rotation, which the Greeks call nuchthemeron, that is, the hiterval of a day and a night. The entire universe, with the exception of the earth, is conceived as whirling from cast to west in this rotation. It is recognized as the common measure of all motions, since we even compute time itself chiefly by the number of days.

Secondly, we see other revolutions as advancing in the opposite direction, that is, from west to east; I refer to those of the sun, moon, and five planets. The sun thus regulates the year for us, and the moon the month, which are also very familiar Periods of time. In like manner each of the other five planets completes its own orbit.

Yet [these motions] differ in many ways [from the daily rotation or first motion]. In the first place, they do not swing around the same poles as the first motion, but run obliquely through the zodiac. Secondly, these bodies are not seen moving uniformly in their orbits, since the sun and moon are observed to be sometimes slow, at other times faster in their course. Moreover, we see the other five planets also retrograde at times, and stationary at either end [of the regression]. And whereas the sun always advances along its own direct path, they wander in various ways, straying sometimes to the south and sometimes to the north; that is why they are called "planets" [wanderers]. Furthermore, they are at times nearer to the earth, when they are said to be in perigee; at other times they are farther away, when they are said to be in apogee.

We must acknowledge, nevertheless, that their motions are circular or compounded of several circles, because these nonuniformities recur regularly according to a constant law. This could not happen unless the motions were circular, since only the circle can bring back the past. Thus, for example, by a composite motion of circles the sun restores to us the inequality of days and nights as well as the is four seasons of the year. Several motions are discerned herein, because a simple heavenly body cannot be moved by a single sphere nonuniformly. For this nonuniformity would have to be caused either by an inconstancy, whether imposed from without or generated from within, in the moving force or by an alteration in the revolving body. From either alternative, however, the intellect shrinks. It is improper to conceive any such defect in objects constituted in the best order.

It stands to reason, therefore, that their uniform motions appear nonuniform to us. The cause may be either that their circles have poles different [from the earth's] or that the earth is not at the center of the circles on which they revolve. To us who watch the course of these planets from the earth, it happens that our eye does not keep the same distance from every part of their orbits, but on account of their varying distances these bodies seem larger when nearer than when farther away (as has been proved in optics). Likewise, in equal arcs of their orbits their motions will appear unequal in equal times on account of the observer's varying distance. Hence I deem it above all necessary that we should carefully scrutinize the relation of the earth to the heavens lest, in our desire to examine the loftiest objects, we remain ignorant of things nearest to us, and by the same error attribute to the celestial bodies what belongs to the earth.

DOES CIRCULAR MOTION SUIT THE EARTH?    Chapter 5
WHAT IS ITS POSITION?

Now that the earth too has been shown to have the form of a sphere, we must in my opinion see whether also in this case the form entails the motion, and what place in the universe is occupied by the earth. Without the answers to these questions it is impossible to find the correct explanation of what is seen in the heavens. To be sure, there is general agreement among the authorities that the earth is at rest in the middle of the universe. They hold the contrary view to be inconceivable or downright silly. Nevertheless, if we examine the matter more carefully, we shall see that this problem has not yet been solved, and is therefore by no means to be disregarded.

Every observed change of place is caused by a motion of either the observed object or the observer or, of course, by an unequal displacement of each. For when things move with equal speed in the same direction, the motion is not perceived, as between the observed object and the observer, I mean It is the earth, however, from which the celestial ballet is beheld in its repeated performances before our eyes. Therefore, if any motion is ascribed to the earth, in all things outside it the same motion will appear, but in the opposite direction, as though they were moving past it. Such in particular is the daily rotation, since it seems to involve the entire universe except the earth and what is around it. However, if you grant that the heavens have no part in this motion but that the earth rotates from west to east, upon earnest consideration you will find that this is the actual situation concerning the apparent rising and setting of the sun, moon, stars and planets. Moreover since the heavens, which enclose and provide the setting for everything, constitute the space common to all things, it is not at first blush clear why motion should not be attributed rather to the enclosed than to the enclosing, to the thing located in space rather than to the framework of space. This opinion was indeed maintained by Heraclides and Ecphantus, the Pythagoreans, and by Eficetas of Syracuse, according to Cicero. They rotated the earth in the middle of the universe, for they ascribed the setting of the stars to the earth's interposition, and their rising to its withdrawal.

If we assume its daily rotation, another and no less important question follows concerning the earth's position. To be sure, heretofore there has been virtually unanimous acceptance of the belief that the middle of the universe is the earth. Anyone who denies that the earth occupies the middle or center of the universe may nevertheless assert that its distance (therefrom] is insignificant in comparison with [the distance of] the sphere of the fixed stars, but perceptible and noteworthy in relation to the spheres of the sun and the other planets. He may deem this to be the reason why their motions appear nonuniform, as conforming to a center other than the center of the earth. Perhaps he can [thereby] produce a not inept explanation of the apparent nonuniform motion. For the fact that the same planets are observed nearer to the earth and farther away necessarily proves that the center of the earth is not the center of their circles. It is less clear whether the approach and withdrawal are executed by the earth or the planets.

It Will occasion no surprise if, in addition to the daily rotation, some other motion is assigned to the earth. That the earth rotates, that it also travels with several motions, and that it is one of the heavenly bodies are said to have been the opnions of Philolaus the Pythagorean. He was no ordinary astronomer, inasmuch as Plato did not delay going to Italy for the sake of visiting him, as Plato's biographers report.

But many have thought it possible to prove by geometrical reasoning that the earth is in. the middle of the universe; that being like a point in relation to the immense heavens, it serves as their center; and that it is motionless because, when the universe moves, the center remains unmoved, and the things newest to the center are carried most slowly.

THE IMMENSITY OF THE HEAVENS        Chapter 6
COMPARED TO THE SIZE OF THE EARTH

The massive bulk of the earth does indeed shrink to insignificance in comparison with the size of the heavens. This can be ascertained from the fact that the boundary circles (for that is the translation of the Greek term horizons) bisect the entire sphere of the heavens. This could not happen if the earth's size or distance from the universe's center were noteworthy in comparison with the heavens. For, a circle that bisects a sphere passes through its center, and is the greatest circle that can be described on it.

Thus, let circle ABCD be a horizon, and let the earth, from which we do our observing, be E, the center of the horizon, which separates what is seen from what is not seen. Now, through a dioptra or horoscopic instrument or water level placed at E, let the first point of the Crab be sighted rising at point C, and at that instant the first point of the Goat is perceived to be setting at A. Then A, E, and C are on a straight line through the dioptra. This line is evidently a diameter of the ecliptic, since six visible signs form a semicircle, and E, the [line's] center, is identical with the horizon's center. Again, let the signs shift their position until the first point of the Goat rises at B. At that time the Crab win also be observed setting at D. BED will be a straight line and a diameter of the ecliptic. But, as we have already seen, ABC also is a diameter of the same circle. Its center, obviously, is the intersection [of the diameters]. A horizon, then, in this way always bisects the ecliptic, which is a great circle of the sphere. But on a sphere, if a circle bisects any great circle, the bisecting circle is itself a great circle. Consequently a horizon is one of the great circles, and its center is clearly identical with the center of the ecliptic.

Yet a line drawn from the earth's surface [to a point in the firmament] must be distinct from the line drawn from the earth's center [to the same point]. Nevertheless, because these lines are immense in relation to the earth, they become like parallel lines [III, 15]. Because their terminus is enormously remote they appear to be a single line. For in comparison with their length the space enclosed by them becomes imperceptible, as is demonstrated in optics. This reasoning certainly makes it quite clear that the heavens are immense by comparison with the earth and present the aspect of an infinite magnitude, while on the testimony of the senses the earth is related to the heavens as a point to a body, and a finite to an infinite magnitude.

But no other conclusion seems to have been established. For it does not follow that the earth must be at rest in the middle of the universe. Indeed, a rotation in twenty-four hours of the enormously vast universe should astonish us even more than a rotation of its least part, which is the earth. For, the argument a that the center is motionless, and what is nearest the center moves the least, does not prove that the earth is at rest in the middle of the universe.

To take a similar case, suppose you say that the heavens rotate but the poles are stationary, and what is closest to the poles-moves the least. The Little Bear, for example, being very close to the pole, is observed to move much more slowly than the Eagle or the Little Dog because it describes a smaller circle. Yet all these constellations belong to a single sphere. A sphere's movement, vanishing at its axis, does not permit an equal motion of all its parts. Nevertheless these are brought

But things separated by the diversity of their situations are subject to a very different relation: those enclosed in a smaller orbit revolve faster than those traversing a bigger circle. Thus Saturn, the highest of the planets, revolves in thirty years; the moon, undoubtedly the nearest to the earth, completes its course in a month; and to close the series, it will be thought, the earth rotates in the period of a day and a night. Accordingly the same question about the daily rotation emerges again. On the other hand, likewise still undetermined is the earth's position, which has been made even less certain by what was said above. For that proof establishes no conclusion other than the heavens' unlimited size in relation to the earth. Yet how far this immensity extends is not at all clear. At the opposite extreme are the very tiny indivisible bodies called "atoms". Being imperceptible, they do not immediately constitute a visible body when they are taken two or a few at a time. But they can be multiplied to such an extent that in the end there are enough of them to combine in a perceptible magnitude. The same may be said also about the position of the earth. Although it is not in the center of the universe, nevertheless its distance therefrom is still insignificant, especially in relation to the sphere of the fixed stars.

WHY THE ANCIENTS THOUGHT THAT        Chapter 7
THE EARTH REMAINED AT REST IN
THE MIDDLE OF THE UNIVERSE AS ITS CENTER

Accordingly, the ancient philosophers sought to establish that the earth remains at rest in the middle of the universe by certain other arguments. As their main reason, however, they adduce heaviness and lightness. Earth is in fact the heaviest element, and everything that has weight is borne toward it in an effort to reach its inmost center. The earth being spherical, by their own nature heavy objects are carried to it from all directions at right angles to its surface. Hence, if they were not checked at its surface, they would collide at its center, since a straight line perpendicular to a horizontal plane at its point of tangency with a sphere leads to the [sphere's] center. But things brought to the middle, it seem to follow, come to rest at the middle. All the more, then, will the entire earth be at rest in the middle, and as the recipient of every falling body it will remain motionless thanks to its weight.

In like manner, the ancient philosophers analyze motion and its nature in a further attempt to confirm their conclusion. Thus, according to Aristotle, the motion of a single simple body is simple; of the simple motions, one is straight and the other is circular; of the straight motions, one is upward and the other is downward. Hence every simple motion is either toward the middle, that is, downward; or away from the middle, that is, upward; or around the middle, that is, circular. To be carried downward, that is, to seek the middle, is a property only of earth and water, which are considered heavy; on the other hand, air and fire, which are endowed with lightness, move upward and away from the middle. To these four elements it seems reasonable to assign rectilinear motion, but to the heavenly bodies, circular motion around the middle. This is what Aristotle says [Heavens, I, 2; II, 14].

Therefore, remarks Ptolemy of Alexandria [Syntaxis, 1, 7], if the earth were to move, merely in a daily rotation, the opposite of what was said above would have to occur, since a motion would have to be exceedingly violent and its speed unsurpassablc to carry the entire circumference of the earth around in twenty-four hours. But things which undergo an abrupt rotation seem utterly unsuited to gather [bodies to themselves], and seem more likely, if they have been produced by combination, to fly apart unless they are held together by some bond. The earth would long ago have burst asunder, he says, and dropped out of the skies (a quite preposterous notion); and, what is more, living creatures and any other loose weights would by no means remain unshaken. Nor would objects falling in a straight line descend perpendicularly to their appointed place, which would meantime have been withdrawn by so rapid a movement. Moreover, clouds and anything else floating in the air would be seen drifting always westward.

THE INADEQUACY OF THE PREVIOUS    Chapter 8
ARGUMENTS AND A REFUTATION OF TIMM

For these and similar reasons forsooth the ancients insist that the earth remains at rest in the middle of the universe, and that this is its status beyond any doubt. Yet if anyone believes that the earth rotates, surely he will hold that its motion is natural, not violent. But what is in accordance with nature produces effects contrary to those resulting from violence, since things to which force or violence is applied must disintegrate and cannot long endure. On the other hand, that which is brought into existence by nature is well-ordered and preserved in its best state. Ptolemy has no cause, then, to fear that the earth and everything earthly will be disrupted by a rotation created through natures handiwork, which is quite different from what art or human intelligence can accomplish.

But why does he not feel this apprehension even more for the universe, whose motion must be the swifter, the bigger the heavens are than the earth? Or have the heavens become immense because the indescribable violence of their motion drives them away from the center? Would they also fall apart if they came to a halt? Were this reasoning sound, surely the size of the heavens would likewise grow to infinity. For the higher they are driven by the power of their motion, the faster that motion will be, since the circumference of which it must make the circuit in the period of twenty-four hours is constantly expanding; and, in turn, as the velocity of the motion mounts, the vastness of the heavens is enlarged. In this way the speed will increase the size, and the size the speed, to infinity. Yet according to the fimiliar ear axiom of physics that the infinite cannot be traversed 5 or moved in any way, the heavens will therefore necessarily remain stationary.

But beyond the heavens there is said to be no body, no space, no void, abso- lutely nothing, so that there is nowhere the heavens can go. In that case it is really astonishing if something can be held in check by nothing. If the heavens are infinite, however, and finite at their inner concavity only, there will perhaps be more reason to believe that beyond the heavens there is nothing. For, every single thing, no matter what size it attains, will be inside them, but the heavens will abide motionless. For, the chief contention by which it is sought to prove that the universe is finite is its motion. Let us therefore leave the question whether the universe is finite or infinite to be discussed by the natural philosophers.

We regard it as a certainty that the earth, enclosed between poles, is bounded by a spherical surface. Why then do we still hesitate to grant it the motion appropriate by nature to its form rather than attribute a movement to the entire universe, whose limit is unknown and unknowable? Why should we not admit, with regard to the daily rotation, that the appearance is in the heavens and the reality in the earth? This situation closely resembles what Vergil's Aeneas says:

Forth from the harbor we sail, and the land and the cities slip backward [Aeneid, III, 72].

For when a ship is floating calmly along, the sailors see its motion mirrored in everything outside, while on the other hand they suppose that they are stationary, together with everything on board. In the same way, the motion of the earth can unquestionably produce the impression that The entire universe is rotating.

Then what about the clouds and the other things that hang in the air in any manner whatsoever, or the bodies that fall down, and conversely those that rise aloft? We would only say that not merely the earth and the watery element joined with it have this motion, but also no small part of the air and whatever is Raked in the same way to the earth. Ile reason may be either that the nearby air, mingling with earthy or watery matter, conforms to the same nature as the earth, or that the air's motion, acquired from the earth by proximity, shares without resistance in its unceasing rotation. No less astonishingly, on the other hand, is the celestial movement declared to be accompanied by the uppermost belt of air. This is indicated by those bodies that appear suddenly, I mean, those that the Greeks called "comets" and "bearded stars". Like the other heavenly bodies, they rise and set. They are thought to be generated in that region. That part of the air, we can maintain, is unaffected by the earth's motion on account of its great distance from the earth. The air closest to the earth will accordingly seem to be still. And so will the things suspended in it, unless they are tossed to and fro, as indeed they are, by the wind or some other disturbance. For what else is the wind in the air but the wave in the sea?

We must in fact avow that the motion of falling and rising bodies in the framework of the universe is twofold, being in every case a compound of straight and circular. For, things that sink of their own weight, being predominantly earthy, undoubtedly retain the same nature as the whole of which they are parts. Nor is the explanation different in the case of those things, which, being fiery, are driven forcibly upward. For also fire here on the earth feeds mainly on earthy matter, and flame is defined as nothing but blazing smoke. Now it is a property of fire to expand what it enters. It does this with such great force that it cannot be prevented in any way by any device from bursting through restraints and completing its work. But the motion of expansion is directed from the center to the circumference. Therefore, if any part of the earth is set afire, it is carried from the middle upwards. Hence the statement that the motion of a simple body is simple holds true in particular for circular motion, as long as the simple body abides in its natural place and with its whole. For when it is in place, it has none but circular motion, which remains wholly within itself like a body at rest. Rectilinear motion, however, affects things which leave their natural place or arc thrust out of it or quit it in any manner whatsoever. Yet nothing is so incompatible with the orderly arrangement of the universe and the design of the totality as something out of place. Therefore rectilinear motion occurs only to things that are not in proper condition and are not in complete accord with their nature, when they are separated from their whole and forsake its unity.

Furthermore, bodies that are carried upward and downward, even when deprived of circular motion, do not execute a simple, constant, and uniform motion. For they cannot be governed by their lightness or by the impetus of their weight. Whatever falls moves slowly at first but increases its speed as it drops. On the other hand, we see this earthly fire (for we behold no other), after it has been lifted up high, slacken all at once, thereby revealing the reason to be the violence applied to the earthy matter. Circular motion, however, always rolls along uniformly, since it has an unfailing cause. But rectilinear motion has a cause that quickly stops functioning. For when rectilinear motion brings bodies to their own place, they cease to be heavy or light, and their motion ends. Hence, since circular motion belongs to wholes, but parts have rectilinear motion in addition, we can say that "circular" subsists with "rectilinear" as "being alive" with "being sick". Surely Aristotle's division of simple motion into three types, away from the middle, toward the middle, and around the middle, will be construed merely as a logical exercise. In like manner we distinguish line, point, and surface, even though one cannot exist without another, and none of them without body.

As a quality, moreover, immobility is deemed nobler and more divine than change and instability, which are therefore better suited to the earth than to the universe. Besides, it would seem quite absurd to attribute motion to the framework of space or that which encloses the whole of space, and not, more appropriately, to that which is enclosed and occupies some space, namely, the earth. Last of all, the planets obviously approach closer to the earth and recede farther from it. Then the motion of a single body around the middle, which is thought to be the center of the earth, will be both away from the middle and also toward it. Motion around the middle, consequently, must be interpreted in a more general way, the sufficient condition being that each such motion encircle its own center. You see, then, that all these arguments make it more likely that the earth moves than that it is at rest. This is especially true of the daily rotation, as particularly appropriate to the earth. This is enough, in my opinion, about the first part of the question.

CAN SEVERAL MOTIONS BE ATTRIBUTED       Chapter 9
TO THE EARTH? THE CENTER OF THE UNIVERSE

Accordingly, since nothing prevents the earth from moving, I suggest that we should now consider also whether several motions suit it, so that it can be regarded as one of the planets. For, it is not the center of all the revolutions. This is indicated by the planets, apparent nonuniform motion and their varying distances from the earth. These phenomena cannot be explained by circles concentric with the earth. Therefore, since there are many centers, it will not be by accident that the further question arises whether the center of the universe is identical with the center of terrestrial gravity or with some other point. For my part I believe that gravity is nothing but a certain natural desire, which the divine providence of the Creator of all things has implanted in parts, to gather as a unity and a whole by combining in the form of a globe. This impulse is present, we may suppose, also in the sun, the moon, and the other brilliant planets, so that through its operation they remain in that spherical shape which they display. Nevertheless, they swing round their circuits in divers ways. If, then, the earth too moves in other ways, for example, about a center, its additional motions must likewise be reflected in many bodies outside it. Among these motions we find the yearly revolution. For if this is transformed from a solar to a terrestrial movement, with the sun acknowledged to be at rest, the risings and settings which bring the zodiacal signs and fixed stars into view morning and evening will appear in the same way. The stations of the planets, moreover, as well as their retrogradations and [resumptions of] forward motion will be recognized as being, not movements of the planets, but a motion of the earth, which the planets borrow for their own appearances. Lastly, it will be realized that the sun occupies the middle of the universe. All these facts are disclosed to us by the principle governing the order in which the planets follow one another, and by the harmony of the entire universe, if only we look at the matter, as the saying goes, with both eyes.

THE ORDER OF THE HEAVENLY SPHERES    Chapter 10

Of all things visible, the highest is the heaven of the fixed stars. This, I see, is doubted by nobody. But the ancient philosophers wanted to arrange the planets in accordance with the duration of the revolutions. Their principle assumes that of objects moving equally fast, those farther away seem to travel more slowly, as is proved in Euclid's Optics. The moon revolves in the shortest period of time because, in their opinion, it runs on the smallest circle as the nearest to the earth. The highest planet, on the other hand, is Saturn, which completes the biggest circuit in the longest time. Below it is Jupiter, followed by Mars.

With regard to Venus and Mercury, however, differences of opinion are found. For, these planets do not pass through every elongation from the sun, as the other planets do. Hence Venus and Mercury are located above the sun by some authorities, like Plato's Timaeus [38 D], but below the sun by others, like Ptolemy [Syntaxis, IX, 1] and many of the modems. Al-Bitruji places Venus above the sun, and Mercury below it.

According to Platos followers, all the planets, being dark bodies otherwise, shine because they receive sunlight. If they were below the sun, therefore, they would undergo no great elongation from it, and hence they would be seen halved or at any rate less than fully round. For, the light which they receive would be reflected mostly upward, that is, toward the sun, as we see in the new or dying moon. In addition, they argue, the sun must sometimes be eclipsed by the interposition of these planets, and its light cut off in proportion to their size. Since this is never observed, these planets do not pass beneath the sun at all, according to those who follow Plato.

On the other hand, those who locate Venus and Mercury below the sun base their reasoning on the wide space which they notice between the sun and the moon. For the moon's greatest distance from the earth is 64 1/6 earth-radii. This is contained, according to them, about 18 times in the sun's least distance from the earth, which is 1160 earth-radii. Therefore between the sun and the moon there are 1096 earth-radii [~ 1160-641/6]. Consequently, to avoid having so vast a space remain empty, they announce that the same numbers almost exactly fill up the apsidal distances, by which they compute the thickness of those spheres. Thus the moon's apogee is followed by Mercury's perigee. Mercurys apogee is succeeded by the perigee of Venus, whose apogee, finally, almost reaches the sun's perigee. For between the apsides of Mercury they calculate about 177 1/2 earthradii. Then the remaining space is very nearly filled by Venus' interval of 910 earth-radii.

Therefore they do not admit that these heavenly bodies have any opacity like the moon's. On the contrary, these shine either with their own light or with the sunlight absorbed throughout their bodies. Moreover, they do not eclipse the sun, because it rarely happens that they interfere with our view of the sun, since they generally deviate in latitude. Besides, they are tiny bodies in comparison with the sun. Venus, although bigger than Mercury, can occult barely a hundredth of the sun. So says Al-Battani of Raqqa, who thinks that the sun's diameter is ten times larger [than Venus'], and therefore so minute a speck is not easily descried in the most brilliant light. Yet in his Paraphrase of Ptolemy, Ibn Rushd reports having seen something blackish when he found a conjunction of the sun and Mercury indicated in the tables. And thus these two planets are judged to be moving below the sun's sphere.

But this reasoning also is weak and unreliable. This is obvious from the fact that there are 38 earth-radii to the moon's perigee, according to Ptolemy [Syntaxis, V, 13], but more than 49 according to a more accurate determination, as will be made clear below. Yet so great a space contains, as we know, nothing but air and, if you please, also what is called "the element of fire". Moreover, the diameter of Venus' epicycle which carries it 45° more or less to either side of the sun, must be six times longer than the line drawn from the earth's center to Venus' perigee, as will be demonstrated in the proper place [V, 21]. In this entire space which would be taken up by that huge epicycle of Venus and which, moreover, is so much bigger than what would accommodate the earth, air, aether, moon, and Mercury, what will they say is contained if Venus revolved around a motionless earth?

Ptolemy [Syntaxis, IX, 1] argues also that the sun must move in the middle between the planets which show every elongation from it and those which do not. This argument carries no conviction because its error is revealed by the fact that the moon too shows every elongation from the sun.

Now there are those who locate Venus and then Mercury below the sun, or Separate these planets [from the sun] in some other sequence. What reason will they adduce to explain why Venus and Mercury do not likewise traverse separate orbits divergent from the sun, like the other planets, without violating the arrangement [of the planets] in accordance with their [relative] swiftness and slowness? Then one of two alternatives will have to be true. Either the earth is not the center to which the order of the planets and spheres is referred, or there really is no principle of arrangement nor any apparent reason why the highest place belongs to Saturn rather than to Jupiter or any other planet.

In my judgement, therefore, we should not in the least disregard what was 5 familiar to Martianus Capella, the author of an encyclopedia, and to certain other Latin writers. For according to them, Venus and Mercury revolve around the sun as their center. This is the reason, in their opinion, why these planets diverge no farther from the sun than is permitted by the curvature of their revolutions. For they do not encircle the earth, like the other planets, but "have opposite circles". Then what else do these authors mean but that the center of their spheres is near the sun? Thus Mercury's sphere will surely be enclosed within Venus', which by common consent is more than twice as big, and inside that wide region it will occupy a space adequate for itself. If anyone seizes this opportunity to link Saturn, Jupiter, and Mars also to that center, provided he understands their spheres to be so large that together with Venus and Mercury the earth too is enclosed inside and encircled, he will not be mistaken, as is shown by the regular pattern of their motions.

For [these outer planets] are always closest to the earth, as is well known, about the time of their evening rising, that is, when they are in opposition to the 2 sun, with the earth between them and the sun. On the other hand, they are at their farthest from the earth at the time of their evening setting, when they become invisible in the vicinity of the sun, namely, when we have the sun between them and the earth. These facts are enough to show that their center belongs more to the sun, and is identical with the center around which Venus and Mercury likewise execute their revolutions.

But since all these planets are related to a single center, the space between Venus' convex sphere and Mars' concave sphere must be set apart as also a sphere or spherical shell, both of whose surfaces are concentric with those spheres. This [intercalated sphere] receives the earth together with its attendant, 3 the moon, and whatever is contained within the moon's sphere. Mainly for the reason that in this space we find quite an appropriate and adequate place for the moon, we can by no means detach it from the earth, since it is incontrovertibly nearest to the earth.

Hence I feel no shame in asserting that this whole region engirdled by the moon, and the center of the earth, traverse this grand circle amid the rest of the planets in an annual revolution around the sun. Near the sun is the center of the universe. Moreover, since the sun remains stationary, whatever appears as a motion of the sun is really due rather to the motion of the earth. In comparison with any other spheres of the planets, the distance from the earth to the sun has a magnitude which is quite appreciable in proportion to those dimensions. But the size of the universe is so great that the distance earth-sun is imperceptible in relation to the sphere of the fixed stars. This should be admitted, I believe, in preference to perplexing the mind with an almost infinite multitude of spheres, as must be done by those who kept the earth in the middle of the universe. On the contrary, we should rather heed the wisdom of nature. Just as it especially avoids producing anything superfluous or useless, so it frequently prefers to endow a single thing with many effects.

All these statements are difficult and almost inconceivable, being of course opposed to the beliefs of many people. Yet, as we proceed, with God's help I shall make them clearer than sunlight, at any rate to those who arc not unacquainted with the science of astronomy. 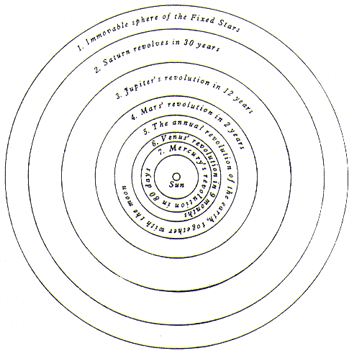Consequently, with the first principle remaining intact, for nobody will propound a more suitable principle than that the size of the spheres is measured by the length of the time, the order of the spheres is the following, beginning with the highest.

The first and the highest of all is the sphere of the fixed stars, which contains itself and everything, and is therefore immovable. It is unquestionably the place of the universe, to which the motion and position of all the other heavenly bodies are compared. Some people think that it also shifts in some way. A different explanation of why this appears to be so will be adduced in my discussion of the earth's motion [I, 11].

[The sphere of the fixed stars] is followed by the first of the planets, Saturn, which completes its circuit in 30 years. After Saturn, Jupiter accomplishes its revolution in 12 years. Then Mars revolves in 2 years. The annual revolution takes the series' fourth place, which contains the earth, as I said [earlier in I, 10], together with the lunar sphere as an epicycle. In the fifth place Venus returns in 9 months. Lastly, the sixth place is held by Mercury, which revolves in a period of 80 days.

At rest, however, in the middle of everything is the sun. For in this most beautiful temple, who would place this lamp in another or better position than that from which it can light up the whole thing at the same time? For, the sun is not inappropriately called by some people the lantern of the universe, its mind by others, and its ruler by still others. [Hermes] the Thrice Greatest labels it a visible god, and Sophocles' Electra, the all-seeing. Thus indeed, as though seated on a royal throne, the sun governs the family of planets revolving around it. Moreover, the earth is not deprived of the moon's attendance. On the contrary, as Aristotle says in a work on animal , the moon has the closest kinship with the earth. Meanwhile the earth has intercourse with the sun, and is impregnated for its yearly parturition.

In this arrangement, therefore, we discover a marvelous symmetry of the universe, and an established harmonious linkage between the motion of the spheres and their size, such as can be found in no other way. For this permits a not inattentive student to perceive why the forward and backward arcs appear greater in Jupiter than in Saturn and smaller than in Mars, and on the other hand greater in Venus than in Mercury. This reversal in direction appears more frequently in Saturn than in Jupiter, and also more rarely in Mars and Venus than in Mercury. Moreover, when Saturn, Jupiter, and Mars rise at sunset, they are nearer to the earth than when they set in the evening or appear at a later hour. But Mars in particular, when it shines all night, seems to equal Jupiter in size, being distinguished only by its reddish color. Yet in the other configurations it is found barely among the stars of the second magnitude, being recognized by those who track it with assiduous observations. All these phenomena proceed from the same cause, which is in the earth's motion.

Yet none of these phenomena appears in the fixed stars. This proves their immense height, which makes even the sphere of the annual motion, or its reflection, vanish from before our eyes. For, every visible object has some measure of distance beyond which it is no longer seen, as is demonstrated in optics. From Saturn, the highest of the planets, to the sphere of the fixed stars there is an additional gap of the largest size. This is shown by the twinkling lights of the stars. By this token in particular they are distinguished from the planets, for there had to be a very great difference between what moves and what does not move. So vast, without any question, is the divine handiwork of the most excellent Almighty.

PROOF OF THE EARTH'S TRIPLE MOTION    Chapter 11

In so many and such important ways, then, do the planets bear witness to the earth's mobility. I shall now give a summary of this motion, insofar as the phenomena are explained by it as a principle. As a whole, it must be admitted to be a threefold motion.

The first motion, named nuchthemeron by the Greeks, as I said [I, 4], is the rotation which is the characteristic of a day plus a night. This turns around the earth's aids from west to east, just as the universe is deemed to be carried in the opposite direction. It describes the equator, which some people call the "circle of equal days", in imitation of the designation used by the Greeks, whose term for it is isemerinos.

The second is the yearly motion of the center, which traces the ecliptic around the sun. Its direction is likewise from west to east, that is, in the order of the zodiacal signs. It travels between Venus and Mars, as I mentioned [I, 10], together with its associates. Because of it, the sun seems to move through the zodiac in a similar motion. Thus, for example, when the earth's center is passing through the Goat, the sun appears to be traversing the Crab; with the earth in the Water Bearer, the sun seems to be in the Lion, and so on, as I remarked.

To this circle, which goes through the middle of the signs, and to its plane, the equator and the earth's axis must be understood to have a variable inclination. For if they stayed at a constant angle, and were affected exclusively by the motion of the center, no inequality of days and nights would be observed. On the contrary, it would always be either the longest or shortest day or the day of equal daylight and darkness, or summer or winter, or whatever the character of the season, it would remain identical and unchanged.

The third motion in inclination is consequently required. This also is a yearly revolution, but it occurs in the reverse order of the signs, that is, in the direction opposite to that of the motion of the center. These two motions are opposite in direction and nearly equal in period. The result is that the earth's axis and equator, the largest of the parallels of latitude on it, face almost the same portion of the heavens, just as if they remained motionless. Meanwhile the sun seems to move through the obliquity of the ecliptic with the motion of the earth's center, as though this were the center of the universe. Only remember that, in relation to the sphere of the fixed stars, the distance between the sun and the earth vanishes from our sight forthwith.

Since these are matters which crave to be set before our eyes rather than spoken of, let us describe a circle ABCD, which the annual revolution of the earth's center has traced in the plane of the ecliptic. Near its center let the sun be E. I shall divide this circle into four parts by drawing the diameters AEC and BED. Let A represent the first point of the Crab, B of the Balance, C of the Goat, and D of the Ram. Now let us assume that the earth's center is originally at A. About A I shall draw the terrestrial equator FGHI. This is not in the same plane [as the ecliptic], except that the diameter GAI is the intersection of the circles, I mean, of the equator and the ecliptic. Draw also the diameter FAH perpendicular to GAI, F being the limit of the [equator's] greatest inclination to the south, and H to the north. Under the conditions thus set forth, the earth's inhabitants will see the sun near the center E undergo the winter solstice in the Goat. This occurs because the greatest northward inclination, H, is turned toward the sun. For, the inclination of the equator to the line AE, through the agency of the daily rotation, traces the winter solstice parallel to the equator at an interval subtended by EAH, the angle of the obliquity.

Now let the earth's center start out in the order of the signs, and let F, the limit of maximum inclination, travel along an equal arc in the reverse order of the signs, until at B both have traversed a quadrant of their circles. In the interim the angle EAI always remain equal to AEB, on account of the equality of their revolutions; and the diameters always stay parallel to each other, FAH to FBH, and GAI to GBI, and the equator to the equator. In the immensity of the heavens, for the reason already frequently mentioned, the same phenomena appear. Terefore from B, the first point of the Balance, E will seem to be in the Ram. The intersection of the circles will coincide with the single line GBIE, from which [the plane of the axis] win not be permitted by the daily rotation to deviate. On the contrary, the [axis'] inclination will lie entirely in the lateral plane. Accordingly the sun will be seen in the spring equinox. Let the earth's center proceed under the assumed conditions, and when it has completed a semicircle at C, the sun will appear to enter the Crab. But F, the southernmost inclination of the equator, will be turned toward the sun. This will be made to appear in the north, undergoing the summer solstice as measured by the angle of the obliquity, ECR Again, when F turns away in the third quadrant of the circle, the intersection GI will once more fall on the line ED. From here the sun will be seen in the Balance undergoing the autumn equinox. Then as H by the same process gradually faces the sun, it will bring about a repetition of the initial situation, with which I began my survey

Alternatively, let AEC be in the same way a diameter of the plane under discussion [the ecliptic] as well as the intersection of that plane with a circle perpendicular thereto. On AEC, around A and C, that is, in the Crab and the Goat, draw a circle of the earth in each case through the poles. Let this [meridian] be DGFI, the earth's axis DF, the north pole D, the south pole F, and GI the diameter of the equator. Now when F is turned toward the sun, which is near E, the equator's northward inclination being measured by the angle IAE, then the axial rotation will describe, parallel to the equator and to the south of it, at a distance LI and with diameter KL, the tropic of Capricorn as seen in the sun. Or, to speak more accurately, the axial rotation, as viewed from AE, generates a conic surface, having its vertex in the center of the earth, and its base in a circle parallel to the equator. Also at the opposite point, C, everything works out in like manner, but is reversed. It is clear therefore how the two motions, I mean, the motion of the center and the motion in inclination, by their combined effect make the earth's axis remain in the same direction and in very much the same position, and make all these phenomena appear as though they were motions of the sun.

I said, however, that the annual revolutions of the center and of inclination are nearly equal. For if they were exactly equal, the equinoctial and solstitial points as well as the entire obliquity of the ecliptic would have to show no shift at all with reference to the sphere of the fixed stars. But since there is a slight variation, it was discovered only as it grew larger with the passage of time. From Ptolemy to us the precession of the equinoxes amounts to almost 21°. For this reason some people believed that the sphere of the fixed stars also moves, and accordingly they adopted a surmounting ninth sphere. This having proved inadequate, more recent writers now add on a tenth sphere. Yet they do not in the least attain their goal, which I hope to reach by the earth's motion. This I shall use as a principle and hypothesis in the demonstration of the other [motions].

[Here Copernicus originally planned to include a little time than two handwritten pages which he later deleted from his autograph. This deleted material, which was not printed in the first four editions of the Revolutions (1543, 1566, 1617, 1854), but was incorporated in those published after the recovery of Copernicus' autograph (1873, 1949, 1972), reads as follows].

The proofs which I shall use in almost the entire work involve straight lines and arcs in plane and spherical triangles. Although much information about these topics is already available in Euclid's Elements, nevertheless that treatise does not contain the answer to what is the principal question here, how the sides can be obtained from the angles, and the angles from the sides.

[As the heading of 1, 12, the first edition introduced "The Length of Straight Lines in a Circle". This caption, for which there is no direct warrant in the autograph, was repeated in the next three editions of the Revolutions.

HOW MUCH ARE THE ORBITS OF SATURN,     Chapter 3
JUPITER, AND MARS INCLINED?

Having explained the theory of the latitudes of the five planets, I must now turn to the facts and analyze the details. First [I must determine] how much the individual circles are inclined. We compute these inclinations by means of the great circle which passes through the poles of the inclined circle at right angles to the ecliptic. On this great circle the deviations in latitude are determined. When these arrangements are understood, the road will be open to ascertaining the latitudes of each planet.

Once more let us begin with the three outer planets. At their farthest southern limits of latitude, as shown in Ptolemy's Table [Syntaxis, XIII, 5], when they are in opposition, Saturn deviates 3° 5', Jupiter 2° 7' and Mars 7° 7'. On the other hand, in the opposite places, that is, when they are in conjunction with the sun, Saturn deviates 2° 2', Jupiter 1° 5', and Mars only 5', so that it almost grazes the ecliptic. These values could be inferred from the latitudes observed by Ptolemy around the time of the planets' disappearances and first visibilities.

Now that the above assertions have been set forth, let a plane perpendicular to the ecliptic pass through its center and intersect the ecliptic in AB. But let its intersection with the eccentric of any of the three outer planets be CD, passing through the farthest southern and northern limits. Let the ecliptic's center be E; the diameter of the earth's grand circle, FEG; the southern latitude, D; and the northern, C. Join CF, CG, DF, and DG.

[Earlier version:

Now as an example I shall use Mars because it exceeds all the other planets in latitude. Thus, when it is in opposition at point D, with the earth at G (corrected from F], angle AFG was known = 7° 7'. But 0 is given as Mars' position at apogee. From the previously established sizes of the circle, CE = 1° 22'20", with FG [a slip for FE] = 1°. In triangle CEF, the ratio of the sides GE and EF is given, as well as angle CFE. Hence we shall also have as given CEF = the greatest angle of the eccentric's inclination = 5° 11', according to the doctrine of plane triangles. However, when the earth is in the opposite place, that is, at G (should have been corrected to F], while the Planet is still at C, CGF = the angle of the apparent latitude = 4'].

[Printed version:

For each planet the ratio of EG, (the radius] of the earth's grand circle, to ED, [the radius] of the planet's eccentric, has already been shown above for any given places of earth and planet. But the places of the maximum latitudes are also given by observation. Therefore BGD, the angle of the greatest southern latitude, is given as an exterior angle of triangle EGD. In accordance with the theorems on Plane Triangles, the opposite interior angle GED will also be given as the angle of the eccentric's maximum southern inclination to the plane of the ecliptic. By means of the minimum southern latitude we shall likewise demonstrate the mm inclination, for example, by mean of angle EFD. In triangle EFD, the ratio of sides EF : ED is given as well as angle EFD. Therefore we shall, have exterior GED given as the angle of the minimum southern inclination. Accordingly, from the difference between both inclinations we shall obtain the whole oscillation of the eccentric in relation to the ecliptic. Furthermore, by means of these angles of inclination we shall compute the opposite northern latitudes, such as AFC and EGC. If these agree with the observations, they Will indicate that we have made no error.

However, as an example I shall use Mars, because it exceeds all the other planets in latitude. Its maximum southern latitude was noted by Ptolemy as about 7° when Mars was at perigee, and its maximum northern latitude at apogee as 4° 20' [Syntaxis, XIII, 5]. However, having determined angle BGD = 6° 50', I found the corresponding angle AFC ~ 4° 30'. Given EG : ED = 1p : 1p 22' 26" [V, 19], from these sides and angle BGD we shall obtain angle DEG of the maximum Southern inclination ~ 1° 51'. Since EF : CE = 19 : 1° 39' 57" [V, 19] and angle CEF = DEG = 1° 51', consequently the aforementioned exterior CFA = 4 1/2° when the planet is in opposition.

Similarly , at the opposite place when it is in conjunction with the sun, suppose that we assume angle DFE = 5'. From the given sides DE and EF together with angle EFD, we shall obtain angle EDF, and exterior angle DEG of the inclination ~ 9'. This will furnish us also with angle CGE of the northern latitude ~ 6'. Hence, if we subtract the minimum inclination from the maximum, that is, 1° 51'-9', the remainder ~ 1° 41'. This is the oscillation of this inclination, and 1/2 [of the oscillation] ~ 50 1/2'.

In like manner the angles of inclination of the other two planets, Jupiter and Saturn, were determined together with their latitudes. Thus, Jupiter's maximum inclination = 1° 42'; its minimum inclination = 1° 18'; hence, its entire oscillation comprises not more than 24'. On the other hand, Saturn's maximum inclnation = 2° 44'; its minimum inclination = 2° 16'; the intervening oscillation = 28'. Hence, through the smallest angles of inclination, which occur in the opposite place, when the planets are in conjunction with the sun, their deviations in latitude from the ecliptic will emerge as 2° 3' for Saturn and 1° 6' for Jupiter. These values had to be determined and retained for the construction of the Tables below [after VI, 8].

GENERAL EXPLANATION OF ANY OTHER     Chapter 4
LATITUDES OF THESE THREE PLANETS

From what has been expounded above, the particular latitudes of these three planets will likewise be clear in general. As before, conceive the intersection AB of the plane perpendicular to the ecliptic and passing through the limits of their farthest deviations, with the northern limit at A. Also let straight line CD be the intersection of the planet's orbit [with the ecliptic], and let CD intersect AB in point D. With D as cemer, describe EF as the earth's grand circle. From E, where the earth is allgued with the planet in opposition, take any known arc EF. From F and from Q, the place of the planet, drop CA and FG perpendicular to AB. Join FA and FC.

In this situation we first seek the size of ADC, the angle of the eccentric's inclination. It has been shown [VI, 3] to be at its maximum when the earth is in point E. Its entire oscillation, moreover, as is required by the oscillation's nature, was revealed to be commensurate with the earth's revolution on circle EF, as determined by diameter BE. Therefore, because arc EF is given, ratio ED : EG will be given, and this is the ratio of the entire oscillation to that which was just detached from angle ADC Hence in the present situation angle ADC is given.

Consequently, in triangle ADC, the angles being given, all its sides are given. But ratio CD : ED is given by the foregoing. Also given, therefore, is [the ratio of CD] to DG, the remainder [when EG is subtracted from ED]. Consequently the ratios of both CD and AD to GD are known. Accordingly, AG, the remainder [when GD is subtracted from AD], is also given. From this information FG is likewise given, since it is half of the chord subtending twice EF. Therefore, in right triangle AGF, two sides [AG and FG] being given, hypotenuse AF is given, and so is ratio AF: AG. Thus, finally, in right triangle ACF, two sides [AF and AC] being given, angle AFC will be given, and this is the angle of the apparent latitude, which was sought.

Again I shall exemplify this analysis with Mars. Let its maximum limit of southern latitude, which occurs near its lower apse, be in the vicinity of A. How ever, let the place of the planet be C where ADC, the angle of the inclination, was shown [VI, 3] to be at its maximum, namely, 1° 50', when the earth was at point E. Now let us put the earth at point F, and the motion in parallax, along arc EF = 450. Therefore, straight line FG is given = 7071p whereof ED = 10,000 p, and GE, the remainder (when GD = FG = 7071p is subtracted] from the radius [= ED = 10,000p] = 2929p. But half of ADC, the angle of the oscillation, has been shown = 0° 50 1/2' [VI, 3]. In this situation its ratio of increase and decrease = DE : GE = 50° 1/2' : 15'. When we subtract this latter quantity from 1° 50', the remainder = 1° 35' = ADC, the angle of the inclination in the present situation. Therefore, the angles and sides of triangle ADC will be given. CD was shown above to be = 9040p whereof ED = 6580p [V, 19]. Hence, in those same units FG = 4653p; AD =9036p; AEG, the remainder [when GD = FG = 4653P is subtracted from AD 9036p] = 4383p, and AC = 249 1/2p. Therefore, in right triangle AFG, perpendicular AG = 4383p, and base FG = 4653p; hence, hypotenuse AF = 6392p. Thus, finally, triangle ACF has CAF as a right angle, together with given sides AC and AF [= 2491/2p, 6392p]. Hence, angle AFC is given = 2° 15' = the apparent latitude when the earth is situated at F. We shall pursue the analysis in the same way for the other two planets, Saturn and Jupiter.

THE LATITUDES OF VENUS-AND MERCURY    Chapter 5

Venus and Mercury remain. Their deviations in latitude, as I said [VI, 1], win be demonstrated jointly by three interrelated latitudinal excursions. In order to be able to separate these from one another, I shall begin with the one called the "declination", since it is simpler to treat. It is the only one which sometimes happens to be separated from the others. This [separation occurs] near the middle longitudes and near the nodes when, as reckoned by the corrected motions in longitude, the earth is located a quadrant's distance from the planet's apogee and perigee. When the earth is near the planet, [the ancients] found 6° 22' of southern or northern latitude in Venus, and 4° 5' in Mercury; but with the earth at its greatest distance [from the planet], 1° 2' in Venus, and 1° 45'in Mercury [Ptolemy, Syntaxis, XIII, 5]. Under these circumstances the planets' angles of inclination are made known through the established tables of corrections [after VI, 8]. Therein, when Venus is at its greatest distance from the earth with its latitude = 1° 2, and at its least distance [from the earth with its latitude =] 6° 22', an arc of approximately 2 1/2° of orbital [inclination] fits both cases. When Mercury is most remote (from the earth], its latitude = 1° 45', and when it is closest [to the earth, its latitude =] 4° 5' require an arc of 6 1/4° [as the inclination] of its orbit. Hence, the orbits' angles of inclination = 2° 30' for Venus, but for Mercury 6 1/4°, with 360° = 4 right angles. Under these circumstances each of their particular latitudes in declination can be explained, as I shall presently demonstrate, and first for Venus.

Let the ecliptic be the plane of reference. Let a plane perpendicular to it and passing through its center intersect it in ABC. Let (the ecliptic's] intersection with Venus, orbital plane be DBE. Let the earth's center be A; the center of the a planet's orbit, B; and the angle of the orbit's inclination to the ecliptic, ABE. With B as center, describe orbit DFEG. Draw diameter FBG perpendicular to diameter DE. Let the orbit's plane be conceived to be so related to the assumed perpendicular plane that lines drawn therein perpendicular to DE are parallel to one another and to the plane of the ecliptic, in which FBG is the only [such perpendicular].

From the given straight lines AB and BC, together with ABE, the given angle of inclination, it is proposed to find how much the planet deviates in latitude. Thus, for example, let the planet be at a distance of 45° away from E, the point nearest to the earth. Following Ptolemy [Syntaxis, XIII, 4], I have chosen this point in order that it may be clear whether the inclination of the orbit produces any variation in the longitude of Venus or Mercury. For, such variations would have to be seen at their maximum about halfway between the cardinal points D, F, E, and G. The principal reason therefor is that when the planet is located at these four cardinal points, it experiences the same longitudes as it would have without any declination, as is self-evident.

Therefore, let us take arc EH = 45° as was said. Drop HK perpendicular to BE. Draw KL and HM perpendicular to the ecliptic as the plane of reference. Join HB, LM, AM, and AH. We shall have LKHM as a parallelogram with 4 right angles, since HK is parallel to the plane of the ecliptic [KL and HM having been drawn perpendicular to the ecliptic]. The side [LM of the parallelogram] is enclosed by LAM, the angle of the longitudinal prosthaphaeresis. But angle HAM embraces the deviation in latitude, since HM also falls perpendicularly on the same plane of the ecliptic. Angle HBE is given = 45'. Therefore, HK = half the chord subtending twice HE = 7071p whereof EB = 10,000p.

Similarly, in triangle BKL, angle KBL is given = 2° 1/2' [VI, 5, above], ELK is a right angle, and hypotenuse BK= 7071p whereof BE = 10,000p. In the same units, the remaining sides KL = 308p and BL = 7064p. But, as was shown above [V, 21], AB : BE ~10,000p : 7193p. In the same units, therefore, the remaining sides HK = 5086p; HM = KL = 221P; and BL = 5081p. Hence LA, the remainder (when BL = 5081p is subtracted from AB = 10,000p] = 4919p. Now once more, in triangle ALM, sides AL and LM = HK are given [= 4919p, 5086p], and ALM is a right angle. Hence we shall have hypotenuse AM = 7075p, and angle MAL = 45° 57' = Venus' prosthaphaeresis or great parallax, as computed.

Similarly, in triangle [MAH], side AM is given = 7075p, and side MH = KL [= 221p]. Hence, angle MAH is obtained = 1° 47' = the latitudinal declination. But if it is not boring to consider what variation in longitude is produced by this declination of Venus, let us take triangle ALH, understanding LH to be a diagonal of parallelogram LKHM = 5091p where of AL = 4919p. ALH is a right angle. From this information hypotenuse AH is obtained = 7079p. Hence, the ratio of the sides being given, angle HAL = 45° 59'. But MAL was shown = 45° 57'. Therefore, the excess is only 2'. Q. E. D.

Again, in like manner I shall demonstrate the latitudes of declination in Mercury by a construction similar to the foregoing. Therein assume arc EH = 45° so that each of the straight lines HK and KB is taken, as before, = 7071p whereof hypotenuse HB = 10,000p. In this situation, as can be inferred from the differences in longitude as shown above [V, 27], radius BH = 3953p and AB = 9964 p. In such units, BK and KH will both be = 2795p. ABE, the angle of inclination, was shown [VI, 5, above] = 6° 15', with 360° = 4 right angles. Hence, in right triangle BKL the angles are given. Accordingly, in the same units base KL = 304p, and the perpendicular BL = 2778p. Therefore, AL, the remainder (when BL = 2778p is subtracted from AB = 9964p) = 7186p. But LM = HK = 2795p. Hence, in triangle ALM, L is a right angle, and two sides, AL and LM, are given [= 7186p, 2795p]. Consequently, we shall have hypotenuse AM = 7710p, and angle LAM = 21° 16' = the computed prosthaphaeresis.

Similarly, in triangle AMH, two sides are given: AM [= 7710p], and MH = KL [= 304p], forming right angle M. Hence, angle MAH is obtained = 2° 16' = the latitude we were seeking. It may be asked how much [of the latitude] is owing to the true and apparent prosthaphaeresis. Take LH, the diagonal of the parallelogram. From the sides we obtain it = 2811p, and AL = 7186p. These show angle LAH = 21° 23' = the apparent prosthaphaeresis. This exceeds the previous calculation [of angle LAM = 21° 16'] by about 7'. Q. E. D.

VENUS' AND MERCURYS SECOND    Chapter 6
LATITUDINAL DIGRESSION, DEPENDING
ON TBE INCLINATION OF TBEIR
ORBITS AT APOGEE AND PERIGEE

The foregoing remarks concerned that latitudinal digression of these planets which occurs near the middle longitudes of their orbits. These latitudes, as I said [VI, 1], are called the "declinations". Now I must discuss the latitudes which happen near the perigees and apogees. With these latitudes is mingled the deviation or third [latitudinal] digression. Such a deviation does not occur in the three outer planets, but [in Venus and Mercury] it can more easily be distinguished and separated out in thought, as follows.

Ptolemy observed [Syntaxis, XIII, 4] that these (perigeal and apogeal] latitudes appeared at their maximum when the planets were on the straight lines drawn from the center of the earth tangent to their orbits. This happens, as I said [V, 21, 27], when the planets are at their greatest distances from the sun in the morning and evening. Ptolemy also found [Syntaxis, XIII, 3] that Venus' northem latitudes were 1/3° greater than the southern, but Mercury's southern latitudes were about 11/2° greater than the northern. However, out of a desire to take into account the difficulty and labor of the computations, he accepted 21/2° as a sort of average quantity for the varying values of the latitude, mainly because he believed that no perceptible error would thereby arise, as I too shall soon show [VI, 7]. These degrees are subtended by the latitudes on the circle around the earth and at right angles to the ecliptic, the circle on which the latitudes are measured. If we now take 21/2° as the equal digression to either side of the ecliptic and for the time being exclude the deviation, our demonstrations will be simpler and easier until we have ascertained the latitudes of the obliquations.

Then we must first show that this latitude's digression reaches its near the eccentric's point of tangency, where the longitudinal prosthaphaereses are also at their peak. Let the planes of the ecliptic and the eccentric, whether Venus' or Mercury's, intersect [in a line] through the [planet's] apogee and perigee. On the intersection take A as the place of the earth, and B as the center of the eccentric circle CDEFG, which is inclined to the ecliptic. Hence, [in the eccentric] any straight lines drawn perpendicular to CG form angles equal to the inclination [of the eccentric to the ecliptic]. Draw AR tangent to the eccentric, and AFD as any secant. From points D, E, and F, furthermore, drop DH, EK, and FL Perpendicular to CQ; and also DM, EN, and FO perpendicular to the horizontal plane of the ecliptic. Join MH, NK, and OL, as well as AN and AOM. For, AOM is a straight line, since three of its points are in two planes, namely, the plane of the ecliptic, and the plane ADM perpendicular to the plane of the ecliptic. For the assumed inclination, then, angles HAM and KAN enclose the longitudinal prosthaphaereses of these planets, whereas their digressions in latitude are embraced by angles DAM and EAN.

I say, first, that the greatest of all the latitudinal angles is EAN, which is formed at the point of tangency, where the longitudinal prosthaphaeresis also is nearly at its maximum. For, angle EAK is the greatest of all [the longitudinal angles]. Therefore RE: EA > HD : DA and LF : FA. But EK : EN = RD : DM = LF : FO, since the angles subtended (by the second members of these ratios) are equal, as I said. Moreover, M, N, and O are right angles. Consequently, NE : EA > AW : DA and OF : FA. Once more, DMA, ENA, and FOA are light angles. Therefore, angle EAN is greater than DAM and all the [other] angles which are formed in tins way.

Of the difference in longitudinal prosthaphaeresis caused by this obliquation, consequently, clearly the maximum is also that which occurs at the greatest elongation near point B. For on account of the equality of the angles subtended [in the similar triangles], HD : HM = KE : KY = LF : LO. The same ratio holds good for their differences [HD - HM, KE - KN, LF - LO]. Consequently, the difference EK-KN has a greater ratio to EA than the remaining differences have to sides like AD. Hence it is also clear that the ratio of the greatest longitudinal 25 Prosthaphaeresis to the maximum latitudinal digression will be the same as the ratio of the longitudinal prosthaphaereses of segments of the eccentric to the latitudinal digressions. For, the ratio of KE to EN is equal to the ratio of all the sides like LF and RD to the sides like FO and DM. Q. E. D.

THE SIZE OF THE OBLIQUATION ANGLES    Chapter 7
OF BOTH PLANETS, VENUS AND MERCURY

Having made the foregoing preliminary remarks, let us see how great an angle is contained in the inclination of the planes of both these planets. Let us recall what was said above [VI, 5], that each of the planets, when [midway] between its greatest and least distances [from the sun], becomes farther north or south at the most by 5° in opposite directions depending on its position in its orbit. For, at the eccentric's apogee and perigee Venus' digression makes a deviation imperceptibly greater or smaller than 5° from which Mercury departs by more or less.

As before, let ABC be the intersection of the ecliptic and the eccentric. Around B as center, describe the planet's orbit inclined to the plane of the ecliptic in the Manner explained [Previously]. From the center of the earth draw straight line AD tangent to the [planets] orbit at point D. From D drop perpendiculars, DF on CBE, and DG on the horizontal plane of the ecliptic. Join BD, FG, and AG. Also assume that in the caw of both planets angle DAG, comprising half of the aforementioned ditference in latitude, = 21/2°, with 4 right angles = 360°. Let it be proposed to find, for both planets, the size of the angle of inclination of the planes, that is, angle DFG.

In the case of the planet Venus, in units whereof the orbit's radius = 7193p, the planet's greatest distance [from the earth], which occurs at the apogee, has been shown = 10,208p, and its least distance, at perigee, = 9792p [V, 21-22 : 10,000±208]. The mean between these values = 10,000p, which I have adopted for the purposes of this demonstration. Ptolemy wanted to take laboriousness into account and, as far as possible, seek out short cuts [Syntaxis, XIII, 3, end]. For where the extreme values did not produce a manifest difference, it was better to accept the mean value.

Accordingly, AB : BD = 10,000p : 7193p, and ADB is a right angle. Then we shall have side AD = 6947p in length. Similarly, BA : AD = BD : DF, and we shall have DF = 4997p in length. Again, angle DAG is assumed = 2 1/2° and AGD is a right angle. In triangle [ADG, then], the angles being given, side DG = 303p whereof AD = 6947p. Thus also (in triangle DFG] with two sides, DF and DG, being given [= 4997,303], and DGF a right angle, DFG, the angle of inclination or obliquation, = 3° 29'. The excess of angle DAF over FAG comprises the difference in longitudinal parallax. Then the difference must be derived from the known sizes [of those angles].

It has already been shown that in units whereof DG = 303p, hypotenuse AD = 6947p, and DF = 4997p, and also that (AD)²- (DG)²= (AG)², and (FD)²-(DG)² = (GF)². Then as a length AG is given = 6940p, and FG = 4988p. In units whereof AG = 10,000p, FG = 7187p, and angle FAG = 45° 57'. In whereof AD = 10,000p, DF = 7193p, and angle DAF~ 46°. In the greatest obliquation, therefore, the parallactic prosthaphaeresis is diminished by about 3' [= 46° - 45° 57']. At the middle apse, however, clearly the angle of the inclination between the circles was 2 1/2°. Here, however, it has increased [to 3° 29'] by nearly a whole degree, which was added by that first libratory motion which I mentioned.

For Mercury the demonstration proceeds in the same way. In units whereof the orbit's radius 3573p, the orbit's greatest distance from the earth = 10,948p; its least distance 9052p; and between these values the mean = 10,000p [V, 27]. AB : BD = 10,000p : 3573p. Then (in triangle ABD] we shall have the third side AD = 9340p. AB : AD = BD : DF. Therefore DF = 3337p in length. DAG = the angle of the latitude, is assumed = 2 1/2°. Hence DG = 407p whereof DF = 3337p. Thus in triangle DFG, with the ratio of these two sides being given, and with G a right angle, we shall have angle DFG ~ 7°. This is the angle at which Mercury's orbit is inclined or oblique to the plane of the ecliptic. Near the middle longitudes at a quadrant's [distance from apogee and perigee], however, the angle of inclination was shown = 6° 15' [VI, 5]. Therefore, 45' [=7'- 6° 15'] have now been added by the motion of the first libration.

Similarly, for the purpose of ascertaining the angles of prosthaphaeresis and their difference, it may be noticed that straight line DG has be= shown = 407p whereof AD = 9340p and DF = 3337p. (AD)²-(DG)² = (AG)², and (DF)² - (DG)² = (FG)². Then we shall have as a length AG = 9331p, and FG = 3314p. From this information is obtained GAF = the angle of the prosthaphaeresis = 20° 48', whereas DAF = 20° 56', than which GAF, which depends on the obliquation, is about 8' smaller.

It still remains for us to see whether these angles of obliquation and the latitudes connected with the orbit's maximum and minimum distance [from the earth] are found to conform with those obtained by observation. For this purpose in the same diagram again assume, in the first place, for the greatest distance of Venus' orbit [from the earth] that AB : BD = 10,208p : 7193p. Since ADB is a right angle, as a length AD = 7238p in the same units. AB : AD = BD : DF. Then in those units DF = 5102p in length. But DFG = the angle of the obliquity, was found = 3° 29' [earlier in VI, 7]. The remaining side DG = 309p whereof AD = 7238p. Then, in units whereof AD = 10,000p, DG = 427p. Hence, angle DAG is inferred = 2° 27' at the [planet's] greatest distance from the earth. However, in units whereof BD = the orbit's radius = 7193p, AB = 9792p [= 10,000-208] at the [planet's] least [distance from the earth]. AD, perpendicular to BD, = 6644p. AB : AD = BD : DF. Similarly, as a length DF is given = 4883p in those units. But angle DFG has been put = 3° 29'. Therefore, DG is given = 297p whereof AD = 6644p. Consequently in triangle [ADG], the sides being given, angle DAG is given= 2° 34'. However, neither 3' nor 4' [2° 30' = 3'+2° 27' = 2° 34'-4'] are large enough to be registered instrumentally with the aid of astrolabes. Hence, what was regarded as the maximum latitudinal digression in the planet Venus stands up well.

In like manner assume that the greatest distance of Mercury's orbit [from the earth is to the radius of Mercury's orbit], that is, AB : BD = 101948p :3573p [V, 27]. Thus, by demonstrations like the foregoing, we obtain AD = 9452p, and DF = 3085p. But here again we have DFG, the angle of the inclination [between Mercury's orbit and the plane of the ecliptic] known = 7° and for that reason straight line DG = 376p whereof DF = 3085p or DA = 9452p. Hence in right triangle DAG, whose sides are given, we shall have angle DAG ~ 2° 17' = the greatest digression in latitude.

At the [orbits] least distance [from the earth], however, AB : BD is put = 9052p :3573p. Hence, in those units AD = 8317p, and DF = 3283p. However, on account of the same inclination [ = 7°] DF : DG is put = 3283p : 400p whereof AD = 8317p. Hence, angle DAG = 2°45'.

The latitudinal digression associated with the mean value [of the distance of Mercury's orbit from the earth) is here too assumed = 2 1/2°. From this quantity the latitudinal digression at apogee, where it reaches its minimum, differs by 13' [=2° 30'- 2° 17']. At perigee, however, where the latitudinal digression attains its maximum, it differs (from the mean value] by 15' [= 2°45'-2° 30']. Instead of these [apogeal and perigeal differences], in computations based on the mean value, above it and below it I shall use 1/4°, which does not differ perceptibly from the observations.

As a result of the foregoing demonstrations, and also because the greatest longitudinal prosthaphaereses have the same ratio to the greatest latitudinal digression as the partial prosthaphaereses in the remaining portions of the orbit have to the several latitudinal digressions, we shall obtain all the latitudinal quantities occurring on account of the inclination of the orbits of Venus and Mercury. But only the latitudes midway between apogee and perigee, as I said [VI, 5], are available. It has been shown that of these latitudes the maximum 21/2° [VI, 6], while Venus' greatest prosthaphaeresis = 46°, and Mercury's ~ 22° [VI, 5 : 45° 57', 21° 16']. And now in the tables of their nonuniform motions [after V, 33] we have the prosthaphacreses alongside the individual portions of the orbits. To the extent that each of the prosthaphacreses is smaller than the maximum, I shall take the corresponding part of those 2 1/2° for each planet. I shall record that part numerically in the Table which is to be set out below [after VI, 8]. In this way we shall have in detail every individual latitude of obliquation which occurs when the earth is at the higher and lower apsides of these planets. In like manner I have recorded the latitudes of their declinations [when the earth is] at a quadrant's distance (midway between the planets' apogee and perigee], and Me planets are] at their middle longitudes. What occurs between these four critical points [higher, lower, and both middle apsides] can be derived by the subtlety of the mathematical art from the proposed system of circles, not without labor, however. Yet Ptolemy was everywhere as compact as possible. He recognized [Syntaxis, XIII, 4, end] that by themselves both of these kinds of latitude [declination, obliquation] as a whole and in all their parts increased and decreased pro portionally like the moon's latitude. He therefore multiplied each of their parts by twelve, since their maximum latitude = 5° = 1/12 x 60°. He made these [products] into proportional minutes, which he thought should be used not only in these two planets but also in the three outer planets, as will be explained below [VI, 9].