


Next: About this document ...
Chance
October 20, 2000
Let
be a random quantity determined by some experiment
with expected value denoted
and standard deviation given by
For today, c will denote a positive number. In lecture
we explored (and in X-session proved) the following fact:
FACT 1: The probability that
X is within c units of its expected value is
greater than or equal to
The Fundamental Mysteries of Probability
are that
and that if 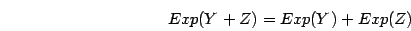 and
and 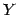 are not dependent on each other, then
are not dependent on each other, then
These mysteries, the above fact, and
the less mysterious facts that
and
give us the
following fact:
FACT 2: Assuming each
is an independent run of
the X experiment, then the
We also will explore today the following fact:
FACT 3:
X is a
heads or tails experiment, then
In class together, we will answer:
- If each
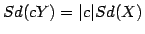 is one with probability
is one with probability 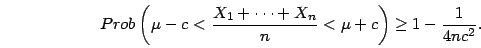 and zero otherwise, how many trials should we perform so
that we can say with 95 percent confidence that the average
and zero otherwise, how many trials should we perform so
that we can say with 95 percent confidence that the average
is within
5 percent of 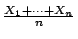 .
.
- If each
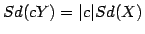 is one with some unknown probability
is one with some unknown probability 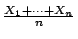 and zero otherwise, how many trials should we perform so
that we can say with 95 percent confidence that the average
and zero otherwise, how many trials should we perform so
that we can say with 95 percent confidence that the average
is within
5 percent of 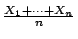 .
.
In groups discuss:
- Discuss how to translate the second and third facts
into English. What are they telling you?
Consider Gallup's poll from October 17 (see handout). To
make the poll a binomial experiment, Gallup considers each outcome
(i.e. Bush more likeable, Gore more likeable, no opinion, etc.) as its
own experiment. For example, to calculate the percentage of people
who see Gore as more likeable, Gallup uses a binomial distribution
where the two outcomes are ``Gore is seen as more likeable'' and
``Gore is not seen as more likeable''.
- 2.
- Using the above facts, with
what confidence should the Gallup
poll have reported that 46 percent of people, with
 error, think
that Gore is more likeable than Bush?
error, think
that Gore is more likeable than Bush?
- 3.
- Suppose that Gallup's claim of 95 percent
confidence with
 percent error can be justified. Notice that the
difference between Bush's percentage and Gore's percentage is two.
With what percent confidence and how much error should we report
concerning this difference?
percent error can be justified. Notice that the
difference between Bush's percentage and Gore's percentage is two.
With what percent confidence and how much error should we report
concerning this difference?
- 4.
- Given your analysis in question 3,
what aspect of Gallup's commentary
is particularly misleading?
Here are your homework and Journal question for this weekend.
- (Homework) Explain why the second fact justifies the
terminology ``expected value''.
- (Homework)
If each
 is
the value we see when rolling a six-sided die one time,
how many trials should we perform so that the average
is
the value we see when rolling a six-sided die one time,
how many trials should we perform so that the average
is within 8 percent of the
expected value of  , with 90 percent confidence.
, with 90 percent confidence.
- (Journal) Articulate the issue arising in question 3, above, and find
another example of an actual poll
(at Gallup or somewhere else) where a misleading
conclusion is presented due to this confusion.



Next: About this document ...
Chance
2000-10-23