| Lecture |
Topics/Sections
|
Some Standard Examples/Concepts
|
|---|
| Day 1 |
2.5 - 2.6
|
Modeling: decay, mixing, cooling, growth. Physical models and the
differential equations which result.
|
| Day 2 |
2.1, 2.2, 2.3, 2.4
|
Review derivation of solution to first order linear, and review separable
equations. Mixing problems (equal rate in/out is separable;
unequal rate is FOL)
|
| Day 3 |
5.2
|
Series solutions to first order linear or second order constant
coefficient. Solve
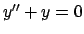 via series, and isolate fundamental
solutions as
via series, and isolate fundamental
solutions as 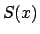 and
and 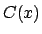 . Observe . Observe 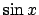 and
and 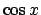 are
also solutions. How are
are
also solutions. How are 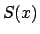 and
and 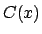 related to
related to 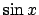 and
and
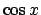 ? Leads to representation of functions by series. ? Leads to representation of functions by series.
|
| Day 4 |
|
Define Taylor polynomials; Define geometric series 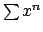 and
show when it converges to the rational function
and
show when it converges to the rational function 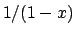 ; Discuss the
notion of Taylor series, and the notion of an
interval of convergence: examples ; Discuss the
notion of Taylor series, and the notion of an
interval of convergence: examples 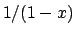 and
and 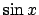 . .
|
| Day 5 |
|
Define 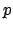 -series and show when they convrge via an improper
integral; state the comparison test and ratio test. Ratio test can
be deduced from the comparison test. Use ration test to define the
radius of convergence of a power series. -series and show when they convrge via an improper
integral; state the comparison test and ratio test. Ratio test can
be deduced from the comparison test. Use ration test to define the
radius of convergence of a power series.
|
| Day 6 |
|
Define the notion of absolute/conditional convergence; Discuss
alternating series and the error resulting from using partial sums.
Consider as an application, the evaluation of (sine, cosine,
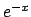 ). How could one build a ). How could one build a 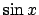 function for a calculator
via partial sums of the Taylor series for the sine?
function for a calculator
via partial sums of the Taylor series for the sine?
|
| Day 7 |
3.1 - 3.3
|
Review of second order constant coefficient (real roots),
Just use characteristic equation
and unmotivated solutions here (proofs in a couple of days)
|
| Day 8 |
3.4
|
Review of complex numbers, complex exponential and second order
constant coefficient (complex roots).
|
| Day 9 |
11.3, 11.4 [Crowell & Slesnick]
|
Linear Differential Operators (formal ring properties).
Homogeneous and nonhomogeneous solutions
Set of homogeneous solutions forms a vector space
General solution of the form 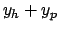
|
| Day 10 |
11.4 [Crowell & Slesnick]
|
Solve second-order constant coefficient problem by reducing to a
first-order system and using general solution to FOL equations.
|
| Day 11 |
4.1, 3.3
|
Linear independence of solutions. General definition.
Theorem 4.12 [4.1] (w/o Wronskian), that is dimension of
space of homog solutions equals the order of the equation.
Detecting linear independence: the Wronskian
Higher dimensional case after a review of determinants
|
| Day 12 |
7.2
|
Review of matrices, determinants (alternating nature)
|
| Day 13 |
4.1
|
Wronskian (higher order): problem 20 page 207
Take an nth order linear DE and write it as a system. Introduce
matrix notation for this motivating Chapter 7. Perhaps revisit Theorem
4.12.
|
| Day 14 |
3.6 3.7
|
[Nonhomogeneous and nonconstant coefficient equations] Finding a
particular solution. Undetermined coefficients and variation of
parameters.
|
| Day 15 |
3.8/7.1
|
Harmonic Oscillators (simple and not)
|
| Day 16 |
7.3
|
Systems of linear equations, linear independence, eigenvalues and
eigenvectors.
|
| Day 17 |
7.3
|
Systems of linear equations, linear independence, eigenvalues and
eigenvectors.
|
| Day 18 |
7.4
|
Basic Theory of First order systems
|
| Day 19 |
7.5
|
Homogeneous linear systems with constant coefficients
|
| Day 20 |
7.6
|
Complex Eigenvalues
|
| Day 21 |
7.7, 10.1
|
Repeated eigenvalues, Separation of Variables (heat conduction)
|
| Day 22 |
10.1
|
Heat equation
|
| Day 23 |
10.2
|
Fourier Series
|
| Day 24 |
10.3, 10.4
|
Fourier Convergence Theorem; Even and odd functions
|
| Day 25 |
10.4, 10.5
|
Even and odd functions; More general heat equation
|
| Day 26 |
10.6
|
The Wave Equation
|
| Day 27 |
10.7
|
Laplace's Equation
|
| Day 28 |
Wrap it up
|
|
| |
|
|
|---|