|
V I E W E R
|
|
i n t e r a c
t i v e d a t a v i s u a l i z a t i o n
t o o l
|
|
by Alex Barnett
|
INTRODUCTION
This is an interactive data viewer built on GLUT
(an interrupt-driven OpenGL/Mesa small application toolkit), written in 1999-2000 in C, and
is completely free software. Please use, enjoy, improve and disseminate!
It is no longer actively supported - contact me if you have trouble.
It was designed for examining sets of many eigenvectors (in my
case real functions of 1 or 2 spatial dimensions, sampled on regular grids),
each with an associated eigenvalue (the eigenvalues together form
a spectrum), emerging from my own research
needs in 2d quantum mechanics. It is currently used by many members of
the Heller Group. It can handle
3 home-grown file formats which are very easy to
write:
1) multiple 1d arrays (ASCII
file)
2) multiple 2d arrays (ASCII
file)
3) multiple 2d arrays (4-byte
floating-point binary file)
It allows perusal of individual eigenvectors or display of all at once.
Brief description of features...
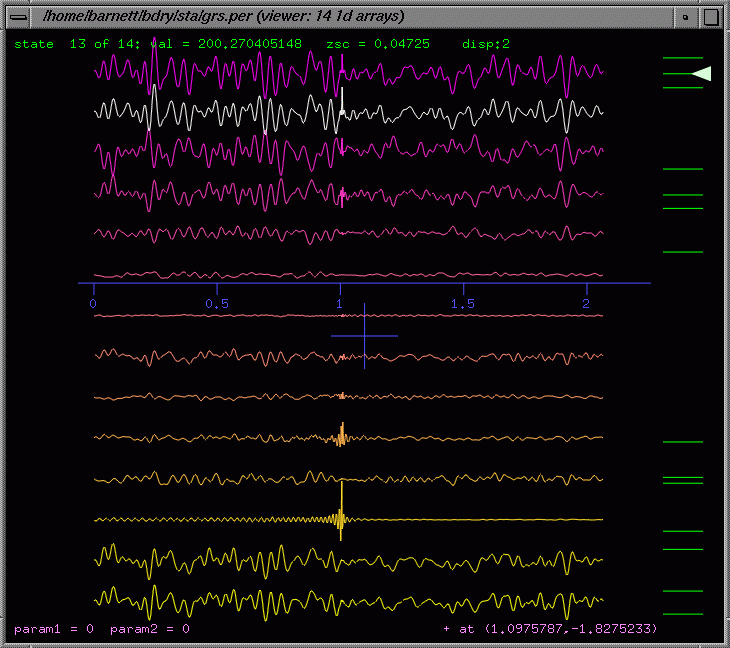 For
1d
data (ie graphs of y(x)), it is modelled on an oscilloscope, allowing
rapid mouse-driven moving, rescaling and read-off of the central cursor
value (bottom right). It also allows all graphs to be compared by displacing
them vertically on the same horizontal axis. Both axes are auto-labelling
in real time. Anti-aliasing and point/lines can be toggled.
For
1d
data (ie graphs of y(x)), it is modelled on an oscilloscope, allowing
rapid mouse-driven moving, rescaling and read-off of the central cursor
value (bottom right). It also allows all graphs to be compared by displacing
them vertically on the same horizontal axis. Both axes are auto-labelling
in real time. Anti-aliasing and point/lines can be toggled.
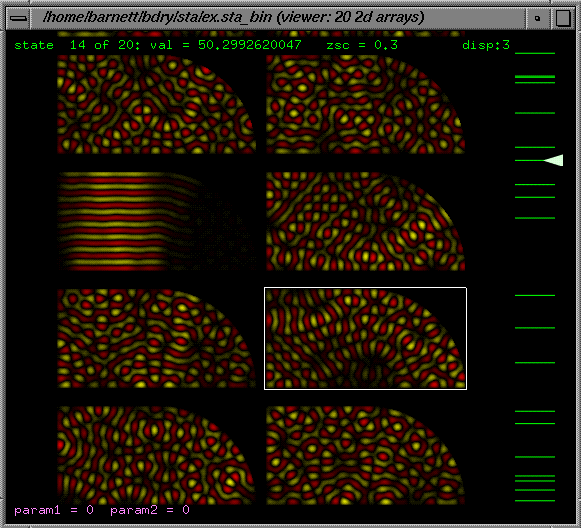
 For
2d
data (ie plots of z(x,y)), individual eigenvectors can be shown as
a surface plot point grid and spun in 3d in a responsive inertial fashion,
or as 2d colour-scale "bit-images" (density plots). The z-scale (contrast)
is adjustable, and there are basic remapping options for z=log(abs(data)),
z=data^2, etc. Also a multiple-image plot is possible. The size of images
is adjustable in units of integer number of pixels per data-point.
For
2d
data (ie plots of z(x,y)), individual eigenvectors can be shown as
a surface plot point grid and spun in 3d in a responsive inertial fashion,
or as 2d colour-scale "bit-images" (density plots). The z-scale (contrast)
is adjustable, and there are basic remapping options for z=log(abs(data)),
z=data^2, etc. Also a multiple-image plot is possible. The size of images
is adjustable in units of integer number of pixels per data-point.
In all cases, the eigenvalue spectrum appears as green bars on a vertical
scale, on the right hand side. Currently this has no axes. The view of
this spectrum is also adjustable, using Shift + mouse buttons.
The Right button gives an embryonic menu, allowing for instance help
to be dumped to the calling window. Pressing the I key gives a dump of
the eigenvalues to the calling window (this could be extended to other
properties).
I believe this interactivity is essential for quick grasp of data. (In
this sense I have been influenced by SciAn,
an excellent but unsupported 3d OpenGL displayer/animator). I hope some
of you can take the small amount of time to write your data in the necessary
format, and reap the rewards of seeing your data as adjustable-contrast
2d images (without resorting to Mathematica or Matlab), or spinning it
around in 3d!
FILE FORMATS
1) Multiple 1d arrays (ASCII file):
<file begins>
d n_samples N x_0 dx
2 param_1 param_2
1 E_1
vector_1_data
2 E_2
vector_2_data
.
.
.
N E_N
vector_N_data
<file ends>
Where...
d = # of dimensions = 1 in this case.
n_samples = how many data samples along the x direction.
N = # eigenvalue/eigenvector pairs, ie the # of states.
x_0 = initial x value (for first data point)
dx = x-spacing between data points. Ie, point i has x_i = x_0 + (i-1)*dx
2 param_1 param_2 = the digit 2 followed by 2 parameters which appear
at
lower left of screen. Currently
only 2 parameters are allowed.
This could easily be changed.
k E_k = state # (k) followed by corresponding k_th eigenvalue. If the
integer k does not match
up with the expected, VIEWER will tell you.
vector_k_data = list of data (y_i) values for k_th 1d array, separated
by spaces. i goes from 1
to n_samples.
See example_data/many1d.sta
2) Multiple 2d arrays (ASCII file):
The differences from format 1) are as follows.
First line now must read:
d n_x_samples n_y_samples N
Where...
d = 2
n_x_samples n_y_samples = # of data points in each direction
N = the # of states, as before
The vector_k_data list now loops over both x and y, with x being the
"fast" direction. In other words, if the data-points are labelled by
integers going from i = 1 to n_x_samples (x direction), and j = 1 to
n_y_samples (y direction), then the data-point (i,j) is to be found
in
the ( (j-1)*n_x_samples + i )_th number in the vector_k_data list.
See example_data/single2d.sta which happens to be a single data set
only (ie N = 1).
3) Multiple 2d arrays (binary file):
This format is a variation of 2), and was designed to handle large
data-sets, being 3-4 times as efficient in terms of storage space.
For this same reason it is also restricted to 4-byte (single-precision)
floats for the vector data. However the eigenvalues are 8-byte doubles.
It also stores the N eigenvector data together at each (i,j) point.
This was optimal for the way the data happened to be generated in my
case.
So now k has become the "fastest" direction:
<file begins>
'b' '*' '*' '*'
N n_x_samples n_y_samples
E_1 ... E_N
vector_data_list
<file ends>
Where...
The opening 4-character sequence must begin with 'b', and the
following 3 are arbitrary. The 'b' identifies the file as a type 3)
data-set (binary multiple 2d).
N n_x_samples n_y_samples = 4-byte integers giving same quantities as
in 2)
E_1 ... E_N = N double-precision (8 byte) eigenvalues
vector_data_list = single-precision (4 byte) floats in binary format.
The difference from 2) is that a sweep over the state # k is
now the "fastest" loop, followed by the "fast" x loop then the "slow"
y loop. This is a triple nested loop. In other words, the data point
(i,j) of state k is found in the vector_data_list at position
((j-1)*n_x_samples + i-1)*N + k. See code for loadstates() if confused.
There are no "space" characters in the file.
There are two choices for the binary format commonly used (IEEE 754):
big- and little- endian, referring to the byte ordering of 4-byte or
8-byte numbers (Most Significant Byte first or Least Significant Byte
first). SGI (mips-IRIX) uses the opposite system to DEC
(alpha-OSF1) and alpha-Linux. Therefore, VIEWER can read both:
if reading fails then append an 'e' argument after the filename and
endian flipping will be done.
See example_data/many2d_binary.sta which is a type 3) multiple data-set
stored using SGI endian ordering. For those of you in the field of quantum
chaos, it happens to be the same stadium eigenstates displayed in Rick
Heller's article on p.627-8 of Les Houches, 1989, however generated in
a few seconds with the method of Vergini & Saraceno.
OTHER NOTES
- PostScript (PS/EPS) multiple 2d image output with labels is now added
(2/27/04). See my poster page for details.
- The limit on total number of data-points is #defined as 1e7 - this can
be enlarged (via recompilation) to whatever your computer can handle.
DOWNLOAD and COMPILATION
Download
the source here (82kb, use tar xvf to expand)
Download
example data here (1.4Mb, use gunzip then tar xvf to expand)
The source directory contains a Makefile for compilation with alpha
Linux systems. GLUT, OpenGL (or Mesa), gcc and the math library must be
already installed (other platform users may need to edit the library names
in the Makefile). The program has been tested only on alpha linux and on
IRIX systems (IRIX requires the change: GLUTLIBS
= -lglut -lGLU -lGL -lXmu -lXext -lX11). It is very simple, consisting
of 3 source files and 3 header files:
viewer.c useful.c nrutils.c
constants.h useful.h nrutils.h
On alpha linux, 4 RPMs are sufficient to provide GLUT and Mesa. I used:
Mesa-3.0-4
Mesa-devel-3.0-4
Mesa-glut-3.0-4
Mesa-glut-devel-3.0-4
These can be found at any RPM web site, for instance this
one. The SGI (IRIX) GLUT library can be found here.
WISH LIST
Read-out of current cursor x,y,z value in 2d data-sets (2d image and 3d
surface plots).
Axes on energy spectrum, axes on 2d images, axes on 3d surface plots.
Postscript output of 1d arrays.
Line and shaded polygon options for 3d surface plots.
Autoranging from input file.
Complex values displayed with phase colour-wheel.
................................... Contact
me
at barnett at cims.nyu.edu ................................
View
this
page in Romanian courtesy of azoft

 For
2d
data (ie plots of z(x,y)), individual eigenvectors can be shown as
a surface plot point grid and spun in 3d in a responsive inertial fashion,
or as 2d colour-scale "bit-images" (density plots). The z-scale (contrast)
is adjustable, and there are basic remapping options for z=log(abs(data)),
z=data^2, etc. Also a multiple-image plot is possible. The size of images
is adjustable in units of integer number of pixels per data-point.
For
2d
data (ie plots of z(x,y)), individual eigenvectors can be shown as
a surface plot point grid and spun in 3d in a responsive inertial fashion,
or as 2d colour-scale "bit-images" (density plots). The z-scale (contrast)
is adjustable, and there are basic remapping options for z=log(abs(data)),
z=data^2, etc. Also a multiple-image plot is possible. The size of images
is adjustable in units of integer number of pixels per data-point.
 For
1d
data (ie graphs of y(x)), it is modelled on an oscilloscope, allowing
rapid mouse-driven moving, rescaling and read-off of the central cursor
value (bottom right). It also allows all graphs to be compared by displacing
them vertically on the same horizontal axis. Both axes are auto-labelling
in real time. Anti-aliasing and point/lines can be toggled.
For
1d
data (ie graphs of y(x)), it is modelled on an oscilloscope, allowing
rapid mouse-driven moving, rescaling and read-off of the central cursor
value (bottom right). It also allows all graphs to be compared by displacing
them vertically on the same horizontal axis. Both axes are auto-labelling
in real time. Anti-aliasing and point/lines can be toggled.