


Next: General potential case
Up: Appendix D: How Many
Previous: Appendix D: How Many
For any
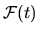 we can define
we can define
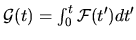 , whose autocorrelation
function
, whose autocorrelation
function
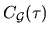 is related to that of
is related to that of 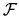 (using the time-average form (2.30)) by
(using the time-average form (2.30)) by
![\begin{displaymath}
C(\tau) \; = \; -\frac{d^2}{d\tau^2} C_{\mathcal{G}}(\tau)
...
...
\frac{d}{dt}{\mathcal{G}}(t+\tau) \right]_{t=-T/2}^{t=T/2} .
\end{displaymath}](img1661.gif) |
(D.3) |
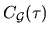 is well-defined if
is well-defined if
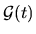 is a stationary process
[79],
i.e. its statistical properties, in particular
its average, do not change with time.
(We have already assumed
is a stationary process
[79],
i.e. its statistical properties, in particular
its average, do not change with time.
(We have already assumed
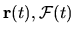 , etc. are stationary
processes).
This condition causes the second term to vanish,
since then
, etc. are stationary
processes).
This condition causes the second term to vanish,
since then
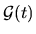 remains bounded.
Integrating the above over all
remains bounded.
Integrating the above over all 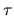 gives an expression for the zeroth
moment: if
gives an expression for the zeroth
moment: if 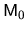 vanishes this
implies
vanishes this
implies
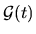 must be stationary.
must be stationary.
Alex Barnett
2001-10-03
![]() we can define
we can define
![]() , whose autocorrelation
function
, whose autocorrelation
function
![]() is related to that of
is related to that of ![]() (using the time-average form (2.30)) by
(using the time-average form (2.30)) by