


Next: Equal wavenumber
Up: Overlaps:
Previous: Overlaps:
The following is an application of Green's theorem.
I start with the vector identity
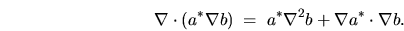 |
(H.3) |
Integrating over 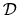 , applying Gauss' Theorem to the LHS and Helmholtz
to the first term on the RHS gives
, applying Gauss' Theorem to the LHS and Helmholtz
to the first term on the RHS gives
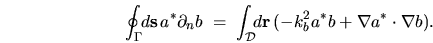 |
(H.4) |
Note that 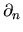 is an abbreviation for
is an abbreviation for
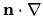 , the local
normal derivative operator at a location
, the local
normal derivative operator at a location 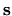 on
on 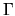 ,
and should not be confused with the cartesian derivatives
,
and should not be confused with the cartesian derivatives
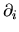 ,
, 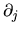 , etc which appear later.
Subtraction of the same equation with the swap
, etc which appear later.
Subtraction of the same equation with the swap
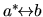 gives the
useful overlap formula
gives the
useful overlap formula
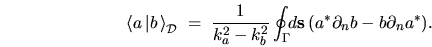 |
(H.5) |
This formula is undefined for 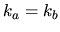 , where the integral vanishes.
Note that if
, where the integral vanishes.
Note that if 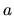 and
and 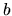 are chosen to obey the same (general mixed) BCs,
the formula gives zero as one would expect for orthogonal eigenstates.
are chosen to obey the same (general mixed) BCs,
the formula gives zero as one would expect for orthogonal eigenstates.
Alex Barnett
2001-10-03