


Next: Matrix trick for pushing
Up: Overlaps:
Previous: Differing wavenumbers
The case 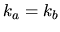 can be reached most easily by setting
can be reached most easily by setting
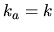 and
and
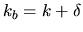 while taking the limit
while taking the limit
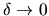 .
The solution
.
The solution 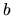 now has to be spatially scaled
(dilated about the arbitrary origin) appropriately for its new wavenumber.
Section 6.1.1 (also Appendix I)
gives the expansion of the dilation operator
at wavenumber
now has to be spatially scaled
(dilated about the arbitrary origin) appropriately for its new wavenumber.
Section 6.1.1 (also Appendix I)
gives the expansion of the dilation operator
at wavenumber 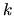 in powers of
in powers of 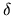 , thus
, thus
![\begin{displaymath}
b(k + \delta;{\mathbf r}) \; = \; \left[ 1 + \frac{\delta}{...
...} \cdot \nabla + O(\delta^2) \cdots \right] b(k;{\mathbf r}) .
\end{displaymath}](img1811.gif) |
(H.6) |
Substitution into (H.5), noting
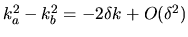 ,
and taking the limit (in which only the lowest
order
,
and taking the limit (in which only the lowest
order 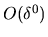 survives) gives
survives) gives
![\begin{displaymath}
\left\langle a \left\vert b\right.\right\rangle _{\mathcal{...
...nabla ({\mathbf r}\cdot\nabla b)
\rule{0in}{0.2in}
\right] .
\end{displaymath}](img1814.gif) |
(H.7) |
This can be shown to be a generalization of the
overlap formula given by Boasman [33] to general 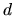 and differing
solutions
and differing
solutions 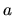 and
and 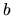 .
Despite the derivation using scaling, (H.7) is in fact
an identity, which can be proved using a messy algebra sequenceH.1.
Unlike the LHS, the RHS is not manifestly
.
Despite the derivation using scaling, (H.7) is in fact
an identity, which can be proved using a messy algebra sequenceH.1.
Unlike the LHS, the RHS is not manifestly
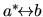 symmetric.
However, it can be written in the symmetrized form (H.14)
derived in the next section.
Notice that the choice
symmetric.
However, it can be written in the symmetrized form (H.14)
derived in the next section.
Notice that the choice 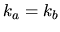 has increased the order of derivative
required on the boundary by one.
has increased the order of derivative
required on the boundary by one.
In the case of Dirichlet BCs the second term in (H.7) vanishes,
and the replacement
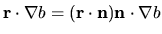 (which follows from the fact that
(which follows from the fact that 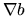 and
and 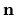 are parallel),
gives
are parallel),
gives
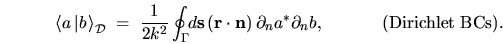 |
(H.8) |
However the knowledge that the LHS is zero for 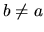 (orthogonal eigenstates)
shows that (H.8) is an exact boundary orthogonality
relation for degenerate Dirichlet eigenstates.
Note that the RHS is proportional to the matrix element
(orthogonal eigenstates)
shows that (H.8) is an exact boundary orthogonality
relation for degenerate Dirichlet eigenstates.
Note that the RHS is proportional to the matrix element
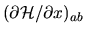 of the billiard dilation deformation between degenerate states
(Appendix C).
On the other hand, choosing
of the billiard dilation deformation between degenerate states
(Appendix C).
On the other hand, choosing 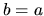 we have
we have
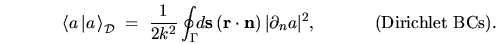 |
(H.9) |
This very useful boundary formula
for the norm of Dirichlet eigenstates
appears to have been found first for 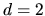 by Berry and
Wilkinson (appendix of [28]). It was since derived in a different
way by Boasman[33], and for general
by Berry and
Wilkinson (appendix of [28]). It was since derived in a different
way by Boasman[33], and for general 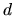 was derived
in our work[14].
However, I believe the new derivation above to be the simplest yet.
was derived
in our work[14].
However, I believe the new derivation above to be the simplest yet.



Next: Matrix trick for pushing
Up: Overlaps:
Previous: Differing wavenumbers
Alex Barnett
2001-10-03
![]() can be reached most easily by setting
can be reached most easily by setting
![]() and
and
![]() while taking the limit
while taking the limit
![]() .
The solution
.
The solution ![]() now has to be spatially scaled
(dilated about the arbitrary origin) appropriately for its new wavenumber.
Section 6.1.1 (also Appendix I)
gives the expansion of the dilation operator
at wavenumber
now has to be spatially scaled
(dilated about the arbitrary origin) appropriately for its new wavenumber.
Section 6.1.1 (also Appendix I)
gives the expansion of the dilation operator
at wavenumber ![]() in powers of
in powers of ![]() , thus
, thus
![]() (which follows from the fact that
(which follows from the fact that ![]() and
and ![]() are parallel),
gives
are parallel),
gives