Next: Other matrix elements
Up: Matrix trick for pushing
Previous: Volume integrals of scalar
A tensor divergence analogy of the above trick can easily be found.
Using Einstein summation convention, one can write tensors on the
LHS whose divergence gives vectors on the RHS,
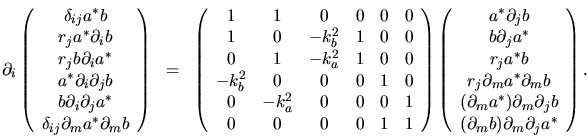 |
(H.15) |
Notice that no dependence on 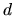 has entered.
The relation can be written
has entered.
The relation can be written
 |
(H.16) |
Remember that Roman indices
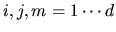 are spatial, whereas Greek indices
are spatial, whereas Greek indices
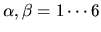 label coefficients.
Note that the vector of vectors
label coefficients.
Note that the vector of vectors
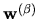 does contain some different functions than
does contain some different functions than
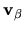 from Section H.2.1.
The matrix determinant is det
from Section H.2.1.
The matrix determinant is det
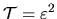 , the same as for
, the same as for 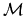 .
The tensor Gauss' theorem is
.
The tensor Gauss' theorem is
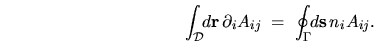 |
(H.17) |
Applying this to the domain integral of
(H.16) gives
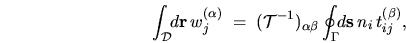 |
(H.18) |
which are the desired closed-form expressions for volume integrals of
(the 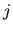 component of) the vector functions
component of) the vector functions
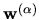 .
The symbolic inverse is found to be,
.
The symbolic inverse is found to be,
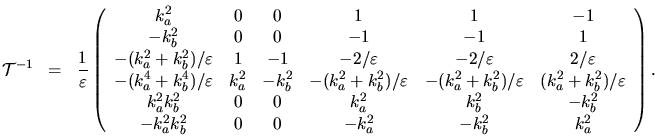 |
(H.19) |
Again, singular solutions can still be found when 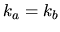 .
The full consequences of these types of matrix relations have not been explored.
.
The full consequences of these types of matrix relations have not been explored.



Next: Other matrix elements
Up: Matrix trick for pushing
Previous: Volume integrals of scalar
Alex Barnett
2001-10-03