


Next: Curvilinear boundary coordinates
Up: Appendix I: Scaling expansion
Previous: Appendix I: Scaling expansion
Expansion of the dilation operator
A scaling wavefunction 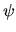 (see Eq.(6.1)) whose
unscaled wavenumber is
(see Eq.(6.1)) whose
unscaled wavenumber is 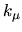 will be rescaled to a new wavenumber
will be rescaled to a new wavenumber
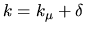 , where
, where 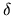 is the wavenumber shift.
Its value at location
is the wavenumber shift.
Its value at location 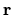 is
is
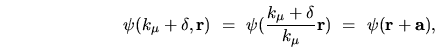 |
(I.1) |
where the translation vector is
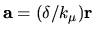 .
Formally this translation can be performed by exponentiation of the
generator of translation [174,7]:
.
Formally this translation can be performed by exponentiation of the
generator of translation [174,7]:
![\begin{displaymath}
\psi(k_\mu + \delta,{\mathbf r}) \ = \ e^{{\mathbf a}\cdot\...
...\cdot\nabla)
({\mathbf a}\cdot\nabla) + \cdots \right] \psi .
\end{displaymath}](img1874.gif) |
(I.2) |
Thus we have written the scaled value in terms of local derivatives of the
unscaled wavefunction.
This becomes a definition of dilation only when the 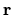 -dependence
of
-dependence
of 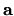 is finally substituted.
Note that
is finally substituted.
Note that 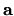 is held constant as far as
is held constant as far as  is concerned.
(This differs from other possible definitions of dilation [14],
where the commutator
is concerned.
(This differs from other possible definitions of dilation [14],
where the commutator
![$[\partial_i,r_j] = \delta_{ij}$](img1876.gif) plays a role;
however my form
will be simpler to expand to high order).
For instance in Cartesian coordinates,
plays a role;
however my form
will be simpler to expand to high order).
For instance in Cartesian coordinates,
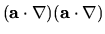 is to be interpreted as
is to be interpreted as
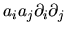 (Einstein summation
assumed), because in Cartesian coordinates
(Einstein summation
assumed), because in Cartesian coordinates
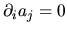 .
.
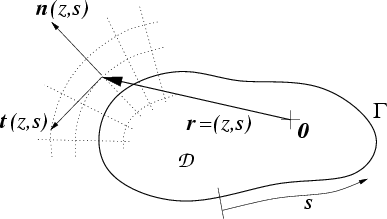
Figure I.1:
Curvilinear coordinates  used to represent points
used to represent points  near the
billiard boundary
near the
billiard boundary  .
The orthogonal unit vectors are the vector fields
.
The orthogonal unit vectors are the vector fields 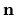 and
and 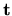 .
.
 |



Next: Curvilinear boundary coordinates
Up: Appendix I: Scaling expansion
Previous: Appendix I: Scaling expansion
Alex Barnett
2001-10-03
![]() (see Eq.(6.1)) whose
unscaled wavenumber is
(see Eq.(6.1)) whose
unscaled wavenumber is ![]() will be rescaled to a new wavenumber
will be rescaled to a new wavenumber
![]() , where
, where ![]() is the wavenumber shift.
Its value at location
is the wavenumber shift.
Its value at location ![]() is
is
