


Next: Tension matrix expansion
Up: Appendix I: Scaling expansion
Previous: Curvilinear boundary coordinates
We now proceed term-by-term in (I.2). The zeroth-order
is
 |
(I.15) |
where the arrow implies application of the Dirichlet boundary conditions (BCs),
namely
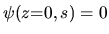 for all
for all  (remember that we already chose
(remember that we already chose  in order to be able to write the metric).
The first order is
in order to be able to write the metric).
The first order is
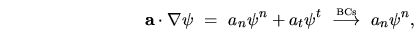 |
(I.16) |
where the result 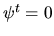 was used. In will use in future the fact that all
higher
was used. In will use in future the fact that all
higher 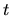 -derivatives
-derivatives
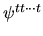 vanish upon application of the BCs.
The second order requires application of the rules (I.10):
vanish upon application of the BCs.
The second order requires application of the rules (I.10):
The Helmholtz equation and the BCs together imply
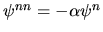 , a relation used both above and below.
In general our task is to reduce the number of
, a relation used both above and below.
In general our task is to reduce the number of 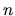 -derivatives; it is always
possible using such manipulations to leave only terms containing a single
-derivatives; it is always
possible using such manipulations to leave only terms containing a single
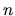 -derivative.
This will be desirable for manipulation of boundary integrals by parts later.
-derivative.
This will be desirable for manipulation of boundary integrals by parts later.
The third-order result (included below) requires use of the following.
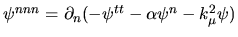 simplifies to
simplifies to
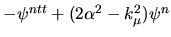 when the BCs are applied.
This required the normal derivative of curvature
when the BCs are applied.
This required the normal derivative of curvature
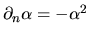 since
since 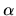 now needs to be regarded as a scalar field with
now needs to be regarded as a scalar field with 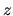 -dependence.
The tangential derivative is given the name
-dependence.
The tangential derivative is given the name
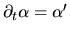 .
Also
.
Also
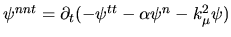 simplifies to
simplifies to
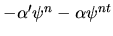 when BCs are applied.
when BCs are applied.
Combining everything and finally substituting for  gives
the expansion of a Dirichlet scaling eigenfunction at location
gives
the expansion of a Dirichlet scaling eigenfunction at location  on
on 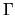 :
:
The expression is believed to be correct to order 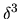 . The
complexity increases greatly with each power of
. The
complexity increases greatly with each power of 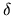 , and higher derivatives
of the curvature
, and higher derivatives
of the curvature 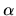 enter.
However, in the case of the circle billiard
(where
enter.
However, in the case of the circle billiard
(where 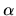 is constant) it is easy to verify the expansion.
One general pattern is that the
is constant) it is easy to verify the expansion.
One general pattern is that the
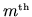 -order terms all contain
-order terms all contain 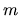 powers
of
powers
of 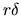 , and for each term the number of spatial derivatives of
, and for each term the number of spatial derivatives of 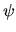 must equal the power of
must equal the power of 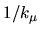 minus the power of
minus the power of 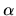 .
It is important to notice
that the
.
It is important to notice
that the 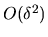 term differs by the presence of a factor of
term differs by the presence of a factor of
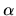 from the
from the 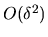 term given by VS.
term given by VS.



Next: Tension matrix expansion
Up: Appendix I: Scaling expansion
Previous: Curvilinear boundary coordinates
Alex Barnett
2001-10-03
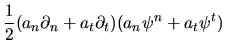
![$\displaystyle \frac{1}{2} \left[ a_n^2 \psi^{nn} + 2 a_n a_t \psi^{nt} + a_t^2 \psi^{tt}
+ \alpha a_t(a_t\psi^n - a_n\psi^t)\right]$](img1927.gif)
![]() simplifies to
simplifies to
![]() when the BCs are applied.
This required the normal derivative of curvature
when the BCs are applied.
This required the normal derivative of curvature
![]() since
since ![]() now needs to be regarded as a scalar field with
now needs to be regarded as a scalar field with ![]() -dependence.
The tangential derivative is given the name
-dependence.
The tangential derivative is given the name
![]() .
Also
.
Also
![]() simplifies to
simplifies to
![]() when BCs are applied.
when BCs are applied.
![]() gives
the expansion of a Dirichlet scaling eigenfunction at location
gives
the expansion of a Dirichlet scaling eigenfunction at location ![]() on
on ![]() :
: