


Next: Useful geometric boundary integrals
Up: Appendix I: Scaling expansion
Previous: Applying boundary conditions and
The tension matrix (using the `dilation' weighting function 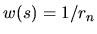 )
in the scaling eigenfunction basis has elements
)
in the scaling eigenfunction basis has elements
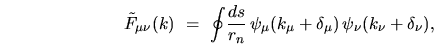 |
(I.19) |
where the wavenumber shifts for the two states involved are
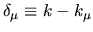 and
and
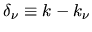 .
As usual I define the wavenumber difference
.
As usual I define the wavenumber difference
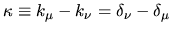 .
Substitution of (I.18) gives a power series in the
.
Substitution of (I.18) gives a power series in the  's,
which we will study and make estimates for
unknown boundary integrals to grasp the general structure.
We will assume for simplicity that the billiard size
's,
which we will study and make estimates for
unknown boundary integrals to grasp the general structure.
We will assume for simplicity that the billiard size
 , and
remain in
, and
remain in  .
We will ignore differences in
.
We will ignore differences in 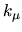 and
and 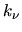 from
from 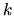 when appropriate,
and look only for the dominant off-diagonal terms.
when appropriate,
and look only for the dominant off-diagonal terms.
The 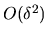 term in
term in 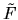 comes
from the lowest order in (I.18),
comes
from the lowest order in (I.18),
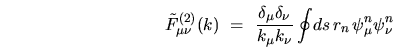 |
(I.20) |
which we can write as
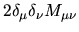 (see Section 6.1.1),
where
(see Section 6.1.1),
where 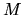 is quasi-diagonal.
The diagonal is
is quasi-diagonal.
The diagonal is
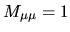 , and
we have from the considerations of Section 6.1.2
small off-diagonal elements of size
, and
we have from the considerations of Section 6.1.2
small off-diagonal elements of size
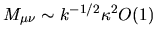 ,
for
,
for  .
.
The  term in
term in 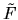 is, after some rearrangement,
is, after some rearrangement,
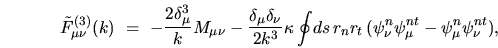 |
(I.21) |
where an integral of
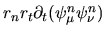 was performed by parts.
This required use of
was performed by parts.
This required use of
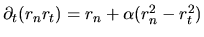 ,
a different expression than found by VS.
It can be proved easily using
,
a different expression than found by VS.
It can be proved easily using
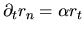 and
and
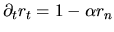 , which follow from (I.8)
and (I.9).
Remarkably, the
, which follow from (I.8)
and (I.9).
Remarkably, the 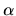 dependence then cancels out, giving the same
dependence then cancels out, giving the same
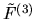 diagonal term as that of VS.
We believe that the integral in (I.21) does not have any
quasi-orthogonal property, so can be estimated using random waves.
The estimate gives
diagonal term as that of VS.
We believe that the integral in (I.21) does not have any
quasi-orthogonal property, so can be estimated using random waves.
The estimate gives 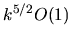 for this integral, and shows that this term
dominates over any off-diagonal contribution from the first term (involving
for this integral, and shows that this term
dominates over any off-diagonal contribution from the first term (involving 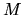 ).
The factor of
).
The factor of 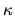 in this term means that there is a weak form
of quasi-diagonality at this order.
Importantly, for
in this term means that there is a weak form
of quasi-diagonality at this order.
Importantly, for 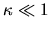 the off-diagonal
the off-diagonal 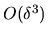 error
renders the
error
renders the 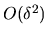 error insignificant.
Hence we expect the quasi-diagonality property of
error insignificant.
Hence we expect the quasi-diagonality property of 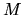 to play no role in errors
in the scaling method.
to play no role in errors
in the scaling method.
The 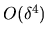 and higher terms in
and higher terms in 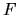 become very messy.
I believe that the
dominant
become very messy.
I believe that the
dominant 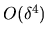 terms, both on and off the diagonal, are
terms, both on and off the diagonal, are
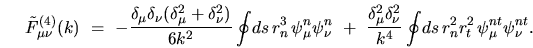 |
(I.22) |
This can be seen by comparing powers of 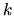 and using random-wave estimates.
A random-wave estimate of the integrals then gives
and using random-wave estimates.
A random-wave estimate of the integrals then gives
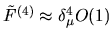 on the diagonal and
on the diagonal and
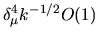 off-diagonal.
Note that the off-diagonal has no quasi-diagonality property at this or higher
orders.
For higher orders
off-diagonal.
Note that the off-diagonal has no quasi-diagonality property at this or higher
orders.
For higher orders 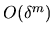 for
for 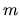 even, we expect
even, we expect
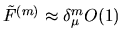 on the diagonal and
on the diagonal and
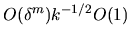 off-diagonal.
For
off-diagonal.
For 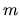 odd, the leading diagonal
terms are down by a factor of
odd, the leading diagonal
terms are down by a factor of 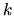 which renders them
insignificant.
which renders them
insignificant.
To summarize, the diagonal of the tension matrix has the form given in
Eq.(6.27), and for
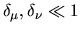 the
dominant off-diagonal terms are
the
dominant off-diagonal terms are
![\begin{displaymath}
\tilde{F}_{\mu\nu}(k) \ \approx \
\frac{\delta_\mu\delta_\...
... O(1) +
\delta_\mu\delta_\nu O(1) \rule{0in}{0.2in} \right] .
\end{displaymath}](img1973.gif) |
(I.23) |
Here contributions from orders 3 and 4 were included because it may be
that the 4th order (the lowest order with no quasi-diagonality,
i.e. no powers of 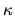 ) contributes most to errors in the scaling method.
It is important to note that the 2nd order term (due to off-diagonal strength
of
) contributes most to errors in the scaling method.
It is important to note that the 2nd order term (due to off-diagonal strength
of 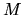 ) is negligible.
It is clear that more research is needed on the properties of the higher-order
terms, especially if an explanation of the tension error
) is negligible.
It is clear that more research is needed on the properties of the higher-order
terms, especially if an explanation of the tension error 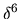 power-law
growth (Section 6.3.1) is sought.
power-law
growth (Section 6.3.1) is sought.



Next: Useful geometric boundary integrals
Up: Appendix I: Scaling expansion
Previous: Applying boundary conditions and
Alex Barnett
2001-10-03
![]() )
in the scaling eigenfunction basis has elements
)
in the scaling eigenfunction basis has elements
![]() term in
term in ![]() comes
from the lowest order in (I.18),
comes
from the lowest order in (I.18),
![]() term in
term in ![]() is, after some rearrangement,
is, after some rearrangement,
![]() and higher terms in
and higher terms in ![]() become very messy.
I believe that the
dominant
become very messy.
I believe that the
dominant ![]() terms, both on and off the diagonal, are
terms, both on and off the diagonal, are
![]() the
dominant off-diagonal terms are
the
dominant off-diagonal terms are