


Next: Real plane waves (RPWs)
Up: Appendix J: Helmholtz basis
Previous: Appendix J: Helmholtz basis
Generally the best (in the least squares sense in the linear Helmholtz
function space)
coefficient vector 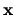 able to represent a true
(domain-normalized) eigenstate
has exponentially large coefficients.
This can be expressed (following Vergini [194])
in terms of a basis `badness',
able to represent a true
(domain-normalized) eigenstate
has exponentially large coefficients.
This can be expressed (following Vergini [194])
in terms of a basis `badness',
 |
(J.2) |
which diverges exponentially once the basis set size 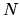 is increased
beyond
is increased
beyond 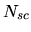 .
Numerically, because of the null-space truncation of Section 5.3.2,
.
Numerically, because of the null-space truncation of Section 5.3.2,
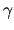 has an upper limit of
has an upper limit of
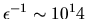 .
This issue is identical to the divergence of basis coefficients found
by Dietz et al. when attempting to expand a `cake billiard' eigenfunction in terms
of plane waves (or angular-momentum states) [63].
The problem is that of representing evanescent components, which are
generally present in billiard eigenfunctions, by distributions
of real plane waves.
As Berry has shown [26], rapidly-oscillating distributions
are required which grow exponentially with the number of
wavelengths across the system and with the evanescence parameter.
This was well understood by Vergini, who demonstrated that
improving the basis by adding a small number of evanescent plane waves
(in the case of the stadium only)
enabled
.
This issue is identical to the divergence of basis coefficients found
by Dietz et al. when attempting to expand a `cake billiard' eigenfunction in terms
of plane waves (or angular-momentum states) [63].
The problem is that of representing evanescent components, which are
generally present in billiard eigenfunctions, by distributions
of real plane waves.
As Berry has shown [26], rapidly-oscillating distributions
are required which grow exponentially with the number of
wavelengths across the system and with the evanescence parameter.
This was well understood by Vergini, who demonstrated that
improving the basis by adding a small number of evanescent plane waves
(in the case of the stadium only)
enabled 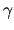 to reach
to reach 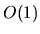 .
This improved the basis tension error
.
This improved the basis tension error
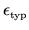 from about
from about 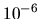 to about
to about 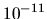 .
.
In general the requirements of a good basis are small
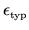 and, if possible,
and, if possible,
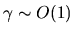 for most states.
I first give the real plane waves,
which work well in many billiard shapes,
then give Vergini's evanescent plane
waves which currently are well-adapted only to the stadium billiard (and shapes
close to it).
for most states.
I first give the real plane waves,
which work well in many billiard shapes,
then give Vergini's evanescent plane
waves which currently are well-adapted only to the stadium billiard (and shapes
close to it).



Next: Real plane waves (RPWs)
Up: Appendix J: Helmholtz basis
Previous: Appendix J: Helmholtz basis
Alex Barnett
2001-10-03
![]() able to represent a true
(domain-normalized) eigenstate
has exponentially large coefficients.
This can be expressed (following Vergini [194])
in terms of a basis `badness',
able to represent a true
(domain-normalized) eigenstate
has exponentially large coefficients.
This can be expressed (following Vergini [194])
in terms of a basis `badness',
![]() and, if possible,
and, if possible,
![]() for most states.
I first give the real plane waves,
which work well in many billiard shapes,
then give Vergini's evanescent plane
waves which currently are well-adapted only to the stadium billiard (and shapes
close to it).
for most states.
I first give the real plane waves,
which work well in many billiard shapes,
then give Vergini's evanescent plane
waves which currently are well-adapted only to the stadium billiard (and shapes
close to it).