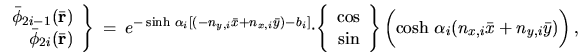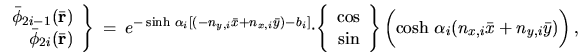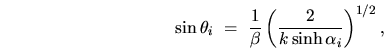Next: Symmetrization and reduction of
Up: Appendix J: Helmholtz basis
Previous: Real plane waves (RPWs)
Evanescent plane waves (EPWs) are given a good introduction in [26].
Vergini [194] developed a set of EPWs for the stadium
which involved `families' with increasing evanescence parameter,
which he arranged to become increasingly localized at the stadium
curvature-discontinuity point P (see Fig. J.1).
I found a single such family to be sufficient.
Following Vergini's recipe, the EPWs are
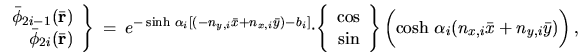 |
(J.5) |
for
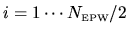 .
For each
.
For each 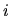 , the propagation direction
, the propagation direction
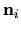 (parallel to the wavevector
(parallel to the wavevector 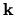 ) points along
) points along
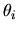 , and the growth and decay directions are perpendicular to this.
The evanescence parameters are given by an algebraic progression,
, and the growth and decay directions are perpendicular to this.
The evanescence parameters are given by an algebraic progression,
 |
(J.6) |
The angles (restricted to the 2nd quadrant ![$[\pi/2,\pi]$](img2001.gif) )
are chosen so as to `balance' the EPW to roughly
equal weight on the boundary either side of the point P:
)
are chosen so as to `balance' the EPW to roughly
equal weight on the boundary either side of the point P:
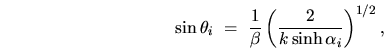 |
(J.7) |
where the balancing is controlled by the constant 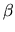 .
I found
.
I found 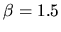 optimal (Vergini reports
optimal (Vergini reports 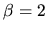 and uses a second
family at
and uses a second
family at 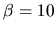 ).
The impact parameters
).
The impact parameters 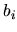 (see Fig. J.1) are such that the
maximum value of
(see Fig. J.1) are such that the
maximum value of 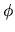 on the boundary is unity.
The number
on the boundary is unity.
The number
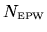 is chosen so that the maximum
is chosen so that the maximum 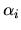 is about 3
(the limit on
is about 3
(the limit on 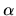 is discussed in Section 6.3.3).
At
is discussed in Section 6.3.3).
At 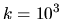 ,
,
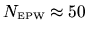 is sufficient.
So even though the EPW functions take longer to evaluate than RPWs
(especially when symmetrized, see below),
there are so few that their computational effort remains small.
is sufficient.
So even though the EPW functions take longer to evaluate than RPWs
(especially when symmetrized, see below),
there are so few that their computational effort remains small.



Next: Symmetrization and reduction of
Up: Appendix J: Helmholtz basis
Previous: Real plane waves (RPWs)
Alex Barnett
2001-10-03