


Next: Microcanonical averages and trajectory
Up: Review of classical dissipation
Previous: Fokker-Planck equation for energy
Irreversible growth of average energy
How does the energy spreading cause growth of the average energy?
It is a result of both the
diffusion term
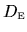 being energy-dependent,
and of the extra drift (bias) due to transformation from
being energy-dependent,
and of the extra drift (bias) due to transformation from 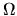 to
to 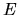 (see Fig. 2.2b).
In the billiard context, the former effect is easy to visualize:
we can imagine that particles which happen to
have a slightly increased kinetic energy will hit the walls more often,
thus diffusing faster in energy.
We will see in Chapter 4 that the
dependence is
(see Fig. 2.2b).
In the billiard context, the former effect is easy to visualize:
we can imagine that particles which happen to
have a slightly increased kinetic energy will hit the walls more often,
thus diffusing faster in energy.
We will see in Chapter 4 that the
dependence is
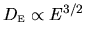 , independent of
, independent of 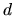 .
The latter effect is less intuitive.
Considering that
.
The latter effect is less intuitive.
Considering that
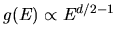 for billiards it is not hard to show that the ratio of the latter to the
former effect is
for billiards it is not hard to show that the ratio of the latter to the
former effect is 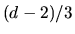 , independent of energy.
Therefore which effect dominates depends on
, independent of energy.
Therefore which effect dominates depends on 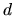 the system dimensionality.
the system dimensionality.
We compute the rate of change of average energy, substituting
(2.21) and integrating by parts,
The first term is the reversible heating (easily verified
using the microcanonical case
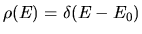 ). The second
is irreversible since it relies on diffusion; it can be written
(by substituting for
). The second
is irreversible since it relies on diffusion; it can be written
(by substituting for
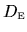 ) as
) as
 |
(2.23) |
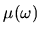 is a friction coefficient, named so because
he agency moving
is a friction coefficient, named so because
he agency moving 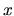 has to do work against a nonzero
average force.
We have ohmic dissipation,
corresponding to an average force
has to do work against a nonzero
average force.
We have ohmic dissipation,
corresponding to an average force
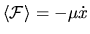 which is proportional to velocity.
The value of
which is proportional to velocity.
The value of 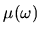 depends on the
energy distribution
depends on the
energy distribution 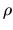 at time
at time 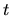 , and has the general expression
, and has the general expression
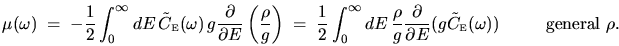 |
(2.24) |
It is interesting that Koonin and Randrup
derived an equivalent expression (Eq. (2.23) of [120]), without
explicitly considering energy spreading.
If we start in a particular choice of ensemble (initial 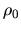 ),
and diffusion has not yet caused
),
and diffusion has not yet caused 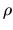 to differ much from
to differ much from 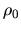 ,
then
,
then 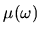 therefore takes special forms:
therefore takes special forms:
where the subscript
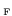 means evaluation at the Fermi energy
means evaluation at the Fermi energy
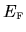 .
The Fermi distribution has a
constant phase-space density of
.
The Fermi distribution has a
constant phase-space density of
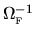 ,
normalised to represent a single particle.
For an application to many non-interacting fermions, see
Section 2.2.4.
The case of the canonical distribution,
relevant to a thermal gas of non-interacting classical particles,
is covered by Cohen (Section 4 of [46]) and I do not discuss it here.
After long times, if the system remains isolated,
it can be that
,
normalised to represent a single particle.
For an application to many non-interacting fermions, see
Section 2.2.4.
The case of the canonical distribution,
relevant to a thermal gas of non-interacting classical particles,
is covered by Cohen (Section 4 of [46]) and I do not discuss it here.
After long times, if the system remains isolated,
it can be that 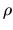 is very different from
is very different from 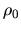 ,
and the special forms (2.25)
or (2.26) will have to be replaced by (2.24).
,
and the special forms (2.25)
or (2.26) will have to be replaced by (2.24).
What I have presented is only the dissipation
appearing to lowest order in 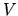 (Jarzynski [107] discusses this by way
of an expansion in powers of a `slowness parameter'
(Jarzynski [107] discusses this by way
of an expansion in powers of a `slowness parameter' 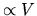 ).
There will be higher-order terms in the friction which
become more relevant as
).
There will be higher-order terms in the friction which
become more relevant as 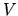 approaches
for example the limit (2.12).
There are other ways that the classical spreading picture can break down.
For instance for
approaches
for example the limit (2.12).
There are other ways that the classical spreading picture can break down.
For instance for 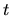 less than the correlation time
less than the correlation time
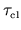 the energy spreading
should be much less than
the energy spreading
should be much less than 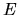 itself.
Also for this same
itself.
Also for this same 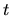 the
average energy increase should remain small compared to the spreading.
These set additional upper limits on
the
average energy increase should remain small compared to the spreading.
These set additional upper limits on 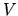 [46].
[46].



Next: Microcanonical averages and trajectory
Up: Review of classical dissipation
Previous: Fokker-Planck equation for energy
Alex Barnett
2001-10-03
![]() being energy-dependent,
and of the extra drift (bias) due to transformation from
being energy-dependent,
and of the extra drift (bias) due to transformation from ![]() to
to ![]() (see Fig. 2.2b).
In the billiard context, the former effect is easy to visualize:
we can imagine that particles which happen to
have a slightly increased kinetic energy will hit the walls more often,
thus diffusing faster in energy.
We will see in Chapter 4 that the
dependence is
(see Fig. 2.2b).
In the billiard context, the former effect is easy to visualize:
we can imagine that particles which happen to
have a slightly increased kinetic energy will hit the walls more often,
thus diffusing faster in energy.
We will see in Chapter 4 that the
dependence is
![]() , independent of
, independent of ![]() .
The latter effect is less intuitive.
Considering that
.
The latter effect is less intuitive.
Considering that
![]() for billiards it is not hard to show that the ratio of the latter to the
former effect is
for billiards it is not hard to show that the ratio of the latter to the
former effect is ![]() , independent of energy.
Therefore which effect dominates depends on
, independent of energy.
Therefore which effect dominates depends on ![]() the system dimensionality.
the system dimensionality.
![]() (Jarzynski [107] discusses this by way
of an expansion in powers of a `slowness parameter'
(Jarzynski [107] discusses this by way
of an expansion in powers of a `slowness parameter' ![]() ).
There will be higher-order terms in the friction which
become more relevant as
).
There will be higher-order terms in the friction which
become more relevant as ![]() approaches
for example the limit (2.12).
There are other ways that the classical spreading picture can break down.
For instance for
approaches
for example the limit (2.12).
There are other ways that the classical spreading picture can break down.
For instance for ![]() less than the correlation time
less than the correlation time
![]() the energy spreading
should be much less than
the energy spreading
should be much less than ![]() itself.
Also for this same
itself.
Also for this same ![]() the
average energy increase should remain small compared to the spreading.
These set additional upper limits on
the
average energy increase should remain small compared to the spreading.
These set additional upper limits on ![]() [46].
[46].