


Next: Review of the linear
Up: Review of classical dissipation
Previous: Irreversible growth of average
Microcanonical averages and trajectory averages
In the preceding sections 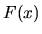 and
and
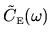 were defined in terms of
the microcanonical average over initial conditions,
were defined in terms of
the microcanonical average over initial conditions,
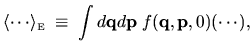 |
|
|
(2.27) |
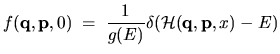 |
|
|
(2.28) |
The assumption
was made that the change in 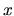 over the correlation time
over the correlation time
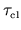 is
insignificant.
This means that the `frozen' Hamiltonian (at fixed
is
insignificant.
This means that the `frozen' Hamiltonian (at fixed 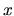 ) can
be used, so the distribution is unchanging in time
) can
be used, so the distribution is unchanging in time
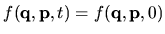 .
All resulting averages are constant in time
(or, if they involve multiple times, they are functions of time differences
only),
and the choice of initial
time
.
All resulting averages are constant in time
(or, if they involve multiple times, they are functions of time differences
only),
and the choice of initial
time 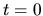 is arbitrary.
is arbitrary.
However, these averages need not be taken using an average over phase space.
By ergodicity [79], they are equal to time averages over a single
trajectory.
Namely, the conservative force (2.3) can be written
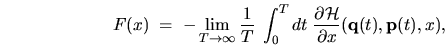 |
(2.29) |
seen to be the mean force due to motion of a
single particle in the system.
Similarly, the auto-correlation is written
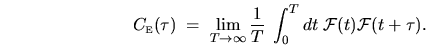 |
(2.30) |
There is now an issue of convergence: the number of independent
samples of any quantity along a trajectory is
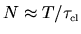 , and
the fractional error of the estimate of the above quantities converges
slowly as
, and
the fractional error of the estimate of the above quantities converges
slowly as 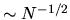 .
Therefore very long trajectories are required to get good estimates.
However, this is often easier than performing the
.
Therefore very long trajectories are required to get good estimates.
However, this is often easier than performing the 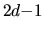 dimensional integral
over the energy shell which would be required for the explicit
evaluation of the phase-space average,
especially since the integrand in (2.30) already involves
propagation forward
in time.
This technique of evaluation of a multi-dimensional integral using a random
sample of points taken from the distribution function is called
Monte Carlo integration [161].
However, in practice, rather than compute
dimensional integral
over the energy shell which would be required for the explicit
evaluation of the phase-space average,
especially since the integrand in (2.30) already involves
propagation forward
in time.
This technique of evaluation of a multi-dimensional integral using a random
sample of points taken from the distribution function is called
Monte Carlo integration [161].
However, in practice, rather than compute
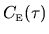 and take the
Fourier transform,
and take the
Fourier transform,
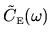 is most efficiently
estimated directly from the Fourier transform of
is most efficiently
estimated directly from the Fourier transform of
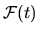 . This approach is discussed
in detail in Appendix B.
. This approach is discussed
in detail in Appendix B.
In an identical fashion to that shown in Fig. 2.2a,
Eq.(2.30) describes
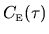 as the projection
of the function
as the projection
of the function
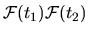 onto the
onto the
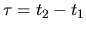 axis.
However only a single trajectory is involved, so
axis.
However only a single trajectory is involved, so
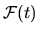 is noisy, and
an average over the time axis
is noisy, and
an average over the time axis
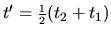 is required.
In this figure, one can imagine the `box'
of allowed
is required.
In this figure, one can imagine the `box'
of allowed 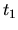 ,
,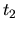 values now bounded by
values now bounded by ![$[0,T]$](img231.gif) .
The average converges in the limit
.
The average converges in the limit
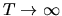 .
.
An instructive convergence
issue arises if we extend this single-trajectory estimate
to the noise intensity
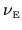 . Naive use of (2.14) and (2.30) would give
. Naive use of (2.14) and (2.30) would give
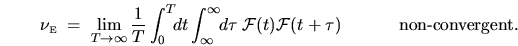 |
(2.31) |
This does not converge because the  integral involves an infinite number
of similarly-sized contributions (the integrand is similar in size for
all
integral involves an infinite number
of similarly-sized contributions (the integrand is similar in size for
all 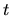 ,
, 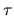 ). Averaging over any finite
). Averaging over any finite 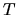 cannot remove this divergence.
Another option is to look back to Eq.(2.8) which is responsible
for the appearance of
cannot remove this divergence.
Another option is to look back to Eq.(2.8) which is responsible
for the appearance of
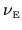 in the spreading rate.
So I could define
in the spreading rate.
So I could define
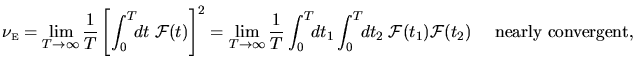 |
(2.32) |
which is the same integral (2.31) with different limits.
This is simply proportional to the energy variance 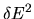 after time
after time 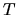 for the single trajectory involved, divided by
for the single trajectory involved, divided by 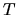 .
The term inside the square brackets is simply a random walk (on timescales
.
The term inside the square brackets is simply a random walk (on timescales
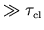 ), giving a Gaussian distribution whose variance grows linearly.
Therefore this estimate of
), giving a Gaussian distribution whose variance grows linearly.
Therefore this estimate of
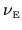 will not converge, rather it will wander
for all
will not converge, rather it will wander
for all
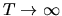 , taking values with a
, taking values with a 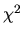 distribution
whose mean is the correct
distribution
whose mean is the correct
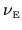 . In effect this reproduces exactly the
stochastic energy spreading whose variance is desired!
However, it is `more convergent' than (2.31).
A convergent estimate can only be created by limiting the
. In effect this reproduces exactly the
stochastic energy spreading whose variance is desired!
However, it is `more convergent' than (2.31).
A convergent estimate can only be created by limiting the 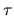 integration
further, to give
integration
further, to give
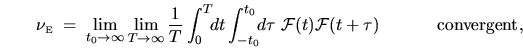 |
(2.33) |
which will converge once
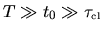 .
In essence the convergence arises because the limits do not allow the
number of independent
.
In essence the convergence arises because the limits do not allow the
number of independent
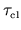 -squared-sized `patches' of the integrand to
grow as fast as
-squared-sized `patches' of the integrand to
grow as fast as 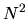 , where
, where 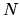 is defined as above.
The nearly-convergent case (2.32) corresponds to
exactly
is defined as above.
The nearly-convergent case (2.32) corresponds to
exactly 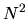 growth.
growth.
The above considerations will not relate directly to the numerical method
of finding
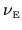 (which will be via
(which will be via
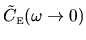 ).
However they serve to warn and provide intuition about convergence
when a single trajectory is used for estimation.
).
However they serve to warn and provide intuition about convergence
when a single trajectory is used for estimation.



Next: Review of the linear
Up: Review of classical dissipation
Previous: Irreversible growth of average
Alex Barnett
2001-10-03
![]() and
and
![]() were defined in terms of
the microcanonical average over initial conditions,
were defined in terms of
the microcanonical average over initial conditions,
![]() as the projection
of the function
as the projection
of the function
![]() onto the
onto the
![]() axis.
However only a single trajectory is involved, so
axis.
However only a single trajectory is involved, so
![]() is noisy, and
an average over the time axis
is noisy, and
an average over the time axis
![]() is required.
In this figure, one can imagine the `box'
of allowed
is required.
In this figure, one can imagine the `box'
of allowed ![]() ,
,![]() values now bounded by
values now bounded by ![]() .
The average converges in the limit
.
The average converges in the limit
![]() .
.
![]() . Naive use of (2.14) and (2.30) would give
. Naive use of (2.14) and (2.30) would give
![]() (which will be via
(which will be via
![]() ).
However they serve to warn and provide intuition about convergence
when a single trajectory is used for estimation.
).
However they serve to warn and provide intuition about convergence
when a single trajectory is used for estimation.