


Next: Addition of deformations: numerical
Up: Chapter 4: Improving upon
Previous: Chapter 4: Improving upon
Decomposition of general deformations
The failure of the WNA for `special' deformations also
extends to the much wider class of deformations which are similar
to special. This is demonstrated in Fig. 4.1.
It should be emphasized that this failure
happens even if the cavity is strongly chaotic.
We seek an analytical estimate for
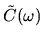 ,
and in particular for its zero-frequency limit
,
and in particular for its zero-frequency limit  .
This estimate should apply to any (general) deformation,
including the case of `close-to-special' deformations.
It would be useful to regard any general deformation
as a combination of `special' component and `normal' component.
The formulation of this idea is the
theme of the present section. Supporting numerical
evidence is gathered in the next section.
.
This estimate should apply to any (general) deformation,
including the case of `close-to-special' deformations.
It would be useful to regard any general deformation
as a combination of `special' component and `normal' component.
The formulation of this idea is the
theme of the present section. Supporting numerical
evidence is gathered in the next section.
The special deformations (for which we have  )
constitute a linear space, meaning that any sum
of special deformations is also a special one.
Now we would like to conjecture that there is also
a linear space of `normal' deformations. By definition,
for `normal' deformation
)
constitute a linear space, meaning that any sum
of special deformations is also a special one.
Now we would like to conjecture that there is also
a linear space of `normal' deformations. By definition,
for `normal' deformation
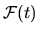 looks like
an uncorrelated random sequence of impulses, and
consequently the WNA is a reasonable approximation.
The notion of randomness can be better formulated
as in Appendix F leading to Eq.(F.4).
However in practice (F.4) is not useful, because
it cannot be applied as an actual classification tool.
(Eq.(F.4) is never satisfied exactly).
Still we are going to demonstrate that there is a
unique way to identify the subspace of normal deformations,
if we insist on a maximal (i.e. the most inclusive)
definition of this subspace.
looks like
an uncorrelated random sequence of impulses, and
consequently the WNA is a reasonable approximation.
The notion of randomness can be better formulated
as in Appendix F leading to Eq.(F.4).
However in practice (F.4) is not useful, because
it cannot be applied as an actual classification tool.
(Eq.(F.4) is never satisfied exactly).
Still we are going to demonstrate that there is a
unique way to identify the subspace of normal deformations,
if we insist on a maximal (i.e. the most inclusive)
definition of this subspace.
It is important to clarify the heuristic reasoning for
having a linear space of normal deformations.
The
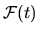 that corresponds to some normal
deformation
that corresponds to some normal
deformation
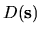 looks like white noise.
It means that only self-correlations of its spikes
are statistically significant. If we have
two such generic quantities,
say
looks like white noise.
It means that only self-correlations of its spikes
are statistically significant. If we have
two such generic quantities,
say
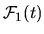 and
and
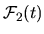 ,
then we expect
,
then we expect
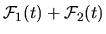 to share the same property.
to share the same property.
The correlation function
of
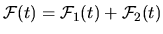 can be written formally as
can be written formally as
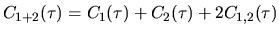 |
|
|
(4.2) |
where 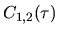 is the cross-correlation function.
In Appendix E we argue the following
is the cross-correlation function.
In Appendix E we argue the following
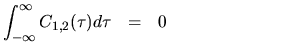 |
|
|
|
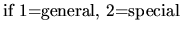 |
|
|
(4.3) |
This can also be proved easily using the fact that
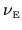 is an exact
quadratic form (3.5) in the function space of
is an exact
quadratic form (3.5) in the function space of
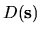 .
(Consider that the special deformations are eigenvectors of this quadratic form
with zero eigenvalue, i.e. they lie in the null-space [188]).
The result is exact, and does not involve any approximation.
In Appendix F we argue the following
.
(Consider that the special deformations are eigenvectors of this quadratic form
with zero eigenvalue, i.e. they lie in the null-space [188]).
The result is exact, and does not involve any approximation.
In Appendix F we argue the following
![$\displaystyle C_{1,2}(\tau) \; \approx \; c \times
\left[
\oint \! D_1({\mathbf s})D_2({\mathbf s}) d{\mathbf s}
\right]
\delta(\tau)
\hspace*{0.5cm}$](img593.gif) |
|
|
|
 |
|
|
(4.4) |
where
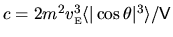 .
This result is an approximation, which is expected
to be as good as our assumption regarding the
`normality' of the deformation
.
This result is an approximation, which is expected
to be as good as our assumption regarding the
`normality' of the deformation
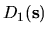 .
Consider now the case where
.
Consider now the case where
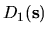 is normal
and
is normal
and
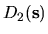 is special. Both Eq.(4.3)
and Eq.(4.4) should apply. But these equations
are consistent if and only if
is special. Both Eq.(4.3)
and Eq.(4.4) should apply. But these equations
are consistent if and only if
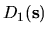 is
orthogonal to
is
orthogonal to
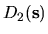 .
We say that
.
We say that
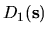 and
and
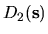 are orthogonal (
are orthogonal (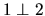 ) using the
following definition:
) using the
following definition:
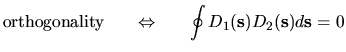 |
|
|
(4.5) |
Thus we have proved that normal deformations must be
orthogonal (in the sense of (4.5)) to special
deformations. Obviously we have proved here a necessary
rather than a sufficient condition for `normality'.
However, if we insist on a maximal definition for the
subspace of normal deformations, then we get a unique
identification. Namely, a deformation is classified
as `normal' if it is orthogonal to the subspace of
special deformations.
The practical consequences of Eq.(4.3)
and Eq.(4.4) are as follows:
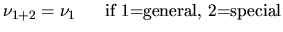 |
|
|
(4.6) |
and
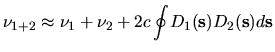 |
|
|
|
 |
|
|
(4.7) |
These results are tested in the next section.
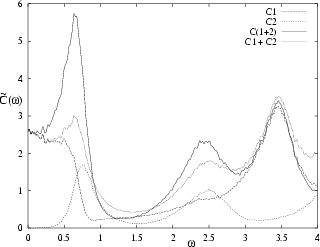
Figure 4.2:
Addition of two `good' normal deformations (1=P2, 2=WG).
The two are orthogonal in the sense of (4.5).
That they are `good' can be seen by their good agreement with their WNA
results (horizontal arrows).
The power spectrum of the sum agrees well with the sum of the power
spectra.
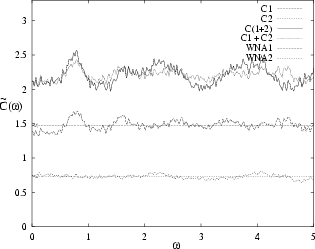 |
Figure 4.3:
Addition of two `bad' normal deformations (1=FR, 2=SX).
The two are orthogonal in the sense of (4.5).
That they are `bad' is shown by a lack of agreement with their WNAs.
The power spectrum of the sum is badly approximated
by the sum of the power spectra (non-linear addition).
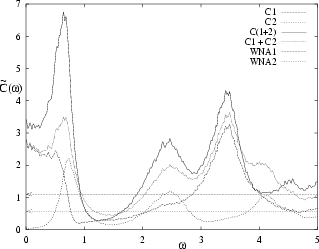 |
Figure 4.4:
Addition of a `good' normal deformation (1=WG)
to a general deformation (2=SX).
The two are orthogonal in the sense of (4.5).
The power spectrum of the sum agrees well with
the sum of the power spectra.
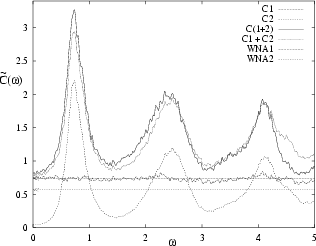 |
Figure 4.5:
Addition of a general deformation (1=FR)
to a `special' deformation (2=TX).
The power spectrum of the sum coincides with the
sum of the power spectra in the limit
 ,
as implied by Eq.(4.6).
,
as implied by Eq.(4.6).
 |



Next: Addition of deformations: numerical
Up: Chapter 4: Improving upon
Previous: Chapter 4: Improving upon
Alex Barnett
2001-10-03
![]() ,
and in particular for its zero-frequency limit
,
and in particular for its zero-frequency limit ![]() .
This estimate should apply to any (general) deformation,
including the case of `close-to-special' deformations.
It would be useful to regard any general deformation
as a combination of `special' component and `normal' component.
The formulation of this idea is the
theme of the present section. Supporting numerical
evidence is gathered in the next section.
.
This estimate should apply to any (general) deformation,
including the case of `close-to-special' deformations.
It would be useful to regard any general deformation
as a combination of `special' component and `normal' component.
The formulation of this idea is the
theme of the present section. Supporting numerical
evidence is gathered in the next section.
![]() )
constitute a linear space, meaning that any sum
of special deformations is also a special one.
Now we would like to conjecture that there is also
a linear space of `normal' deformations. By definition,
for `normal' deformation
)
constitute a linear space, meaning that any sum
of special deformations is also a special one.
Now we would like to conjecture that there is also
a linear space of `normal' deformations. By definition,
for `normal' deformation
![]() looks like
an uncorrelated random sequence of impulses, and
consequently the WNA is a reasonable approximation.
The notion of randomness can be better formulated
as in Appendix F leading to Eq.(F.4).
However in practice (F.4) is not useful, because
it cannot be applied as an actual classification tool.
(Eq.(F.4) is never satisfied exactly).
Still we are going to demonstrate that there is a
unique way to identify the subspace of normal deformations,
if we insist on a maximal (i.e. the most inclusive)
definition of this subspace.
looks like
an uncorrelated random sequence of impulses, and
consequently the WNA is a reasonable approximation.
The notion of randomness can be better formulated
as in Appendix F leading to Eq.(F.4).
However in practice (F.4) is not useful, because
it cannot be applied as an actual classification tool.
(Eq.(F.4) is never satisfied exactly).
Still we are going to demonstrate that there is a
unique way to identify the subspace of normal deformations,
if we insist on a maximal (i.e. the most inclusive)
definition of this subspace.
![]() that corresponds to some normal
deformation
that corresponds to some normal
deformation
![]() looks like white noise.
It means that only self-correlations of its spikes
are statistically significant. If we have
two such generic quantities,
say
looks like white noise.
It means that only self-correlations of its spikes
are statistically significant. If we have
two such generic quantities,
say
![]() and
and
![]() ,
then we expect
,
then we expect
![]() to share the same property.
to share the same property.
![]() can be written formally as
can be written formally as



