Next: Introduction and history of
Up: Dissipation in Deforming Chaotic
Previous: Historical remarks and conclusion
Chapter 5: Improved sweep methods for billiard quantization
In this chapter I describe a numerical method for finding billiard eigenstates
which involves `sweeping' the energy to locate the states.
It is a generalization of and improvement upon
Heller's Plane Wave Decomposition Method (PWDM)
[90,91].
The PWDM was invented over 15 years ago and provided a
more powerful and rapid way to find eigenstates in certain billiard shapes
than had been available beforehand.
In this chapter
several problems of the PWDM have been solved (missing states,
sensitivity to choice of basis set size and number of matching points),
it has been simplified, the accuracy is improved, and the
speed has been increased considerably.
This chapter is also a useful introduction to the following one,
where a much more efficient method (which bypasses the `sweep' altogether)
is analysed.
Subsections
Alex Barnett
2001-10-03
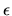 for truncation
for truncation