


Next: Exact form on the
Up: The choice of norm
Previous: The choice of norm
The simplest approximation to 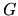 involves approximating the domain integral
by a sum over
involves approximating the domain integral
by a sum over 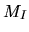 interior points:
interior points:
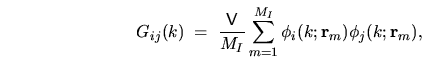 |
(5.18) |
where 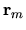 are points inside
are points inside 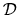 .
In the case of a uniform grid spacing
.
In the case of a uniform grid spacing 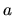 for these points, convergence
would be reached for
for these points, convergence
would be reached for 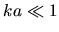 (and resulting error converges like
(and resulting error converges like
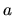 , in numerical experiments), requiring a very large
number
, in numerical experiments), requiring a very large
number
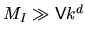 .
In this case all the advantages of a boundary method are lost.
However, a Monte Carlo estimate can be reached for a much smaller
.
In this case all the advantages of a boundary method are lost.
However, a Monte Carlo estimate can be reached for a much smaller 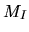 :
in general the estimation error will be Gaussian with a width
:
in general the estimation error will be Gaussian with a width
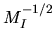 as a fraction of the value.
This requires that the points be chosen in `statistically independent'
regions of the wavefunction, a criterion which for ergodic systems
(excluding heavily-scarred states) it is easy to fulfill.
The slow convergence means that accuracy cannot be high.
Generally an optimal choice for
as a fraction of the value.
This requires that the points be chosen in `statistically independent'
regions of the wavefunction, a criterion which for ergodic systems
(excluding heavily-scarred states) it is easy to fulfill.
The slow convergence means that accuracy cannot be high.
Generally an optimal choice for 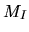 is such that the time spent evaluating
is such that the time spent evaluating
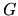 is no more than for
is no more than for 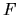 , preserving the `boundary' scaling of the method.
This method has the
advantage of simplicity: only basis function values are required
(the exact form below requires values and derivatives).
, preserving the `boundary' scaling of the method.
This method has the
advantage of simplicity: only basis function values are required
(the exact form below requires values and derivatives).
The case 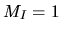 is interesting, since it corresponds to the original
recipe of
Heller [91]. This recipe involves finding the closest
solution to
is interesting, since it corresponds to the original
recipe of
Heller [91]. This recipe involves finding the closest
solution to
 |
(5.19) |
where
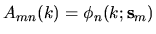 , and
, and
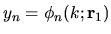 at
the randomly-chosen interior point
at
the randomly-chosen interior point 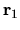 .
Heller's choice of the
.
Heller's choice of the 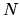 , the number of columns of
, the number of columns of 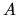 , was about 1.4
times
, was about 1.4
times 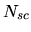 .
The density of boundary matching points
.
The density of boundary matching points 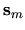 was about 2.6 per wavelength.
It is easy to see that taking the 2-norm of the above equations
gives (5.12) for the version of
was about 2.6 per wavelength.
It is easy to see that taking the 2-norm of the above equations
gives (5.12) for the version of 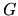 involving a single interior point.
The result
involving a single interior point.
The result
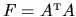 is needed (shown in Appendix G).
The singular value decomposition of
is needed (shown in Appendix G).
The singular value decomposition of 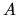 is therefore
equivalent to diagonalization of
is therefore
equivalent to diagonalization of 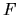 [81].
Looking at Fig. 5.5 one can see that the effect of some of the
eigenstate dips is almost gone, depending on the choice of
[81].
Looking at Fig. 5.5 one can see that the effect of some of the
eigenstate dips is almost gone, depending on the choice of 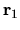 .
Also notice that the transition from one state to another is not very `clean'.
Even though Heller's prescription was then followed by another
normalization
step and a hunt for the resulting normalized tension minima,
if an eigenstate never appears in the solution of the above for any
.
Also notice that the transition from one state to another is not very `clean'.
Even though Heller's prescription was then followed by another
normalization
step and a hunt for the resulting normalized tension minima,
if an eigenstate never appears in the solution of the above for any 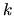 ,
then this normalization step cannot recover it--it becomes a
`missing state'.
,
then this normalization step cannot recover it--it becomes a
`missing state'.
What is the expected fraction of such missing states in Heller's method?
An exact answer is hard, but empirically seems to be of the order of 1%
for the 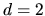 stadium billiard at
stadium billiard at 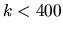 .
(Some users have reported as high as 8% in other systems [136]).
If a true normalized billiard
eigenstate has a very small value of
.
(Some users have reported as high as 8% in other systems [136]).
If a true normalized billiard
eigenstate has a very small value of
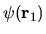 , being
, being
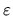 times the RMS value,
then this state's parabolic tension-minimum curve will be multiplied
by
times the RMS value,
then this state's parabolic tension-minimum curve will be multiplied
by 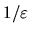 (this multiplication is visible in Fig. 5.5).
If the `dynamic range'
(this multiplication is visible in Fig. 5.5).
If the `dynamic range' 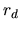 (see Section 5.5.3)
is less than
(see Section 5.5.3)
is less than 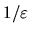 , then the parabola will typically be
`blown' to large enough values that it is obscured by
those of neighboring states, and will never be noticed.
Since the chances of
, then the parabola will typically be
`blown' to large enough values that it is obscured by
those of neighboring states, and will never be noticed.
Since the chances of
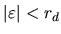 occurring are proportional to
occurring are proportional to 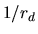 (the Porter-Thomas
probability distribution on
(the Porter-Thomas
probability distribution on
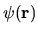 is flat around
is flat around 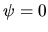 ),
one would expect roughly
),
one would expect roughly 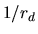 states to be missed.
The dynamic range decreases with increasing
states to be missed.
The dynamic range decreases with increasing 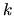 so it is expected that this will become
more severe a problem at high
so it is expected that this will become
more severe a problem at high 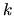 .
.



Next: Exact form on the
Up: The choice of norm
Previous: The choice of norm
Alex Barnett
2001-10-03
![]() involves approximating the domain integral
by a sum over
involves approximating the domain integral
by a sum over ![]() interior points:
interior points:
![]() is interesting, since it corresponds to the original
recipe of
Heller [91]. This recipe involves finding the closest
solution to
is interesting, since it corresponds to the original
recipe of
Heller [91]. This recipe involves finding the closest
solution to
![]() stadium billiard at
stadium billiard at ![]() .
(Some users have reported as high as 8% in other systems [136]).
If a true normalized billiard
eigenstate has a very small value of
.
(Some users have reported as high as 8% in other systems [136]).
If a true normalized billiard
eigenstate has a very small value of
![]() , being
, being
![]() times the RMS value,
then this state's parabolic tension-minimum curve will be multiplied
by
times the RMS value,
then this state's parabolic tension-minimum curve will be multiplied
by ![]() (this multiplication is visible in Fig. 5.5).
If the `dynamic range'
(this multiplication is visible in Fig. 5.5).
If the `dynamic range' ![]() (see Section 5.5.3)
is less than
(see Section 5.5.3)
is less than ![]() , then the parabola will typically be
`blown' to large enough values that it is obscured by
those of neighboring states, and will never be noticed.
Since the chances of
, then the parabola will typically be
`blown' to large enough values that it is obscured by
those of neighboring states, and will never be noticed.
Since the chances of
![]() occurring are proportional to
occurring are proportional to ![]() (the Porter-Thomas
probability distribution on
(the Porter-Thomas
probability distribution on
![]() is flat around
is flat around ![]() ),
one would expect roughly
),
one would expect roughly ![]() states to be missed.
The dynamic range decreases with increasing
states to be missed.
The dynamic range decreases with increasing ![]() so it is expected that this will become
more severe a problem at high
so it is expected that this will become
more severe a problem at high ![]() .
.