


Next: The basic scaling method
Up: Dissipation in Deforming Chaotic
Previous: Conclusion and discussion
Chapter 6: The scaling method of Vergini and Saraceno
Here I explain and analyse the powerful scaling method recently invented
by Vergini and Saraceno (VS) [195,194].
It allows a much more rapid solution of the Helmholtz eigenvalue problem
(5.5) in a hard-walled billiard (with Dirichlet
boundary conditions) than the sweep methods of the previous chapter,
or indeed than any other known method.
The success of the method is essentially due to a single key relation,
namely that eigenstates are quasi-orthogonal
on the boundary (or equivalently, a certain tension matrix is
quasi-diagonal near the diagonal in a basis of rescaled eigenstates).
However, an adequate explanation for the quasi-orthogonality has been sorely
lacking.
The knowledge gained about the band profile of special deformations in
Chapter 3
will provide, for the first time, an understanding of quasi-orthogonality.
This improves upon an (incorrect) guess made by VS, and allows an accurate
semiclassical estimate to be made of the deviation from exact orthogonality.
I give a complete, presentation of the scaling method
(Section 6.1), discuss the utility of higher-order
corrections to the basic method (Section 6.2),
and analyse the various sources of error (Section 6.3).
Conclusions and open issues are brought up in Section 6.5.
Appendix I shows how to evaluate higher-order terms in the
tension matrix, correcting an oversight (to do with boundary curvature)
in the original formulation of VS.
Generally for illustration I will use results for the 2D stadium billiard,
the same shape studied by VS.
This is simply for the reason that excellent evanescent basis sets are known
for this shape, allowing the errors of the method to be distinguished from
those of the basis set.
In the last section I will demonstrate an application to computing the
eigenstates of a stadium deformed by various finite amounts.
The overlaps of these states with the undeformed
states will be studied.
These calculations were published in our work [48].
Note that it is probably useful to have read the previous
chapter to fully appreciate this one.
Subsections



Next: The basic scaling method
Up: Dissipation in Deforming Chaotic
Previous: Conclusion and discussion
Alex Barnett
2001-10-03
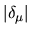
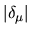 vanishes
vanishes