We have a very-nearly-diagonal form for the tension matrix
for wavenumbers which are close to ![]() , in a scaling eigenfunction basis
(Section 6.1.2).
We consider this matrix and its
derivative with respect to
, in a scaling eigenfunction basis
(Section 6.1.2).
We consider this matrix and its
derivative with respect to ![]() ,
,
The transformation between matrix representations is
| (6.21) | |||
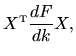 |
(6.22) |
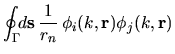 |
(6.23) | ||
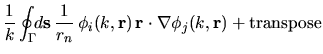 |
(6.24) |
Then diagonalization of the matrix ![]() can give eigenvectors which are very
close to the desired rows of
can give eigenvectors which are very
close to the desired rows of ![]() . In particular, an eigenvector very close to
the scaling eigenfunction
. In particular, an eigenvector very close to
the scaling eigenfunction
![]() may be returned (if
may be returned (if
![]() ). However the eigenvalue will equal the tension of the state resulting
from a unit norm
). However the eigenvalue will equal the tension of the state resulting
from a unit norm
![]() in coefficient space, which has no physical
significance in the basis sets used (RPWs + EPWs). Also the null-space vectors in
in coefficient space, which has no physical
significance in the basis sets used (RPWs + EPWs). Also the null-space vectors in ![]() produce small-eigenvalue
solutions (exponentially spread down to machine precision, as in
Fig. 5.3) which interfere (mix) with the desired vectors.
However the parabolic tension minima are still visible.
The same is true if the matrix
produce small-eigenvalue
solutions (exponentially spread down to machine precision, as in
Fig. 5.3) which interfere (mix) with the desired vectors.
However the parabolic tension minima are still visible.
The same is true if the matrix ![]() is diagonalized, only now small
eigenvalues correspond to both Dirichlet (upwards-travelling) and Neumann
(downwards-travelling) eigenstates.
Therefore direct diagonalization is not a good way to extract the desired
states.
Fig. 6.4 shows the
is diagonalized, only now small
eigenvalues correspond to both Dirichlet (upwards-travelling) and Neumann
(downwards-travelling) eigenstates.
Therefore direct diagonalization is not a good way to extract the desired
states.
Fig. 6.4 shows the ![]() -dependence of these two diagonalizations.
-dependence of these two diagonalizations.