Deformations and eigenstate computation

Examples of a `special' deformation and a `generic' deformation were used (see Chapters 3 and 4). The special deformation chosen was rotation about the origin (lower-left corner). This corresponds to $D(s) = {\mathbf n}(s) \cdot {\mathbf e}_z \times {\mathbf r}(s)$ (see Table 3.2). Because the special deformations preserve shape, the eigenstates of a thus-deformed billiard are unchanged (space is invariant under translation and rotation). Therefore only one set of eigenstates is required for all $x$ values.

The generic deformation used was $D(s) = \sin^2(\theta)$, where $\theta$ is the angle on the circular part of the boundary measured from the vertical. $D(s) = 0$ on the top, left, and bottom straight sections of the boundary. This has the effect of pushing out the curved part into an ellipse (and a corresponding lengthening of the bottom straight section). This deformation was chosen because it was possible to create large deformations with minimum sacrifice to the quality of the basis-dependent tension minima $\epsilon_\mu$.

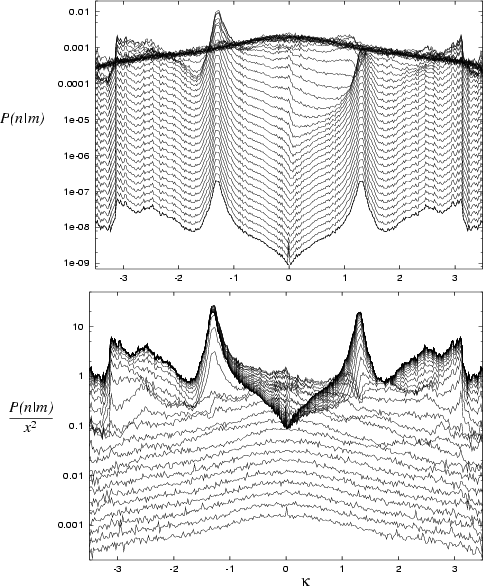
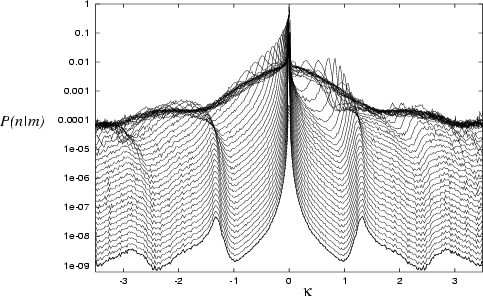
Generally, it has been found that almost any non-special deformation of the stadium creates a shape for which the RPW basis becomes much worse, and that improvement by addition of EPWs is also limited. For deformations that are localized on the perimeter, this renders the problem unsolvable if $x$ approaches $\lambda_{{\mbox{\tiny B}}}$ (de Broglie wavelength) or larger. In the above choice of deformation at $k \approx 400$ it was possible to deform from $x=0$ to $x = 10 \lambda_{{\mbox{\tiny B}}}$ with a corresponding change in typical tension from $3 \times 10^{-11}$ to $\sim 10^{-7}$. A few states of the deformed system had higher tensions of $\sim 10^{-5}$. This was acceptable for the calculation.

At each $x$, all the states in the wavenumber range $398 < k < 402$ were gathered using multiple applications of the scaling method at choices of $k$ equally spaced by $2\delta_{{\mbox{\tiny max}}} = 0.016$ in wavenumber. Thus only states falling within $\vert\delta_\mu\vert < \delta_{{\mbox{\tiny max}}}$ were kept from each scaling diagonalization. This rather small value of $\delta_{{\mbox{\tiny max}}}$ means that only about 2 states were found per diagonalization. However, because of the limitation of the basis set in such deformed shapes, this gave the highest accuracy. Because the scaling method is so fast, it did not slow down the overall computation by much (the evaluation of eigenstate values and gradients on the perimeter was the main bottleneck).

Figure 6.13: Parameter-dependent eigenvalues in the stadium billiard at $k \approx 400$. Avoided crossings are clearly visible. The parameter $x$ controlled a deformation which bent the upper straight section outwards and the curved part inwards. As a result a small integrable pocket of phase-space is created; the resulting fast-moving eigenstates become visible at the extremes of the $x$ range.

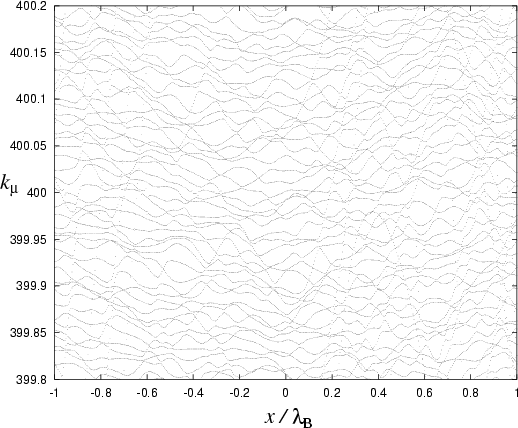To illustrate the effect of deformation on the eigenvalues, Fig. 6.13 shows their parameter-dependence under a (different) generic deformation. This was generated (to lower accuracy) by a single scaling diagonalization at each $x$ value.

Figure 6.14: Local density of states for finite rotations of the 2D quarter stadium at $k \approx 400$. Profiles of the matrix $P(n\vert m)$ are shown for 41 choices of $x$ logarithmically spaced from $x/\lambda_{{\mbox{\tiny B}}}= 10^{-3}$ to $x/\lambda_{{\mbox{\tiny B}}}= 10$ (giving the rotation angle in radians). The upper plot shows the profiles, with the FOPT result for the smallest $x$ shown as the bold dashed line. The lower plot shows the profiles divided by $x^2$, so that the breakdown of FOPT is clear.

Figure 6.15: Same as the upper plot of Fig. 6.14, except for the generic deformation explained in the text. Drift to the left is due to the lack of volume-preservation of this deformation.