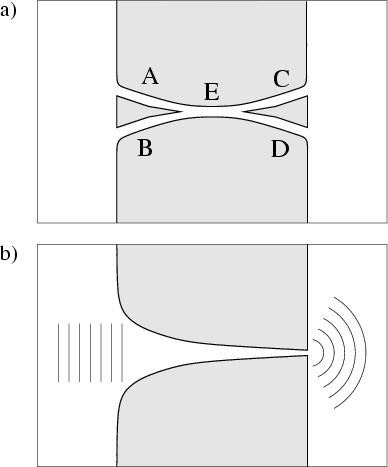
Fig. 7.3 illustrates
a
QPC-plus-reflector system
whose conductance has been experimentally measured [112].
The circular arc reflector and the vertical wall
together form a cavity which can support
long-lived resonances;
the energy of these resonances can be swept by sweeping the reflector
gate voltage.
The classical condition for stability of the cavity modes is that
the arc center must lie at, or to the left of, the wall (![]() )
[112].
The cavity modes are coupled to the left terminal via the QPC, and
to the right terminal via leakage of the modes out through the
cavity top and bottom.
The system is interesting because it is `open' in the sense that
it has no Coulomb blockade [20], but `closed' in the sense that
the dwell time is much greater than the ballistic time (the resonances are
long-lived).
It has also been studied recently in our laboratory using microwave
measurements [94,93,95].
)
[112].
The cavity modes are coupled to the left terminal via the QPC, and
to the right terminal via leakage of the modes out through the
cavity top and bottom.
The system is interesting because it is `open' in the sense that
it has no Coulomb blockade [20], but `closed' in the sense that
the dwell time is much greater than the ballistic time (the resonances are
long-lived).
It has also been studied recently in our laboratory using microwave
measurements [94,93,95].
The actual potential in a mesoscopic experiment differs from
the illustration:
it has soft walls (on the scale
![]() ),
it may have deviations from the circle due to
lithographic error, and it has modulations of the background potential
due to elastic disorder [112].
However, we will not be interested in details of the
resonator on the right-hand side.
Rather, we will adopt the view of a 2D scattering-theorist
`looking' from the left-hand side.
In this section we discuss the maximum
conductance of this system, when the `bare' QPC (i.e. without the reflector)
is in the tunneling regime (conductance
),
it may have deviations from the circle due to
lithographic error, and it has modulations of the background potential
due to elastic disorder [112].
However, we will not be interested in details of the
resonator on the right-hand side.
Rather, we will adopt the view of a 2D scattering-theorist
`looking' from the left-hand side.
In this section we discuss the maximum
conductance of this system, when the `bare' QPC (i.e. without the reflector)
is in the tunneling regime (conductance ![]() ).
).
 |
We use the slit model from the previous section to model the QPC.
This simplifies the treatment of the left-hand side scattering problem,
and we do not believe it alters the
basic conclusion.
As before, we consider the incident plus reflected wave Eq.(7.1)
when the QPC is closed to be the `unscattered'
wave.
This we expand in Bessel functions,
Now we open the slit, and replace
![]() in the above by
in the above by
![]() ,
where
,
where ![]() follows the usual definition of partial-wave phase shift [128].
The closed slit corresponds to
follows the usual definition of partial-wave phase shift [128].
The closed slit corresponds to ![]() .
An open slit leading into a closed resonator
(imagine extending the arc in Fig. 7.3 to seal off the
entire right side), in the case of infinite dephasing length,
corresponds to
.
An open slit leading into a closed resonator
(imagine extending the arc in Fig. 7.3 to seal off the
entire right side), in the case of infinite dephasing length,
corresponds to ![]() real, and would appear from the left side
as an elastic dipole scatterer.
An open slit with an open resonator
corresponds to complex
real, and would appear from the left side
as an elastic dipole scatterer.
An open slit with an open resonator
corresponds to complex ![]() with positive imaginary part,
and would appear as a general inelastic dipole scatterer.
Therefore transmission though the QPC appears,
to an observer on the left side, to be absorption of incident waves.
with positive imaginary part,
and would appear as a general inelastic dipole scatterer.
Therefore transmission though the QPC appears,
to an observer on the left side, to be absorption of incident waves.
![]() is interpreted as an `inelastic' cross section (since exiting
the right-hand terminal is equivalent to leaving in a new channel),
and
is interpreted as an `inelastic' cross section (since exiting
the right-hand terminal is equivalent to leaving in a new channel),
and
![]() as an `elastic' one.
as an `elastic' one.
![]() can be
found from integrating the net incoming flux [as in Eq.(7.5)]
of the total wavefunction on the left side.
Substitution into (7.4) then gives
can be
found from integrating the net incoming flux [as in Eq.(7.5)]
of the total wavefunction on the left side.
Substitution into (7.4) then gives
![]() .
For
.
For
![]() the maximal cross section is reached,
the maximal cross section is reached,
The associated maximum conductance is found easily
using (7.21) and (7.1) to be
How do we know that it is possible to build a resonant geometry
which corresponds to
![]() ?
The reflector can be described by
?
The reflector can be described by ![]() , the amplitude with which it returns
an outgoing p-wave back to the QPC as an incoming p-wave.
If
, the amplitude with which it returns
an outgoing p-wave back to the QPC as an incoming p-wave.
If
![]() , where the p-wave transmission of the QPC
is
, where the p-wave transmission of the QPC
is ![]() [e.g. see Eq.(7.17)], then the p-wave channel
becomes a 1D Fabry-Perot resonator with mirrors of matched
reflectivity.
Sweeping the round-trip phase then produces peaks of complete transmission
(corresponding to complete p-wave absorption on the left side).
The ratio of peak separation to peak width is the quality factor
[e.g. see Eq.(7.17)], then the p-wave channel
becomes a 1D Fabry-Perot resonator with mirrors of matched
reflectivity.
Sweeping the round-trip phase then produces peaks of complete transmission
(corresponding to complete p-wave absorption on the left side).
The ratio of peak separation to peak width is the quality factor
![]() .
Such peaks, with heights much greater than the bare tunneling QPC conductance,
were observed in the experiments
of Katine et al.[112].
However, Eq.(7.22) has not yet been tested quantitatively because
of the difficulty of matching the Fabry-Perot reflectivities in a real
2DEG experiment.
Note that the maximum conductance (7.22) also
follows immediately from
the Landauer formula, when we realize that there can be complete transmission
of the incoming
.
Such peaks, with heights much greater than the bare tunneling QPC conductance,
were observed in the experiments
of Katine et al.[112].
However, Eq.(7.22) has not yet been tested quantitatively because
of the difficulty of matching the Fabry-Perot reflectivities in a real
2DEG experiment.
Note that the maximum conductance (7.22) also
follows immediately from
the Landauer formula, when we realize that there can be complete transmission
of the incoming ![]() channel state (in Section 7.2).
channel state (in Section 7.2).
An interesting possibility arises when we realize (Appendix K)
that higher ![]() channels are still slightly transmitted by the bare QPC,
when
channels are still slightly transmitted by the bare QPC,
when ![]() , even though they are increasingly evanescent.
If the resonator has a high enough reflectivity for these modes, then
additional Fabry-Perot conductance peaks will be produced [205,38].
The peaks may be extremely narrow, but can carry a full quantum of conductance
because they can transmit another incoming
, even though they are increasingly evanescent.
If the resonator has a high enough reflectivity for these modes, then
additional Fabry-Perot conductance peaks will be produced [205,38].
The peaks may be extremely narrow, but can carry a full quantum of conductance
because they can transmit another incoming ![]() channel.
By careful arrangement of the cavity, one or more of these
peaks could be brought into conjunction with an already-existing
channel.
By careful arrangement of the cavity, one or more of these
peaks could be brought into conjunction with an already-existing
![]() peak at the Fermi energy.
(For instance, the
peak at the Fermi energy.
(For instance, the ![]() and
and ![]() resonances are in different
symmetry classes in Fig. 7.3
so there can be an exact level crossing).
Therefore, we have the surprising result that, in theory, a
conductance of
resonances are in different
symmetry classes in Fig. 7.3
so there can be an exact level crossing).
Therefore, we have the surprising result that, in theory, a
conductance of ![]() can pass through
an arbitrarily small QPC hole if
can pass through
an arbitrarily small QPC hole if ![]() resonances (from
resonances (from ![]() different channels)
coincide at the Fermi energy.
However, due to their extremely small width, such large conductance
peaks are unlikely to be observable in a real mesoscopic tunneling QPC
due to finite dephasing length and finite-temperature smearing [20].
different channels)
coincide at the Fermi energy.
However, due to their extremely small width, such large conductance
peaks are unlikely to be observable in a real mesoscopic tunneling QPC
due to finite dephasing length and finite-temperature smearing [20].
Finally, we should not overlook the fact that our expressions for
partial cross sections are a factor of 4 greater
than those conventionally arising in 2D scattering theory
from a radial potential [128,132,3,43],
because we are measuring cross section on the reflective boundary of a
semi-infinite half plane.
For instance, the maximum inelastic partial cross section for a single
channel in free space is
![]() [128,132,3,43], compared to our
maximum `inelastic'
cross section per channel Eq.(7.21).
Similarly, the maximum elastic result in free space is
[128,132,3,43], compared to our
maximum `inelastic'
cross section per channel Eq.(7.21).
Similarly, the maximum elastic result in free space is
![]() ,
compared to our maximum (normal-incidence) `elastic' cross section
per channel
,
compared to our maximum (normal-incidence) `elastic' cross section
per channel
![]() .
This latter case occurs when
.
This latter case occurs when
![]() .
.
 |