
C. Dennis Thron has called attention to the following passage from The Adventure of the Priory School, by Sir Arthur Conan Doyle:
`This track, as you perceive, was made by a rider who was going from the direction of the school.'
`Or towards it?'
`No, no, my dear Watson. The more deeply sunk impression is, of course, the hind wheel, upon which the weight rests. You perceive several places where it has passed across and obliterated the more shallow mark of the front one. It was undoubtedly heading away from the school.'
Imagine that I am steadying a bicycle to keep it from falling over, but without preventing it from moving forward or back if it decides that it wants to. The reason it might want to move is that there is a string tied to the right-hand pedal (which is to say, the right-foot pedal), which is at its lowest point, so that the right-hand crank is vertical. You are squatting behind the bike, a couple of feet back, holding the string so that it runs (nearly) horizontally from your hand forward to where it is tied to the pedal.
John Conway makes the following outrageous claim. Say that you have a group of six or more people, none of whom have thought about this problem before. You tell them the problem, and get them all to agree to the following proposal. They will each take out a dollar bill, and announce which way they think the bike will go. They will be allowed to change their minds as often as they like. When everyone has stopped waffling, you will take the dollars from those who were wrong, give some of the dollars to those who were right, and pocket the rest of the dollars yourself. You might worry that you stand to lose money if there are more right answers than wrong answers, but Conway claims that in his experience this never happens. There are always more wrong answers than right answers, and this despite the fact that you tell them in advance that there are going to be more wrong answers than right answers, and allow them to bear this in mind during the waffling process. (Or is it because you tell them that there will be more wrong answers than right answers?)
There is something funny about the way that the pedals of a bicycle screw into the cranks. One of the pedals has a normal `right-hand thread', so that you screw it in clockwise--the usual way--like a normal screw or lightbulb, and you unscrew it counter-clockwise. The other pedal has a `left-hand thread', so that it works exactly backwards: You screw it in counter-clockwise, and you unscrew it clockwise.
This `asymmetry' between the two pedals--actually it's a surfeit of symmetry we have here, rather than a dearth--is not just some whimsical notion on the part of bike manufacturers. If the pedals both had normal threads, one of them would fall out before you got to the end of the block.
If you try to figure out which pedal is the normal one using common sense, the chances are overwhelming that you will figure it out exactly wrong. If you remember this, then you're all set: Just figure it out by common sense, and then go for the opposite answer. Another good strategy is to remember that `right is right; left is wrong.'
Sometimes, when you come to put the rear wheel back on your bike after fixing a flat, or when you are fooling around trying to get the chain back onto the sprockets after it has slipped off, you may find that the chain is in the peculiar kinked configuration shown in Figure 2.
Motorcycle riders have a saying:`Push left, go left'.
A mathematical knot is a knotted loop. For example, you might take an extension cord from a drawer and plug one end into the other: this makes a mathematical knot.
It might or might not be possible to unknot it without unplugging the cord. A knot which can be unknotted is called an unknot.
Two knots are considered equivalent if it is possible to rearrange one to the form of the other, without cutting the loop and without allowing it to pass through itself. The reason for using loops of string in the mathematical definition is that knots in a length of string can always be undone, so any two lengths of string are equivalent in this sense.
If you drop a knotted loop of string on a table, it crosses over itself in a certain number of places. Possibly, there are ways to rearrange it with fewer crossings--the minimum possible number of crossings is the crossing number of the knot.
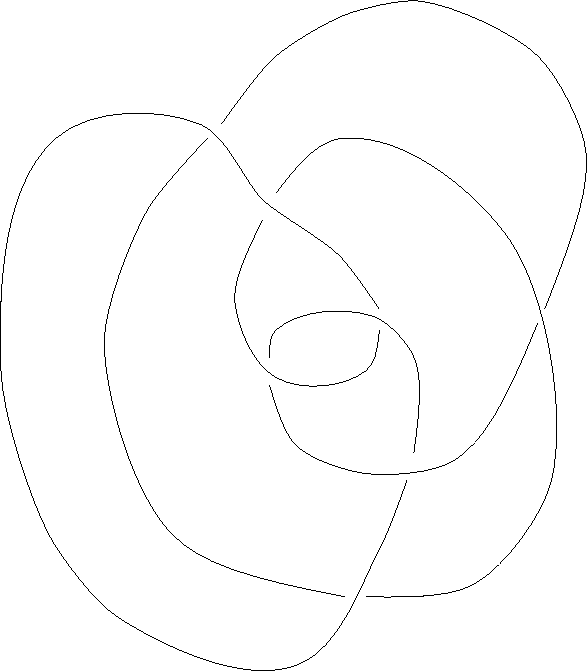 |
Make drawings and use short lengths of string to investigate the following problems.
It is a hard mathematical question to completely codify all possible knots. Given two knots, it is hard to tell whether they are the same. It is harder still to tell for sure that they are different.
Many simple knots can be arranged in a certain form, as illustrated below, which is described by a string of positive integers along with a sign.
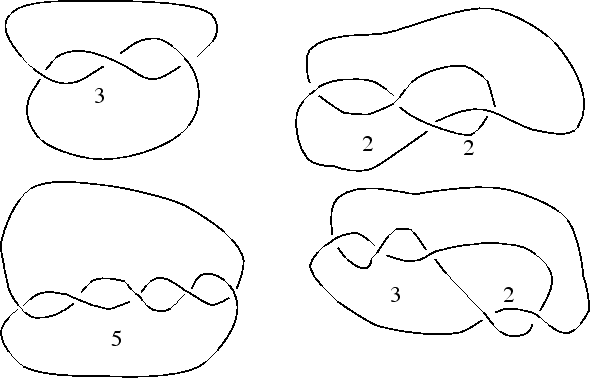 |
 |
A knot diagram gives a map on the plane, where there are four edges coming together at each vertex. Actually, it is better to think of the diagram as a map on the sphere, with a polygon on the outside. It sometimes helps in recognizing when diagrams are topologically identical to label the regions with how many edges they have.
A unicursal curve in the plane is a curve that you get when you put down your pencil, and draw until you get back to the starting point. As you draw, your pencil mark can intersect itself, but you're not supposed to have any triple intersections. You could say that you pencil is allowed to pass over an point of the plane at most twice. This property of not having any triple intersections is generic: If you scribble the curve with your eyes closed (and somehow magically manage to make the curve finish off exactly where it began), the curve won't have any triple intersections.
A unicursal curve differs from the curves shown in knot diagrams in that there is no sense of the curve's crossing over or under itself at an intersection. You can convert a unicursal curve into a knot diagram by indicating (probably with the aid of an eraser), which strand crosses over and which strand crosses under at each of the intersections.
A unicursal curve with ![]() intersections can be converted into a knot diagram
in
intersections can be converted into a knot diagram
in ![]() ways, because each intersection can be converted into a crossing
in two ways.
These 32 diagrams will not represent 32 different knots, however.
ways, because each intersection can be converted into a crossing
in two ways.
These 32 diagrams will not represent 32 different knots, however.
How do you imagine geometric figures in your head? Most people talk about their three-dimensional imagination as `visualization', but that isn't exactly right. The image you form in your head is more conceptual than a picture--you locate things in more of a three-dimensional model than in a picture. In fact, it is not easy to go from a mental image to a two-dimensional visual picture. Three-dimensional mental images are connected with your visual sense, but they are also connected with your sense of place and motion. In forming an image, it often helps to imagine moving around it, or tracing it out with your hands.
Geometric imagery is not just something that either you are born with or you are not. Like any other skill, it is something that needs to be developed with practice.
Below are some images to practice with. Some are two-dimensional, some are three-dimensional. Some are easy, some are hard, but not necessarily in numerical order. Work through these exercises in pairs. Evoke the images by talking about them, not by drawing them. It will probably help to close your eyes, although sometimes gestures and drawings in the air will help. Skip around to try to find exercises that are the right level for you.
Here are some ideas for projects. Be creative--don't feel limited by these ideas. In general, the best projects are those that students come up with on their own.
A polyhedron is the three-dimensional version of a polygon: it is a chunk of space with flat walls. In other words, it is a three-dimensional figure made by gluing polygons together. The word is Greek in origin, meaning many-seated. The plural is polyhedra. The polygonal sides of a polyhedron are called its faces.
Collect some equilateral triangles, either the snap-together plastic polydrons or paper triangles. Try gluing them together in various ways to form polyhedra.
|
A regular polygon is a polygon with all its edges equal and all angles equal. A regular polyhedron is whose faces are regular polygons, all congruent, and with the same number of polygons at each vertex.
A map in the plane is a collection of vertices and edges (possibly curved) joining the vertices such that if you cut along the edges the plane falls apart into polygons. These polygons are called the faces. A map on the sphere or any other surface is defined similarly. Two maps are considered to be the same if you can get from one to the other by a continouous motion of the whole plane. Thus the two maps in figure 8 are considered to be the same.
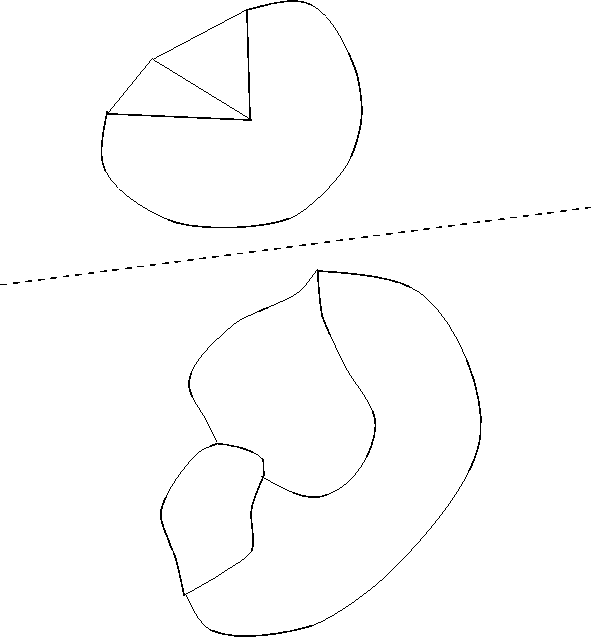 |
A map on the sphere can be represented by a map in the plane by removing a point from the sphere and then stretching the rest of the sphere out to cover the plane. (Imagine popping a balloon and stretching the rubber out onto on the plane, making sure to stretch the material near the puncture all the way out to infinity.)
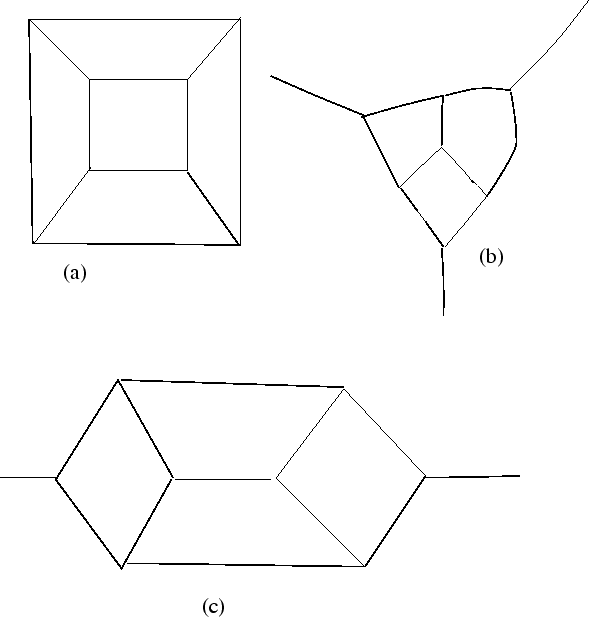 |
Depending on which point you remove from the sphere, you can get different maps in the plane. For instance, figure 9 shows three ways of representing the map depicting the edges and vertices of the cube in the plane; these three different pictures arise according to whether the point you remove lies in the middle of a face, lies on an edge, or coincides with one of the vertices of the cube.
We propose to investigate the extent to which it is true that the Euler number of a polyhedron is always equal to 2. In the course of this investigation, you will gain some experience with representing polyhedra in the plane using maps, and with drawing dual maps.
Collect, or have someone else collect, a whole bunch of polyhedra, including among them some with `holes' in them.
The dual of a map is a map you get by putting a vertex in the interior of each face, connecting the neighboring faces by new edges which cross the old edges (one new edge for each old edge), and removing all the old vertices and edges. Make sure that each new edge crosses only one old edge!
The diagram below shows three houses, each connected up to three utilities.
Topology is the theory of shapes which are allowed to stretch, compress, flex and bend, but without tearing or gluing. For example, a square is topologically equivalent to a circle, since a square can be continously deformed into a circle. As another example, a doughnut and a coffee cup with a handle for are topologically equivalent, since a doughnut can be reshaped into a coffee cup without tearing or gluing.
Here are some pictures of surfaces. The pictures are intended to indicate things like doughnuts and pretzels rather than flat strips of paper.
Recall that you get a torus by identifying the sides of a rectangle as in Figure 2.10 of SS (The Shape of Space). If you identify the sides slightly differently, as in Figure 4.3, you get a surface called a Klein bottle, shown in Figure 4.9.
Start with a different color from the one you want to make the band in. Call this the spare color. With the spare color and normal knitting needles cast on 90 stitches.
Change to your main color yarn. Knit your row of 90 stitches onto a circular needle. Your work now lies on about 2/3 of the needle. One end of the work is near the tip of the needle and has the yarn attached. This is the working end. Bend the working end around to the other end of your work, and begin to knit those stitches onto the working end, but do not slip them off the other end of the needle as you normally would. When you have knitted all 90 stitches in this way, the needle loops the work twice.
Carry on knitting in the same direction, slipping stitches off the needle
when you knit them, as normal. The needle will remain looped around the
work twice. Knit five `rows' (that is ![]() stitches) in this way.
stitches) in this way.
Cast off. You now have a Mobius band with a row of your spare color running around the middle. Cut out and remove the spare colored yarn. You will be left with one loose stitch in your main color which needs to be secured.
(Expanded by Maria Iano-Fletcher from an original recipe by Miles Reid.)
You can identify the topological type of a surface either by cutting and pasting, or by computing its invariants: Euler characteristic; orientability; number of boundary components. Use both of these methods in addressing the following problems.
Experiment with the constructions below. Put the best examples into your journal, along with comments that describe and explain what is going on. Be careful to make your examples large enough to illustrate clearly the symmetries that are present. Also make sure that your cuts are interesting enough so that extra symmetries do not creep in. Concentrate on creating a collection of examples that will get across clearly what is going on, and include enough written commentary to make a connected narrative.
Fold a sheet of paper in half, and then unfold. Cut along the fold to the center of the paper. Now wrap the paper into a conical shape, so that the cut edge lines up with the uncut half of the fold. Continue wrapping, so that the two cut edges line up and the original sheet of paper wraps two full turns around a cone. Now cut out any pattern you like from the cone. Unwrap and lay it out flat. The resulting pattern should have two-fold rotational symmetry.
Try other examples of this technique, and also try experimenting with rolling the paper more than twice around a cone.
Make or round up a strip of paper which is long compared to its width (perhaps made from ribbon, computer paper, adding-machine rolls, or formed by joining several shorter strips together end-to-end). Coil it around several times around in a Möbius band pattern. Cut out a pattern along the edge of the Möbius band, and unroll.
Given a symmetric pattern, what happens when you identify equivalent points? It gives an object with interesting topological and geometrical properties, called an orbifold.
The first instance of this is an object with bilateral symmetry, such as a (stylized) heart. Children learn to cut out a heart by folding a sheet of paper in half, and cutting out half of the pattern. When you identify equivalent points, you get half a heart.
 |
A second instance is the paper doll pattern. Here, there are two different fold lines. You make paper dolls by folding a strip of paper zig-zag, and then cutting out half a person. The half-person is enough to reconstruct the whole pattern. The quotient orbifold is a half-person, with two mirror lines.
A wave pattern is the next example. This pattern repeats horizontally, with no reflections or rotations. The wave pattern can be rolled up into a cylinder. It can be constructed by rolling up a strip of paper around a cylinder, and cutting a single wave, through several layers, with a sharp knife. When it is unrolled, the bottom part will be like the waves.
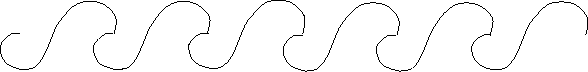 |
When a pattern repeats both horizontally and vertically, but without reflections or rotations, the quotient orbifold is a torus. You can think of it by first rolling up the pattern in one direction, matching up equivalent points, to get a long cylinder. The cylinder has a pattern which still repeats vertically. Now coil the cylinder in the other direction to match up equivalent points on the cylinder. This gives a torus.
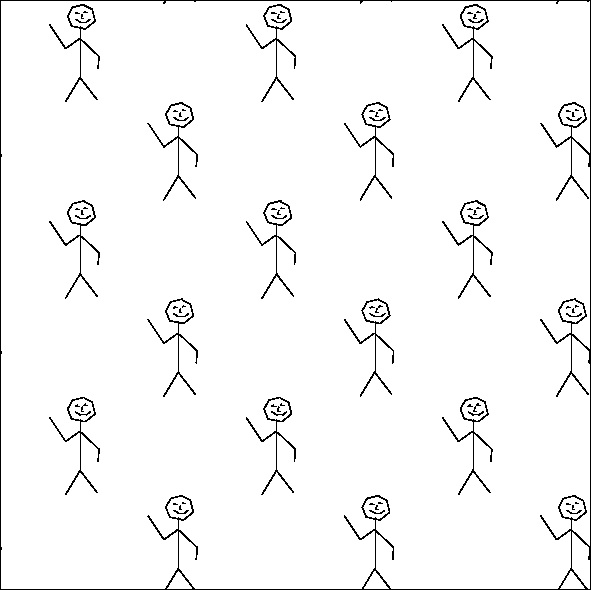 |
 |
We begin by introducing names for certain features that may occur in symmetrical patterns. To each such feature of the pattern, there is a corresponding feature of the quotient orbifold, which we will discuss later.
At a crossing point, where two or more mirrors cross,
the pattern will necessarily also have rotational symmetry.
An ![]() -way crossing point is one where precisely
-way crossing point is one where precisely ![]() mirrors meet.
At an
mirrors meet.
At an ![]() -way crossing point, adjacent mirrors meet at an angle of
-way crossing point, adjacent mirrors meet at an angle of ![]() .
(Beware: at a 2-way crossing point,
where two mirrors meet at right angles,
there will be 4 slices of pie coming together.)
.
(Beware: at a 2-way crossing point,
where two mirrors meet at right angles,
there will be 4 slices of pie coming together.)
We obtain a mirror string by starting somewhere on a mirror and walking along the mirror to the next crossing point, turning as far right as we can so as to walk along another mirror, walking to the next crossing point on it, and so on. (See figure 22.)
Suppose that you walk along a mirror string
until you first reach a point exactly like the one you started from.
If the crossings you turned at were (say)
a ![]() -way, then a
-way, then a ![]() -way, and then a
-way, and then a ![]() -way crossing,
then the mirror string would be of type
-way crossing,
then the mirror string would be of type ![]() , etc.
As a special case,
the notation
, etc.
As a special case,
the notation ![]() denotes a mirror that meets no others.
denotes a mirror that meets no others.
For example, look at a standard brick wall.
There are horizontal mirrors that each bisect a whole row of bricks,
and vertical mirrors that pass through bricks and cement
alternately.
The crossing points, all 2-way, are of two kinds:
one at the center of a brick,
one between bricks.
The mirror strings have four corners,
and you might expect that their type would be ![]() .
However, the correct type is
.
However, the correct type is ![]() .
The reason is that after going only half way round, we come to a point
exactly like our starting point.
.
The reason is that after going only half way round, we come to a point
exactly like our starting point.
For example, on our brick wall there is an order 2 gyration point in the middle of the rectangle outlined by any mirror string.
A symmetry group is the collection of all symmetry operations of a pattern. We give the same names to symmetry groups as to the corresponding quotient orbifolds.
We regard every orbifold as obtained from a sphere by adding cone-points,
mirror boundaries,
handles, and cross-caps.
The major part of the notation enumerates
the orders of the distinct cone points,
and then the types of all the different mirror boundaries.
An initial black spot ![]() indicates the addition of a handle;
a final circle
indicates the addition of a handle;
a final circle ![]() the addition of a cross cap.
the addition of a cross cap.
For example, our brick wall gives ![]() ,
corresponding to its gyration point of order 2,
and its mirror string with two 2-way corners.
,
corresponding to its gyration point of order 2,
and its mirror string with two 2-way corners.
Here are the types of some of the patterns shown in section 31:
Figure 16: ![]() ;
Figure 17:
;
Figure 17: ![]() ;
Figure 18:
;
Figure 18: ![]() ;
Figure 19:
;
Figure 19: ![]() .
Figure 20:
.
Figure 20: ![]() .
Figure 21:
.
Figure 21: ![]() .
.
Apart from the spots and circles, these can be read directly
from the pictures. The important thing to remember is that if
two things are equivalent by a symmetry, then you only record
one of them.
A dodecahedron is very like a sphere.
The orbifold corresponding to its symmetry group is a
spherical triangle having angles
![]() ;
so its symmetry group is
;
so its symmetry group is ![]() .
.
You, the topologically spherical reader,
approximately have symmetry group ![]() ,
because the quotient orbifold of a sphere by a single reflection
is a hemisphere whose mirror boundary has no corners.
,
because the quotient orbifold of a sphere by a single reflection
is a hemisphere whose mirror boundary has no corners.
The Orbifold Shop has gone into the business of installing orbifold parts. They offer a special promotional deal: a free coupon for $2.00 worth of parts, installation included, to anyone acquiring a new orbifold.
There are only a few kinds of features for two-dimensional orbifolds, but they can be used in interesting combinations.
With the ![]() coupon, for example, you could order an orbifold with
four order
coupon, for example, you could order an orbifold with
four order ![]() cone points, costing
cone points, costing ![]() each. Or, you could order
an order
each. Or, you could order
an order ![]() cone point costing
cone point costing ![]() , a mirror costing
, a mirror costing ![]() ,
and an order
,
and an order ![]() corner reflector costing
corner reflector costing ![]() .
.
Theorem.
If you exactly spend your coupon at the Orbifold Shop, you will have
a quotient orbifold coming from a symmetrically repeating
pattern in the Euclidean plane with a bounded fundamental domain.
There are exactly ![]() different ways to do this, and corresponding
to the
different ways to do this, and corresponding
to the ![]() different symmetrically repeating patterns with bounded
fundamental domain in the Euclidean plane.
different symmetrically repeating patterns with bounded
fundamental domain in the Euclidean plane.
 |
Suppose we have a symmetric pattern in the plane. We can make a symmetric map by subdividing the quotient orbifold into polygons, and then `unrolling it' or `unfolding it' to get a map in the plane.
If we look at a large area ![]() in the plane, made up from
in the plane, made up from ![]() copies of a
fundamental domain, then each face in the map on the quotient orbifold
contributes
copies of a
fundamental domain, then each face in the map on the quotient orbifold
contributes ![]() faces to the region. An edge which is not on a mirror
also contributes approximately
faces to the region. An edge which is not on a mirror
also contributes approximately ![]() copies -- approximately, because when
it is on the boundary of
copies -- approximately, because when
it is on the boundary of ![]() , we don't quite know how to match
it with a fundametnal region.
, we don't quite know how to match
it with a fundametnal region.
In general, if an edge or point has order ![]() symmetry which
which preserves it, it contributes approximately
symmetry which
which preserves it, it contributes approximately ![]() copies of
itself to
copies of
itself to ![]() , since each time it occurs, as long as it is not on
the boundary of
, since each time it occurs, as long as it is not on
the boundary of ![]() , it is counted in
, it is counted in ![]() copies of the fundamental domain.
copies of the fundamental domain.
Thus,
Definition.
The orbifold Euler characteristic is ![]() , where each
vertex and edge is given weight
, where each
vertex and edge is given weight ![]() , where
, where ![]() is the order of symmetry
which preserves it.
is the order of symmetry
which preserves it.
It is important to keep in mind the distinction between the topological
Euler characteristic and the orbifold Euler characteristic. For instance,
consider the billiard table orbifold, which is just a rectangle.
In the orbifold Euler characteristic,
the four corners each count ![]() , the four edges count
, the four edges count ![]() , and the
face counts
, and the
face counts ![]() , for a total of
, for a total of ![]() . In contrast, the
topological Euler characteristic
is
. In contrast, the
topological Euler characteristic
is ![]() .
.
Theorem.
The quotient orbifold of any symmetry pattern in the Euclidean plane
which has a bounded fundamental region has orbifold Euler number ![]() .
.
Sketch of proof: take a large area in the plane that is topologically
a disk. Its Euler characteristic is ![]() . This is approximately
equal to
. This is approximately
equal to ![]() times the orbifold Euler characteristic, for some large
times the orbifold Euler characteristic, for some large ![]() ,
so the orbifold Euler characteristic must be
,
so the orbifold Euler characteristic must be ![]() .
.
How do the people at The Orbifold Shop figure its prices?
The cost is based on the orbifold Euler characteristic: it costs
![]() to lower the orbifold Euler characteristic by 1.
When they install a fancy new part, they calculate the difference between
the new part and the part that was traded in.
to lower the orbifold Euler characteristic by 1.
When they install a fancy new part, they calculate the difference between
the new part and the part that was traded in.
For instance, to install
a cone point, they remove an ordinary point. An ordinary point counts ![]() ,
while an order
,
while an order ![]() cone point counts
cone point counts ![]() , so the difference is
, so the difference is ![]() .
.
To install a handle, they arrange a map on the original orbifold so that it
has a square face. They remove the square, and identify opposite edges
of it. This identifies all four vertices to a single vertex. The net
effect is to remove ![]() face, remove
face, remove ![]() edges (since
edges (since ![]() are reduced to
are reduced to ![]() ),
and to remove
),
and to remove ![]() vertices. The effect on the orbifold Euler characteristic
is to subtract
vertices. The effect on the orbifold Euler characteristic
is to subtract ![]() , so the cost is
, so the cost is ![]() .
.
To complete the connection between orbifold Euler characteristic and
symmetry patterns, we would have to verify that each of the possible
configurations of parts with orbifold Euler characteristic ![]() actually
does come from a symmetry pattern in the plane. This can be done in
a straightforward way by explicit constructions. It is illuminating
to see a few representative examples, but it is not very illuminating
to see the entire exercise unless you go through it yourself.
actually
does come from a symmetry pattern in the plane. This can be done in
a straightforward way by explicit constructions. It is illuminating
to see a few representative examples, but it is not very illuminating
to see the entire exercise unless you go through it yourself.
A symmetry pattern on the sphere always gives rise to a quotient orbifold
with positive Euler characteristic. In fact, if the order of symmetry is
![]() , then the Euler characteristic of the quotient orbifold is
, then the Euler characteristic of the quotient orbifold is ![]() ,
since the Euler characteristic of the sphere is
,
since the Euler characteristic of the sphere is ![]() .
.
However, the converse is not true. Not every collection of parts costing
less than ![]() can be put together to make a viable pattern for
symmetry on the sphere. Fortunately, the experts at The Orbifold Shop
know the four bad configurations which are too skimpy to be viable:
can be put together to make a viable pattern for
symmetry on the sphere. Fortunately, the experts at The Orbifold Shop
know the four bad configurations which are too skimpy to be viable:
All other configurations are good. If they form an orbifold with positive orbifold Euler characteristic, they come from a pattern of symmetry on the sphere.
The situation for negative orbifold Euler characteristic is straightforward,
but we will not prove it:
Theorem. Every orbifold with negative orbifold Euler characteristic comes from a pattern of symmetry in the hyperbolic plane with bounded fundamental domain. Every pattern of symmetry in the hyperbolic plane with compact fundamental domain gives rise to a quotient orbifold with negative orbifold Euler characteristic.
Since you can spend as much as you want, there are an infinite number of these.
In this section, we will give some hints about how to learn to classify the patterns. However, we want to emphasize that this is a tricky business, and the only way to learn it is by hard work. As usual, when you analyze a pattern, you should look first for the mirror strings. The information in this section is meant as a way that you can learn to become more familiar with the 17 types of patterns, in a way that will help you to distinguish between them more quickly, and perhaps in some cases to be able to classify some of the more complicated patterns without seeing clearly and precisely what the quotient is. This kind of superficial knowledge is no substitute for a real visceral understanding of what the quotient orbifold is, and in every case you should go on and try to understand why the pattern is what you say it is while your friends are busy admiring your cleverness.
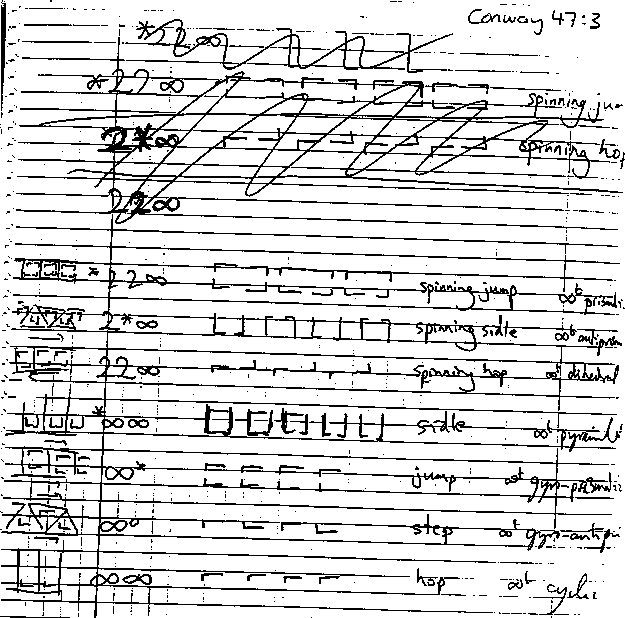
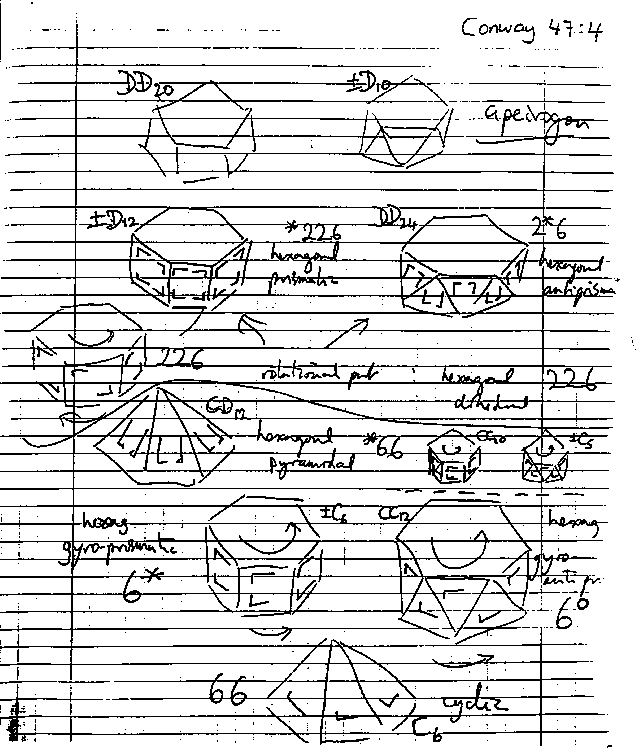
This information presented in this section has been gleaned from a cryptic manuscript discovered among the personal papers of John Conway after his death. For each of the 17 types of patterns, the manuscript shows a small piece of the pattern, the notation for the quotient orbifold, and Conway's idiosyncratic pidgin-Greek name for the corresponding pattern. These names are far from standard, and while they are unlikely ever to enter common use, we have found from our own experience that they are not wholly useless as a method for recognizing the patterns.
We will begin by discussing Conway's names for the orbifolds. A reproduction of Conway's manuscript appears at the end of the section. You should refer to the reproduction as you try to understand the basis for the names.
For example, if you are looking at a standard brick wall, it will look essentially the same whether you stand on your feet or on your head. This will be true even if the courses of bricks in the wall do not run parallel to the ground, as they invariably do. Thus you can recognize right away that the brick-wall pattern is di-something-or-other In fact, it is dirhombic.
Another way to think about this is that if you could manage to turn the brick wall upside down, you wouldn't notice the difference. Again, this would be true even if you kept your head tilted to one side. More to the point, try looking at a dirhombic pattern drawn on a sheet of paper. Place the paper at an arbitrary angle, note what the pattern looks like in the large, and rotate the pattern around until it looks in the large like it did to begin with. When this happens, you will have turned the paper through half a rev. No matter how the pattern is tilted originally, there is always one and only one other direction from which it appear the same in the large.
This `in the large' business means that you are not supposed to notice if, after twisting the paper around, the pattern appears to have been shifted by a translation. You don't have to go grubbing around looking for some pesky little point about which to rotate the pattern. Just take the wide, relaxed view.
The scopic patterns are those that emerge from kaleidoscopes:
![]() hexascopic;
hexascopic;
![]() tetrascopic;
tetrascopic;
![]() triscopic;
triscopic;
![]() discopic;
discopic;
![]() monoscopic;
monoscopic;
Their ![]() -less counterparts
are the tropic patterns (from the Greek for `turn'):
-less counterparts
are the tropic patterns (from the Greek for `turn'):
![]() hexatropic;
hexatropic;
![]() tetratropic;
tetratropic;
![]() tritropic;
tritropic;
![]() ditropic;
ditropic;
![]() monotropic.
monotropic.
With the scopic patterns, it's all done with mirrors,
while with the tropic patterns,
it's all done with gyration points.
The two exceptions are:
![]() monoscopic;
monoscopic;
![]() monotropic.
There is evidence that Conway did not consider these
to be exceptions, on the grounds that
`with the scopics it's all done with mirrors and translations,
while with the tropics,
it's all done with turnings and translations'.
monotropic.
There is evidence that Conway did not consider these
to be exceptions, on the grounds that
`with the scopics it's all done with mirrors and translations,
while with the tropics,
it's all done with turnings and translations'.
The gyro patterns contain both mirrors and gyration points:
![]() tetragyro;
tetragyro;
![]() trigyro;
trigyro;
![]() digyro.
digyro.
Since both tropic and gyro patterns involve gyration points, there is a real possibility of confusing the names. Strangely, it is the tropic patterns that are the more closely connected to gyration points. In practice, it seems to be easy enough to draw this distinction correctly, probably because the tropics correspond closely to the scopics, and `tropic' rhymes with `scopic'. Conway's view appears to have been that a gyration point, which is a point of rotational symmetry that does NOT lie on a mirror, becomes ever so much more of a gyration point when there are mirrors around that it might have been tempted to lie on, and that therefore patterns that contain both gyration points and mirrors are more gyro than patterns with gyration points but no mirrors.
The glide patterns involve glide-reflections:
![]() diglide;
diglide;
![]() monoglide.
monoglide.
The glide patterns are the hardest to recognize. The quotient orbifold of the diglide pattern is a projective plane with two cone points; the quotient of the monoglide patterns is a Klein bottle. When you run up against one of these patterns, you just have to sweat it out. One trick is that when you meet something that has glide-reflections but not much else, then you decide that it must be either a diglide or a monoglide, and you can distinguish between them by deciding whether it's a di- or a mono- pattern, which is a distinction that is relatively easy to make. Another clue to help distinguish these two cases is that a diglide pattern has glides in two different directions, while a monoglide has glides in only one direction. Yet another clue is that in a monoglide you can often spot two disjoint Möbius strips within the quotient orbifold, corresponding to the fact that the quotient orbifold for a monoglide pattern is a Klein bottle, which can be pieced together from two Möbius strips. These two disjoint Möbius strips arise from the action of glide-reflections along parallel but inequivalent axes.
The rhombic patterns often give a feeling of rhombosity:
![]() dirhombic;
dirhombic;
![]() monorhombic.
monorhombic.
An ordinary brick wall is dirhombic; it can be made monorhombic by breaking the gyrational symmetry. The quotient of a monorhombic pattern is a Möbius strip. Like the two glide quotients, it is non-orientable, but it is much easier to identify because of the presence of the mirrors.
Another hint is to keep your eyes open for symmetrical patterns in the world around you. When you see a pattern, copy it onto a flashcard, even if you cannot analyze it immediately. When you have determined the correct analysis, write it on the back and add it to your deck.



We want to explore some aspects of geometry on the surface of the sphere. This is an interesting subject in itself, and it will come in handy later on when we discuss Descartes's angle-defect formula.
Great circles on the sphere are the analogs of straight lines in the plane. Such curves are often called geodesics. A spherical triangle is a region of the sphere bounded by three arcs of geodesics.
A proof of the area formula can be found in Chapter 9 of Weeks, The Shape of Space.
The angle defect at a vertex of a polygon is defined to be ![]() minus the sum of the angles at the corners of the faces at that vertex.
For instance, at any vertex of a cube there are three angles of
minus the sum of the angles at the corners of the faces at that vertex.
For instance, at any vertex of a cube there are three angles of ![]() ,
so the angle defect is
,
so the angle defect is ![]() . You can visualize the angle defect by
cutting along an edge at that vertex, and then flattening out a neighborhood
of the vertex into the plane. A little gap will form where the slit is:
the angle by which it opens up is the angle defect.
. You can visualize the angle defect by
cutting along an edge at that vertex, and then flattening out a neighborhood
of the vertex into the plane. A little gap will form where the slit is:
the angle by which it opens up is the angle defect.
The total angle defect of the polyhedron is gotten by adding up the
angle defects at all the vertices of the polyhedron. For a cube,
the total angle defect is
![]() .
.
The angle defect at a vertex of a polygon was defined to be the amount
by which the sum of the angles at the corners of the faces at that vertex
falls short of ![]() and the total angle defect of the polyhedron was defined to be what one got when one added up the
angle defects at all the vertices of the polyhedron.
We call the total defect
and the total angle defect of the polyhedron was defined to be what one got when one added up the
angle defects at all the vertices of the polyhedron.
We call the total defect ![]() .
Descartes discovered that there is a connection between the total defect,
.
Descartes discovered that there is a connection between the total defect, ![]() , and the Euler Number
, and the Euler Number ![]() . Namely,
. Namely,
| (1) |
Here are two proofs. They both use the fact that the sum of the
angles of a polygon with ![]() sides is
sides is ![]() .
.
We will try to cancel out the terms as much as possible, by grouping within polygons.
For each edge, there is ![]() to allocate. An edge has a polygon on
each side: put
to allocate. An edge has a polygon on
each side: put ![]() on one side, and
on one side, and ![]() on the other.
on the other.
For each vertex, there is ![]() to allocate: we will do it according to
the angles of polygons at that vertex. If the angle of a polygon at
the vertex is
to allocate: we will do it according to
the angles of polygons at that vertex. If the angle of a polygon at
the vertex is ![]() , allocate
, allocate ![]() of the
of the ![]() to that polygon.
This leaves something at the vertex: the angle defect.
to that polygon.
This leaves something at the vertex: the angle defect.
In each polygon, we now have a total of the sum of its angles minus
![]() (where
(where ![]() is the number of sides) plus
is the number of sides) plus ![]() . Since
the sum of the angles of any polygon is
. Since
the sum of the angles of any polygon is ![]() , this is
, this is ![]() .
Therefore,
.
Therefore,
We begin to compute:
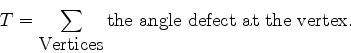


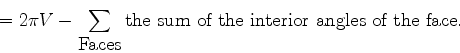
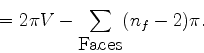
If you take a flat piece of paper and bend it gently, it bends in only one direction at a time. At any point on the paper, you can find at least one direction through which there is a straight line on the surface. You can bend it into a cylinder, or into a cone, but you can never bend it without crumpling or distorting to the get a portion of the surface of a sphere.
If you take the skin of a sphere, it cannot be flattened out into the plane without distortion or crumpling. This phenomenon is familiar from orange peels or apple peels. Not even a small area of the skin of a sphere can be flattened out without some distortion, although the distortion is very small for a small piece of the sphere. That's why rectangular maps of small areas of the earth work pretty well, but maps of larger areas are forced to have considerable distortion.
The physical descriptions of what happens as you bend various surfaces without distortion do not have to do with the topological properties of the surfaces. Rather, they have to do with the intrinsic geometry of the surfaces. The intrinsic geometry has to do with geometric properties which can be detected by measurements along the surface, without considering the space around it.
There is a mathematical way to explain the intrinsic geometric property of a surface that tells when one surface can or cannot be bent into another. The mathematical concept is called the Gaussian curvature of a surface, or often simply the curvature of a surface. This kind of curvature is not to be confused with the curvature of a curve. The curvature of a curve is an extrinsic geometric property, telling how it is bent in the plane, or bent in space. Gaussian curvature is an intrinsic geometric property: it stays the same no matter how a surface is bent, as long as it is not distorted, neither stretched or compressed.
To get a first qualitative idea of how curvature works, here are some examples.
A surface which bulges out in all directions, such as the surface of a sphere, is positively curved. A rough test for positive curvature is that if you take any point on the surface, there is some plane touching the surface at that point so that the surface lies all on one side except at that point. No matter how you (gently) bend the surface, that property remains.
A flat piece of paper, or the surface of a cylinder or cone, has ![]() curvature.
curvature.
A saddle-shaped surface has negative curvature: every plane through a point on the saddle actually cuts the saddle surface in two or more pieces.
Gaussian curvature is a numerical quantity associated to an area of a surface, very closely related to angle defect. Recall that the angle defect of a polyhedron at a vertex is the angle by which a small neighborhood of a vertex opens up, when it is slit along one of the edges going into the vertex.
The total Gaussian curvature of a region on a surface is the angle by which
its boundary opens up, when laid out in the plane. To actually measure
Gaussian curvature of a region bounded by a curve,
you can cut out a narrow strip on the surface in neighborhood of the
bounding curve. You also need to cut open the curve, so it will be
free to flatten out. Apply it to a flat surface, being careful to
distort it as little as possible. If the surface is positively curved
in the region inside the curve, when you flatten it out, the curve will
open up. The angle between the tangents to the curve at the two sides
of the cut is the total Gaussian curvature. This is like angle defect:
in fact, the total curvature of a region of a polyhedron containing exactly
one vertex is the angle defect at that vertex. You must pay attention
not just to the angle between the ends of the strip, but
how the strip curled around,
keeping in mind that the standard for zero curvature is
a strip which comes back and meets itself. Pay attention to ![]() 's and
's and
![]() 's.
's.
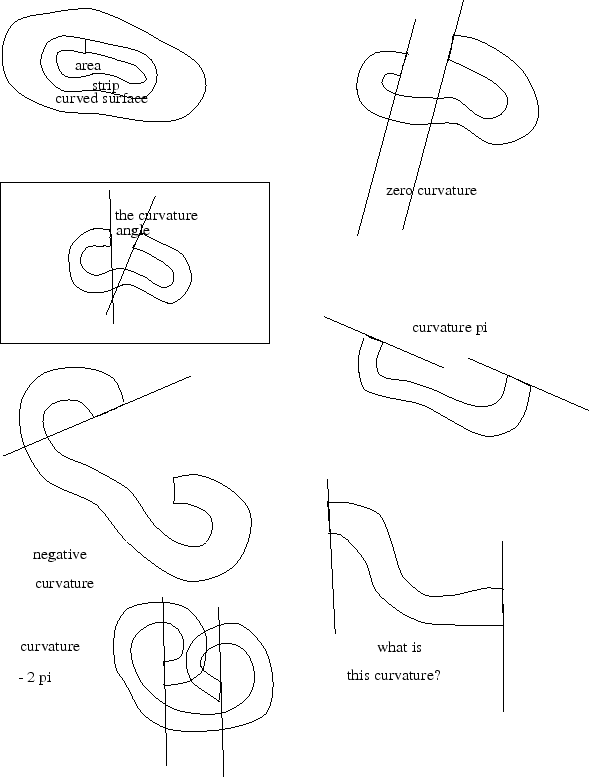 |
If the total curvature inside the region is negative, the strip will curl around further than necessary to close. The curvature is negative, and is measured by the angle by which the curve overshoots.
A less destructive way to measure total Gaussian curvature of a region is to apply narrow strips of paper to the surface, e.g., masking tape. They can be then be removed and flattened out in the plane to measure the curvature.
The total curvature of any surface topologically equivalent to the sphere
is ![]() .
This can be seen very simply
from the definition of the curvature of a region
in terms of the angle of rotation when the surface
is rolled around on the plane;
the only problem is the perennial one of
keeping proper track of multiples of
.
This can be seen very simply
from the definition of the curvature of a region
in terms of the angle of rotation when the surface
is rolled around on the plane;
the only problem is the perennial one of
keeping proper track of multiples of ![]() when measuring the angle of
rotation.
Since are trying to show that the total curvature is a specific multiple of
when measuring the angle of
rotation.
Since are trying to show that the total curvature is a specific multiple of
![]() ,
this problem is crucial.
So to begin with let's think carefully about
how to reckon these angles correctly
,
this problem is crucial.
So to begin with let's think carefully about
how to reckon these angles correctly
Let the clocks be labelled ![]() ,
, ![]() ,
, ![]() , ....
To start off, we set all the clocks to 0 o'clock.
(little hand on the 0; big hand on the 0),
Now we set clock
, ....
To start off, we set all the clocks to 0 o'clock.
(little hand on the 0; big hand on the 0),
Now we set clock ![]() ahead half an hour
so that it now the time it tells is 0:30
(little hand on the 0 (as they say); big hand on the 6).
What angle does its big hand make with that of clock
ahead half an hour
so that it now the time it tells is 0:30
(little hand on the 0 (as they say); big hand on the 6).
What angle does its big hand make with that of clock ![]() ?
Or rather, through what angle has its big hand moved relative to that
of clock
?
Or rather, through what angle has its big hand moved relative to that
of clock ![]() ?
The angle is
?
The angle is ![]() .
If instead of degrees or radians, we measure our angles in revs
(short for revolutions),
then the angle is
.
If instead of degrees or radians, we measure our angles in revs
(short for revolutions),
then the angle is ![]() rev.
We could also say that the angle is
rev.
We could also say that the angle is ![]() hour:
as far as the big hand of a clock is concerned,
an hour is the same as a rev.
hour:
as far as the big hand of a clock is concerned,
an hour is the same as a rev.
Now take clock ![]() and set it to 1:00.
Relative to the big hand of clock
and set it to 1:00.
Relative to the big hand of clock ![]() , the big hand of
, the big hand of ![]() has moved
through an angle of
has moved
through an angle of ![]() , or 1 rev, or 1 hour.
Relative to the big hand of
, or 1 rev, or 1 hour.
Relative to the big hand of ![]() , the big hand of
, the big hand of ![]() has moved through
an angle of
has moved through
an angle of ![]() , or
, or ![]() rev.
Relative to the big hand of
rev.
Relative to the big hand of ![]() , the big hand of
, the big hand of ![]() has moved through
an angle of
has moved through
an angle of ![]() , or
, or ![]() rev,
and the big hand of
rev,
and the big hand of ![]() has moved
has moved ![]() , or
, or ![]() rev.
rev.
To begin with, let's designate the two ends of the strip
as the left end and the right end in such a way that
traversing the strip from the left end to the right end
corresponds to circling clockwise around the region.
We begin by fixing the left-hand end of the strip to the wall so that
the straight edge of the cut at the left end of the strip--the cut that
we made to convert the band into a strip--runs
straight up and down, parallel to the big hand of clock ![]() ,
and so that the strip runs off toward the right.
Now we move from left to right along the strip,
i.e. clockwise around the boundary of the region,
fixing the strip so that
it lies as flat as possible, until we come to the right end of the strip.
Then we look at the cut bounding the right-hand end of the strip,
and see how far it has turned relative to the left-hand end of the strip.
Since we were so careful in laying out the left-hand end of the strip,
our task in reckoning the angle of the right-hand end of the strip
amounts to deciding what time you get if you think of the right-hand end
of the strip as the big hand of a clock.
The curvature inside the region will correspond to the amount by which the time
told by the right-hand end of the strip falls short of 1:00.
,
and so that the strip runs off toward the right.
Now we move from left to right along the strip,
i.e. clockwise around the boundary of the region,
fixing the strip so that
it lies as flat as possible, until we come to the right end of the strip.
Then we look at the cut bounding the right-hand end of the strip,
and see how far it has turned relative to the left-hand end of the strip.
Since we were so careful in laying out the left-hand end of the strip,
our task in reckoning the angle of the right-hand end of the strip
amounts to deciding what time you get if you think of the right-hand end
of the strip as the big hand of a clock.
The curvature inside the region will correspond to the amount by which the time
told by the right-hand end of the strip falls short of 1:00.
For instance, say the region ![]() is a tiny disk in the Euclidean plane.
When we cut a strip from its boundary and lay it out as described above,
the time told by its right hand end will be precisely 1:00, so the curvature
of
is a tiny disk in the Euclidean plane.
When we cut a strip from its boundary and lay it out as described above,
the time told by its right hand end will be precisely 1:00, so the curvature
of ![]() will be exactly 0.
If
will be exactly 0.
If ![]() is a tiny disk on the sphere, then when the strip is laid out the time
told will be just shy of 1:00, say 0:59, and the curvature of the region
will be
is a tiny disk on the sphere, then when the strip is laid out the time
told will be just shy of 1:00, say 0:59, and the curvature of the region
will be ![]() rev, or
rev, or
![]() .
.
When the region ![]() is the lower hemisphere of a round sphere,
the strip you get will be laid out in a straight line,
and the time told by the right-hand end will be 0:00,
so the total curvature will be
is the lower hemisphere of a round sphere,
the strip you get will be laid out in a straight line,
and the time told by the right-hand end will be 0:00,
so the total curvature will be ![]() rev, i.e.
rev, i.e. ![]() .
The total curvature of the upper hemisphere is
.
The total curvature of the upper hemisphere is ![]() as well,
so that the total curvature of the sphere is
as well,
so that the total curvature of the sphere is ![]() .
.
Another way to see that the total curvature of the sphere is ![]() is to take as the region
is to take as the region ![]() the outside of a small circle on the
sphere.
When we lay out a strip following the prescription above, being sure to
traverse the boundary of the region
the outside of a small circle on the
sphere.
When we lay out a strip following the prescription above, being sure to
traverse the boundary of the region ![]() in the clockwise sense as viewed
from the point of view of the region
in the clockwise sense as viewed
from the point of view of the region ![]() , we see that the time told by the
right hand end of the strip is very nearly
, we see that the time told by the
right hand end of the strip is very nearly ![]() o'clock!
The precise time will be just shy of this,
say
o'clock!
The precise time will be just shy of this,
say ![]() :59,
and the total curvature of the region will then be
:59,
and the total curvature of the region will then be
![]() revs.
Taking the limit,
the total curvature of the sphere is
revs.
Taking the limit,
the total curvature of the sphere is ![]() revs, or
revs, or ![]() .
.
But this last argument will work equally well on any surface topologically
equivalent to a sphere, so any such surface has total curvature ![]() .
.
What gives is the lemma that states that if you take a disklike region ![]() and divide it into two disklike subregions
and divide it into two disklike subregions ![]() and
and ![]() , then the
curvature inside
, then the
curvature inside ![]() when measured by laying out its boundary is the sum
of the curvatures inside
when measured by laying out its boundary is the sum
of the curvatures inside ![]() and
and ![]() measured in this way.
This lemma might seem like a tautology.
Why should there be anything to prove here?
How could it fail to be the case that the curvature inside the whole is
the sum of the curvatures inside the parts?
The answer is,
it could fail to be the case by virtue of our having given a faulty definition.
When we define the curvature inside a region, we have to make sure that the
quantity we're defining has the additivity property, or the definition is no
good.
Simply calling some quantity the curvature inside the region will not make
it have this additivity property.
For instance, what if we had defined the curvature inside a region to be
measured in this way.
This lemma might seem like a tautology.
Why should there be anything to prove here?
How could it fail to be the case that the curvature inside the whole is
the sum of the curvatures inside the parts?
The answer is,
it could fail to be the case by virtue of our having given a faulty definition.
When we define the curvature inside a region, we have to make sure that the
quantity we're defining has the additivity property, or the definition is no
good.
Simply calling some quantity the curvature inside the region will not make
it have this additivity property.
For instance, what if we had defined the curvature inside a region to be
![]() , no matter what the region?
More to the point, what if in the definition of the curvature inside
a region we had forgotten the proviso that the region
, no matter what the region?
More to the point, what if in the definition of the curvature inside
a region we had forgotten the proviso that the region ![]() be disklike?
Think about it.
be disklike?
Think about it.