3.6 Optimization: Quiz
Problem 3
A typical aluminum can made to hold 12 ounces (about 350 grams) of soda or another liquid is shaped as a cylinder, has dimensions radius = r and height = h, and weighs about 12 grams. It is assumed to be uniformly constructed, so when the can is full, its center of mass is in the middle of the can. When the can is gradually emptied, the center of mass drops as the liquid drops. When the can is empty, its center of mass is once more in the middle of the can.
What is the lowest point reached by the center of mass during the emptying of the can?
Answers, problem 3
Let y be the height of the soda in the can. The center of mass x of the can should be thought of as a function of y, and will depend only on the height of the soda and the height h of the can:
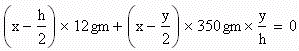
Solve for x and find y that minimizes x.

The graph shows the center of mass as a function of the height of soda in the can.

The lowest center of mass is attained when