Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

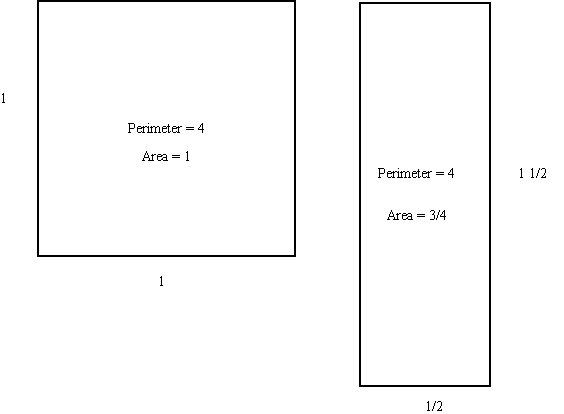
Contents In this lecture we learn to maximize or minimize a function on an interval by solving what are called "optimization problems." Quick Question Among all the rectangles with perimeter equal to 4, which one has the largest area? Answer Textbook Optimization Today's Homework Log into WebWorK Quiz Optimization Quiz Examples You want to run an underground power cable from a power station on one side of a river to a house on the other side. The house is 5 miles downstream from the station, and the river has a constant width of 1 mile. It costs $1000 per mile to lay cable underground, and $3000 per mile to lay cable under water. How should you lay the cable to minimize the total cost, and what will the minimum cost be? You want to smuggle a precious metal out of the country, by disguising it as a single cylindrical barrel, closed at both ends. The cost of shipping is $7 per cubic foot. Once out the the country, you can sell the metal for $8 per square foot. Assuming that you design the barrels with the height equal to twice the diameter, how many square feet should you smuggle, and what will your profit be? A wire 50 inches long is cut into two pieces. One piece is bent into a circle; the other, into a square. Where should the wire be cut to minimize the sum of the areas of the two shapes? Applets Optimization Videos Find the open box of largest volume that can be built from a 24" x 20" rectangle by removing squares from the corners. Sketch the rectangle to understand the problem Experiment with different size boxes The solution using calculus Farmer Maria wishes to enclose the maximum area of pasture in a rectangle. One side of the pasture is already fenced. She has 100 feet of fence left. What dimensions should she make her field? Visualize the problem with different rectangles The solution using calculus

Lecture 28 | Index | Lecture 30