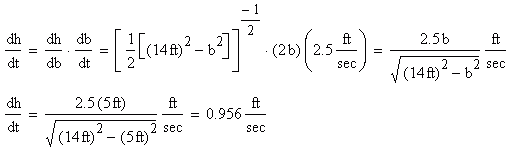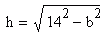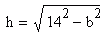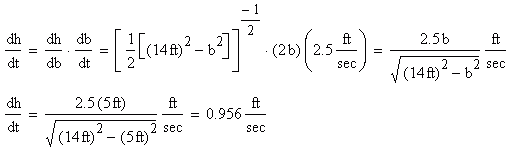Related Rates: Quiz
Problem 3
A 14-foot ladder rests vertically against the side of a house. An absent-minded worker begins dragging the bottom of the ladder away from the house at a rate of 2.5 feet per second, not noticing that another worker is standing at the top of the ladder. After a delayed reaction of 2 seconds, the worker on the ladder yells out. How fast is he moving down the wall when he yells?
Answers, problem 3
Let h = the height of the top of the ladder on the wall, b = the distance of the bottom of the ladder away from the wall. h and b are related by the equation
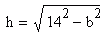
To find how fast the top of the ladder is moving, dh/dt, we can use the chain rule, with db/dt = 2.5 ft/sec: