Slope Fields and Euler's Method: Quiz

Problem 3

using Euler's Method.

Answers, problem 3

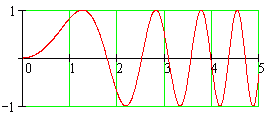
If we knew an antiderivative S(u) for sin(u²), we could use it and compute y(x) = S(x) − S(0). However, there is no such nice antiderivative, so we look at the problem another way: such a solution S would satisfy the initial-value problem y(0) = 0, y′ = sin(x²) − sin(0) = sin(x²). Therefore, evaluating the integral is equivalent to finding the y(x) for a particular x. Since we have a differential equation and starting point, we can use Euler's Method to estimate the value of y at x.

Next ≈ Previous ≈ Up