Issues in Curve Sketching: Quiz

Problem 1

Identify local and absolute maximum and minimum values in the domain of the function.

Answers, problem 1

The function increases without bound as x gets large, and decreases without bound as x gets small, so there are no absolute maximum or minimum values.

We can find the local maximum and minimum by finding f′(x) and equating it to 0

Therefore f′(x) = 0 = (3x² - 6x - 4)/10

There is a local minimum value of −1.313 at

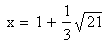
and a local maximum value of 0.113 at

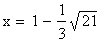
Next ≈ Up