Case Study: Population Modeling: Quiz

Problem 5

The growth of some populations is modeled by a pattern of numbers called the Fibonacci numbers. Consider a population of blue bunnies that begins with one pair of adults. Suppose that each pair of adults produces a pair (one male, one female) each 6 months. The immature pair grows to maturity in 6 months, joining the adult population in producing a new pair every 6 months thereafter.

The number of adult pairs counted each 6 months follows the sequence 1, 1, 2, 3, 5, 8, 13, ... . This is the Fibonacci sequence.

  1. How does the number of immature pairs relate to the number of adult pairs?
  2. How many adult pairs will there be at the end of 6 years?
  3. Graph the Fibonacci sequence, and the best-fitting exponential using the first 10 numbers in the sequence. How well does the exponential model the Fibonacci sequence?

Answers, problem 5

  1. Each adult pair produces an immature pair, so the immature pairs lag the adults by 6 months. The number of immature pairs is therefore 0, 1, 1, 2, 3, 5, 8, ... .
  2. 144

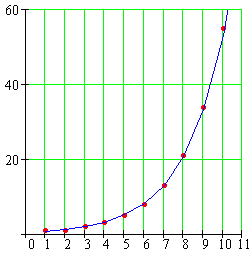
  3. The exponential fits the Fibonacci sequence very well.

Previous ≈ Up