Solutions for Homework sheet 5¶
a. Create a numpy array of length 5 with all elements set to 0.
import numpy as np
A=np.zeros(5)
print A
b. Create a 2 dimensional numpy array of length 4 × 4 with all elements set to 1.
A=np.ones((4,4))
print A
c1. Create a 2 dimensional numpy array of length 5 × 5 with all elements set to 10.
A=np.full((5,5),10)
print A
c2. Create two different numpy arrays with elements [1, 3, 8] and with elements from 1 to 100 divided into 10 evenly spaced numbers.
A=np.asarray([1,3,8])
print A
B=np.linspace(1,100,10)
print B
d. Create a 2 dimensional numpy array filled with random values. Find their datatypes.
A=np.random.rand(4,4)
A.dtype
e. Let say we define an array X1 as follows:
X1 = np.eye(2)
Find the dimension and type of array X1.
import numpy as np
X1 = np.eye(2)
print X1.shape
f. Let say we define an array X1 as follows
X1 = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
Print the first row and column of the array X1, also print the last element of 3rd row.
import numpy as np
X1 = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
print X1[0,:]
print X1[:,0]
print X1[2,3]
g. Let say we define an array X1 as follows
import numpy as np
X1 = np. array ([[10 ,12 ,13 ,14] , [5 ,6 ,7 ,8] , [19 ,10 ,11 ,12]])
Obtain a new array X2, which has same elements as X1 except elements smaller than 10 are set equal to 0.
import numpy as np
X1 = np.array ([[10 ,12 ,13 ,14] , [5 ,6 ,7 ,8] , [19 ,10 ,11 ,12]])
X2=X1
X2[X2<10]=0
print X2
h. Define two 2 × 3 numpy arrays a and b. The first row of a has elements [1, 2, 4] and the second row has the elements [4,5,6]. The first row of b has elements [2, 2, 2] and second row has elements [5, 5, 6]. First take the transpose of a and b then carry out an element wise multiplication on them.
a=np.array([[1,2,3],[4,5,6]])
b=np.array([[2,2,2],[5,5,6]])
print a.T*b.T
(ii) Lists¶
a. Define a python list with elements [9,10,11,12] and find out the length of this list.
L=[9,10,11,12]
print len(L)
b. Define a python list with elements [60.1, 50, 80, 10, 12.5] , sort this list in increasing order.
L=[60.1, 50, 80, 10, 12.5]
L.sort()
print L
Define a python list with elements [’Tom’,’John’,’Jack’,’Kate’], remove ’Tom’ from this list and add ’Dan’ to this list. Next write the resulting list in reverse order.
L=['Tom','John','Jack','Kate']
L.pop(0)
print L
L.append('Dan')
print L
d. Define a 3 × 3 matrix in form of a python list, all the elements of the first row should be 1, all the elements of the second row should be 2 and all the elements of the third row should be 3.
M=[[1, 2, 3, 4],[5, 6, 7, 8], [9, 10, 11, 12]]
print M
(iii) Dictionary¶
a. Create a python dictionary with keys ’Name’, ’Course’, and ’Year’ and associated values as ’Nancy’, ’Chem01’ and ’2017’.
b. Print the keys and values of the dictionary created above.
D = {'Name': 'Nancy', 'Course': 'Chem01', 'Year': 2017}
print D.keys()
print D.values()
Control Statements¶
a. Using if statement write a code in python which calculates square root of an integer if it is positive.
x=input('Input a positive integer')
if(x<0):
print 'Negative Integer'
else:
print 'Square root of the given integer=', np.sqrt(x)
b. Using if else statement write a code in python which checks whether a given username and password is correct.
uppair_dict={'Username':'math50','Password':'123xyz'}
User=raw_input('Input username:')
import getpass
Pass=getpass.getpass('Input password:')
if(User==uppair_dict['Username'] and Pass==uppair_dict['Password']):
print 'Congratulations, your username and password are correct'
else:
print 'Username/Password is not correct'
c. Use for loop to produce the following output from python code.
5, 10, 15, 25, Loop finished
for x in range(5,25,5):
print x,',',
print 'Loop finished'
d. Use a for loop to print all the elements from the list [’Jack’,’Jill’,’Jamie’,’John’].
L= ['Jack','Jill','Jamie','John']
for name in L:
print name,
e. Use a for loop to add all the elements from the numpy array [4, 1.9, 3.1, 7, 2.6, 5.3, 3, 4]
L=[4, 1.9, 3.1, 7, 2.6, 5.3, 3, 4]
s=0
for x in L:
s=s+x
print s
f. Use while statement to write a code which produces the following output
Your guess for the given integer : 100 Wrong! Lower than 100.
Your guess for the given integer : 45 Wrong! Higher than 45.
Your guess for the given integer : 50 Correct! you guessed it.
The while loop is over.
Done
running=True
X0=50
while(running):
X=input('Guess the integer')
if(X>X0):
print 'Your guess for the given integer :', X, 'Wrong! Lower than', X
elif(X<X0):
print 'Your guess for the given integer :', X, 'Wrong! Higher than', X
elif(X==X0):
print 'Your guess for the given integer :', X, 'Correct! Higher than', X
running=False
print 'The while loop is over'
print 'Done'
g. Use numpy arrays and for loops to solve the following problem from the course:
Consider a normal error regression model: $Y_i=\beta_0+\beta_1X_i+ \epsilon_i $. Where $\epsilon_i$ are independent and distributed as $N(0,10)$. $\beta_0=0.10$, $\beta_1=2.15$, $i=1,...,5$ and in these $5$ trials $X_i$ takes the values $\{5,10,15,20,25\}$. You are given that for every trial $i$ there are $k$ different observations of $Y_i$. Plot a scatter plot for $k=10$ between $X$ and $Y$.
X0=np.arange(5,30,5)
k=10
Y1=np.zeros(5*k)
X1=np.zeros(5*k)
labels=[];
l=0
for i in range(0,5):
for j in range(0,k):
epsilon_1=np.random.normal(0,1,1)
Y1[l] =0.10+2.15*X0[i]+epsilon_1[0]
X1[l]=X0[i]
l=l+1
import matplotlib.pylab as plt
%matplotlib inline
plt.figure(figsize=(15,7))
plt.subplot(1,2,1)
plt.scatter(X1,Y1,c='r',s=80)
plt.xlabel(r'$X$',fontsize=25)
plt.ylabel(r'$Y$',fontsize=25)
plt.xlim(3,28);
plt.ylim(4,60)
3. Basic Statistics¶
(i) Let random variable $X$ assumes outcomes $x_1,.....,x_n$. If the probability of outcomes is given by the probability function ${f(x_i)= P(X=x_i)}$ then what will be the expected value of $X$ i.e., $E\{X\}$? What will be the variance $\sigma^2\{ X\}$? If $a$ and $c$ are constants then what will be $E\{a+cX\}$ and $\sigma^2\{a+cX\}$?
(ii) The 90th percentile of a normal distribution is how many standard deviations above the mean?
import scipy.stats as st
format(st.norm.ppf(0.9),'.4f')
The 90th percentile is 1.28 standard deviations above the mean.
(iii) State the properties of independent and identically distributed (i.i.d.) random variables.
Independent identically distributed random variables are mutually independent (any given pair of variables has a covariance of zero and a coefficient of correlation of zero), randomly selected, and each have the same probability distribution function.
(iv) Write down the expression for the probability density function (pdf) of a normal random variable X.
The density function for a normal random varaible X
$$f(X)=\frac{1}{\sigma\sqrt{2\pi}}\exp\bigg[ \frac{1}{2} \bigg( \frac{X-\mu}{\sigma} \bigg)^2 \bigg] $$for $$- \infty < X< \infty$$
Where $\mu$ is the mean and $\sigma^2$ is the variance
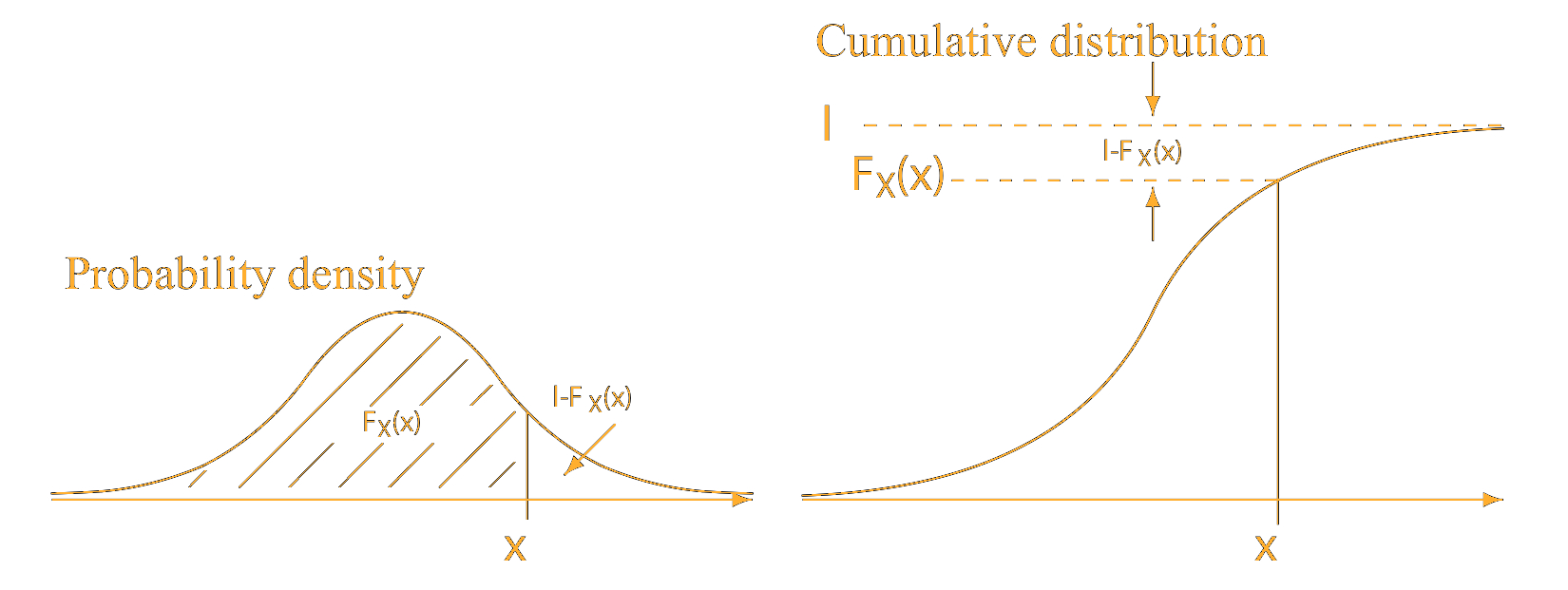
(v) Explain cumulative distribution function (cdf) with the help of a mathematical expression and sketch.
- The cumulative distribution function (cdf) of a discrete random variable $X$ is defined as:
- The cumulative distribution function (cdf) $F(x)$ for a continuous random variable $X$ with probability density function $f$ is defined by:
for $- \infty < x< \infty$.