WHAT ACHILLES SHOULD HAVE SAID TO
THE TORTOISE

BY J. F. T HOMSON

IN 1895 Lewis Carroll published in Mind¹ [New Series, vol. IV, pp. 278-80.] a brief dialogue, `What the Tortoise said to Achilles'. The intention of the story is, plainly enough, to raise a difficulty about the idea of valid arguments, a difficulty similar, or so Carroll implies, to Zeno's difficulty about getting to the end of a race-course. Different writers have said different things, usually briefly, about what the difficulty is. Let us first consider just what happens in the story and then try to see what problems it raises.

The topic of the story is a certain task set to Achilles. The Tortoise says that there might be someone who accepted the two propositions:

(A) Things that are equal to the same are equal to each other, and

(B) The two sides of this triangle are things that are equal to the same,

but did not accept

(C) If things that are equal to the same are equal to each other, and if the two sides of this triangle are equal to the same, then the two sides of this triangle are equal to each other.

Such a person, he says, would not as yet (Lewis Carroll's italics) be under any logical necessity to accept the consequent of C, namely

(Z) The two sides of this triangle are equal to each other.

He asks Achilles to pretend that he is such a person and to force him, `logically', to accept Z. Since it is Achilles' failure to do this which is the point of the story, we must ask how his failure comes about.

Achilles sets about his task in an unexpected way. You might expect him to begin by trying to find out why the Tortoise does not accept C. Instead, he asks him to accept C, i.e. asks him to accept that very proposition which he has just said he does not accept. You might now expect the Tortoise to laugh, or to be surprised, or at least to say: `But I don't accept C, or so we are pretending.' Instead he grants the request, or says he does, and for no other reason than that he has been asked to. He is now on record as having accepted A, B, and C. And now, Achilles says, he must accept Z. `If you accept A and B and C, you must accept Z . . . because it follows

logically from them.' The Tortoise replies in effect that just as the might be someone who did not accept the hypothetical C which connects A and B with Z so there might be someone who did not accept the hypothetical, call it D, which connects A and B and C with Z, and that such a person might accept each of A and B and C and still not accept Z. When Achilles asks him to accept D he does so, just as he accepted C, and the story goes on as before. Apparently the end of this `ideal race-course' is never to be reached.

To see clearly what is happening, let us relabel the propositions involved. The original premises A and B we can collapse into one conjunctive premise C₀. The first hypothetical C we shall sometimes call `C<sub>1</sub>', the second, D, `C₂', and so on. The hypothetical with antecedent X and consequent Y we shall call `X Y'. Then the sequence of propositions successively accepted by the Tortoise is

 
C0 = (A & B)
C1 = C0 --> Z
C2 = (C0 & C1 --> Z
C3 = (C0 & C1 & C2) --> Z

etc. The sequence is generated by the rule that the first term is (A & B) and each term thereafter is the hypothetical whose antecedent is the conjunction of the preceding terms and whose consequent is Z. The behaviour of the Tortoise also follows a simple inductive rule. He accepts the first term of the sequence. At each stage thereafter, having accepted C₀, C₁, . . ., C_n, he refuses to accept Z on the grounds that he has not yet accepted C_n+1, is asked to accept this one, does so, and the game goes on as before.

It is plain that as long as this procedure is adopted he will never be brought to accept Z. If at every stage Z is not to be accepted until some other proposition is accepted, Z will never be accepted. But the sensible reader will ask: `So what?' Why should this procedure be adopted in the first place? How does, why should, an infinite sequence of hypotheticals C₁, C₂, . . . get into the picture?

The Tortoise represents himself as someone who accepts A and B but not C and he says that, being in this position, he is not as yet under any logical necessity to accept Z. This is wrong. Whether or not he accepts C, it is logically true. That means that the argument from A and B to Z is logically valid and that the Tortoise in accepting A and B commits himself to accepting Z. So he is already under a logical necessity to accept it. To say that he is not (`as yet') is precisely to deny that the argument `A, B, 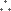Z' is logically valid. But if that were true there would be no problem; we should not expect Achilles to be able logically to force the Tortoise to accept Z on the basis of an invalid argument. It may be objected that the Tortoise is justified `from his own point of view' in saying that he can accept A and B without accepting Z. The reply is that this point of view is a mistaken one and Achilles' task is precisely to make him give it up. How can he do that? He must first find out why the Tortoise does not accept C. Someone who was really unwilling or unable to grant the truth of this proposition would either have some reason, perverse or ingenious or both, for thinking it false or doubtful, or he would not have considered sufficiently carefully just what proposition it is. Perhaps there are other possibilities. But anyway Achilles must ask the Tortoise to show at least part of his hand. If the latter's pretence not to see that C is true is to be considered at all it must be taken seriously.

What Achilles does in the story is quite different. In effect he says: So you don't accept C. Well then, will you accept C?' To make such a request in such circumstances is ridiculous, and to accede to it is ridiculous too. Achilles makes it because, as he himself says, if you accept A and B and C you must accept Z -- `it follows logically from them'. But this is a bad reason. In saying that Z follows from A and B and C Achilles implies that it does not follow from A and B alone, he implies that these premises are not by themselves sufficient. He thus accepts the implications of the `not as yet' and so makes a nonsense of his acceptance of the idea that he should (`logically') force the Tortoise to accept Z. And anyway in so far as the latter is justified, `from his own point of view', in not accepting Z, he would be justified also in refusing to accept C. He could say: `Of course if I accept C I shall then have to accept Z, but that is not in question. You are trying to get me to accept Z. You can do that by presenting me with an argument which I see to be valid and which has premises which I am able to accept. I don't accept that the argument "A, B, 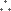Z" is valid. So, as you should have foreseen, I can't accept C. So I can't accept all the premises of your second argument, "A, B, C, 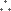Z". From the point of view of establishing its conclusion, a valid argument with false premises is no better off than an invalid one. In your case the falsity of the false premise in the second argument follows directly from the invalidity of the first. So not only does the second argument give me no more reason to accept Z than the first one did, but there is just the same lack of reason in each case.'

Given an argument with premises P₁, P₂, . . ., P_k and conclusion Q let us call (P₁ & P₂ & . . . & P_k) Q the hypothetical associated with that argument, and let us call the argument with the same conclusion and premises P₁, P₂, . . ., P_r, (P₁ & . . . & P_k) Q the strengthened form of the original argument and a strengthened argument. An argument may fail to establish its conclusion on either or both of two counts; it may have one or more false premises, and, independently, the relation required to hold between the premises and the conclusion may not hold. It is clear that a strengthened argument will always be valid and so will never fail on the second count, and that if an argument fails on any count its strengthening must fail on the first of them. In particular, if an argument fails by not having enough premises its strengthening will escape that weakness but must, just because it is the strengthened form of that argument, fail by having an unacceptable premise. It follows that from the point of view of getting arguments which establish their conclusions the operation of strengthening is either redundant or futile.

We need not be inhibited from accepting this by feelings of loyalty to the old idea that some arguments have suppressed premises. Certainly, if the argument `P, 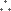Q' can have a suppressed premise, why should it not have the suppressed premise P Q? About the idea that arguments do have suppressed premises, a good deal needs to be said, but it does not need to be said here. For arguments which are said to have suppressed premises are said to be valid in virtue of having them, and valid arguments do not need to be strengthened. In other words, if we wish to say that an argument has suppressed premises we must take this seriously and really count the suppressed premises among its premises. (The observation that strengthening is either redundant or futile is quite independent of the question whether `valid' must always mean `logically valid' or whether logically valid arguments are just a sub-class of valid arguments.)

All this, then, or part of it, is what the Tortoise could have said in reply to Achilles' request that he accept C. Instead, he accedes to the request and still does not accept Z. But is this inability the old inability in a new guise or is it a new one? Whether Lewis Carroll realized the fact or not, it is a new one. The failure to see the truth of C is, roughly speaking, a failure to appreciate the transitivity of the relation sameness of length. The failure to see that C₂ is true is a failure to appreciate the logical force of if. If there could be someone who thought that C₁ was false or doubtful, he might well be, and probably would be, someone who at once saw the truth of C₂. So at this second stage of the game the Tortoise has changed his ground. He began by representing himself as someone who could not accept a certain hypothetical. He now pretends to have accepted that hypothetical and represents himself as someone who does not see the truth of a quite different hypothetical. (And in a moment he will change his ground yet again; he will pretend to accept C₂ and will make difficulties over C₃. But these later subterfuges are not very interesting.)

We now see how the infinite sequence of hypotheticals gets into the story. When he says that someone who accepts A and B but not C is not as yet under any necessity to accept Z, the Tortoise implies not only that the premises A and B are not sufficient but also that A and B and C would be, and also that he sees that this is so. When having accepted C he shifts his difficulty to C₂ he implies that if only he were able to accept that one he would be able to accept Z. So at each stage he introduces a new hypothetical into the discussion and tempts Achilles to ask him to accept it. The sequence of hypotheticals introduced in this way is infinite because however many premises he accepts he pretends not to see that there are enough.

We have also answered the question why Achilles fails in his task. His first mistake is in asking the Tortoise to accept C. By doing this he implies that he is not after all in any position to force him, logically, to accept Z. But if we think that his failure is a punishment for that mistake, we must be clear that the punishment does not fit the crime. For the Tortoise ought not to have acceded to the request and having acceded to it he ought to have accepted Z. So the second thing to be clear about is that the Tortoise cheats. Instead of presenting Achilles with just one problem he presents him with infinitely many; though this is concealed by the fact that Achilles does not really try to solve any of them.

The extreme eccentricity of the behaviour of both of the characters may well make us wonder whether Lewis Carroll knew what he was up to in writing the story. Certainly it cannot be merely taken for granted that he intended to advance some moderately clear thesis or theses about inference but chose to do so in a veiled and cryptic way. It is just as likely that the story is the expression of a perplexity by someone who was not able to make clear to himself just why he was perplexed. But we may still ask what points of logical interest emerge from it. I shall mention just two.

We say that if a triangle is isosceles the angles at the base must be equal, that if Tom is older than Dick and Dick older than Harry then Tom must be older than Harry. More generally we say that if such-and-such it must be the case that so-and-so. This use of `must' is a signal that something is being claimed to follow from something else. But we also say: if you accept that such-and-such then you must accept that so-and-so. This use of `must' can be misunderstood. `I accept A and B and C and D', says the Tortoise at one point. `Suppose I still refuse to accept Z?' `Then Logic would take you by the throat and force you to do it', Achilles replies. But Logic does no such thing.

`If you accept the premises of a logically valid argument, you must accept its conclusion.' Well, why must he? ó This statement does not mean that if someone does accept the premises of such an argument he will accept its conclusion, let alone that he will necessarily accept it. He may accept the premises without knowing or without noticing that they are the premises of a logically valid argument with that conclusion. Even when the argument is put before him he may be unable to understand it or unwilling to try. Or he may not see that it is valid, or may think that it contains such-and-such a fallacy. He may even say: `Since the premises are true and the conclusion false the argument must be fallacious, though I can't for the moment see where the fallacy is.' Even when he has seen and examined the argument and convinced himself that it is valid he may still not accept the conclusion, since he may prefer to retract his acceptance of the premises. What is true is that in accepting the premises he commits himself to acceptance of the conclusion. Why? Because what we are here calling the conclusion is something that follows from premises which he accepts. But why then does acceptance of a set of premises commit one to acceptance of their consequences? This question can be regarded only as a request for an explanation of the notion of a consequence and of a logically valid argument or as an occasion to remind someone of what these notions are. Part of this explanation is that the set consisting of the premises of a logically valid argument and the negation of its conclusion is logically self-inconsistent and so must contain at least one falsehood. So anyone who accepts the premises and denies the conclusion has committed himself to at least one falsehood. This is the threat behind the `must'. `If you assert the premises and deny the conclusion, you will have said at least one false thing, however the facts may turn out to be.'

`If you accept these propositions you must accept that one' -- this is characteristically said by someone who is trying to get his hearer to accept something. So it is said by someone who is or has been arguing. Then we may suppose that an argument has been put forward and that the hearer is or has been or soon will be examining it. But when the speaker says what he says he is only saying that the argument is valid. It follows that although this remark is typically made by someone who is arguing it is not itself a piece of an argument. It is one thing to put forward an argument, even a valid one, and another to say that you are arguing validly. It is one thing to propose for acceptance propositions which (you hope or believe or know) entail another proposition and another thing to say that they do. In arguing, you may need to point out that you are. You then (as it were) step aside from what you are doing and comment on your own performance. But then the performance must be there, independently of the comment, to be commented on.

The proposition that such-and-such an argument is valid can itself be a premise of an argument². [For example, an argument designed to show that such-and-such a book contains exactly one valid argument.] But it cannot be a premise in the argument to which it refers. If you want to say of some argument that it is valid you must be able to say what argument it is that you want to make this claim for. The argument must be identifiable. And the identification must be such as to allow the claim that it is logically valid to be assessed. To assess that claim we need to know what the premises are and what the conclusion is. So the premises must be identifiable independently of the claim that there are enough of them.

What has just been said about the statement that the argument `P₁, ..., P_k, 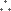Q' is logically valid must hold also of the statement that if P₁ and P₂ and ... and P_k then necessarily Q. For the latter statement is logically equivalent to the former. It does not matter that the former argument is explicitly about an argument and the latter not. Just as the statement that an argument is logically valid cannot turn out to be a premise in that argument, so, and indeed very obviously, a hypothetical cannot turn out to be its own antecedent or a conjunct in its own antecedent. So if, having got you to accept premises P₁ to P_k and wanting you now to do what I think you are committed to doing, viz. accept Q, I assert that if P₁ and ... and P_k then necessarily Q, I am not, or should not regard myself as, asking you to accept another premise. For ex hypothesi I suppose that you already have enough premises.

To say this is not to deny that some arguments have hypotheticals as premises and have them as premises in just the way they have other premises³. [At least one writer on the story has been led to deny this. See D.G. Brown, `What the Tortoise taught us', Mind, vol. LXIII (1954), p. 179.] Someone who, having put forward some premises, puts forward a hypothetical having the conjunction of those premises as its antecedent may very well intend the hypothetical to be counted as another premise. If what is in question is the validity of your argument, it is up to you to say what its premises are. You may list as the set of premises enough to make it logically valid, and you may, either knowingly or unwittingly, list some that are redundant. All that is being said is that if you list your premises and all of your premises and then assert what we called the hypothetical associated with the argument whose premises these are, that hypothetical just cannot turn out to be one of the premises already listed. This rests on the fact that a hypothetical cannot be a conjunct in its own antecedent, and this rests in turn on the fact that no sentence which expresses proposition can be longer than it is. It is therefore very obvious. [BAD TEXT] it is enough to clear up one of the misunderstandings in the story. When Achilles said that if you accept A and B and C you must accept Z he was claiming that the argument that since A, B, and C, therefore Z was logically valid, had enough premises, and so was not, or should not have regarded himself as, offering another premise.

So the first point of interest is that we must distinguish between arguing and talking about an argument, between giving reasons, even good ones, and saying that some reasons are good ones. In particular, if someone in arguing asserts a hypothetical and makes it clear, by using some such signal-word as `must' or `logically' or `necessarily', that he regards it as necessarily true, he may be offering a premise and he may be doing something equivalent to commenting on a set of premises already identifiable. What he cannot be doing is both at once.

The second point is connected with the first. Before we can hope to understand what is going on between Achilles and the Tortoise we must be clear that to assert the truth (logical truth, or acceptability, or reasonableness, etc.) of a hypothetical is equivalent to asserting the validity (logical validity, or cogency, etc.) of the argument with which that hypothetical is associated. It follows that to accept the hypothetical is to commit oneself to accepting the validity of the argument. But what is it to accept the validity of an argument? One thing that shows that you accept it is that if you assert the premises you are willing to go on and say `therefore' and then assert the conclusion. But then suppose that someone claims to accept the hypothetical and to accept the premise but is not willing to assert the conclusion? How can we get him actually to do what he is committed to doing, i.e. accept Q? It is natural to think of pointing out to him that Q follows logically from P and P Q, and this thought may then seem suspect for something like the following reason: we began by wanting him to accept the argument `P, 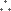Q' and now seem to be trying to get him to accept the (different) argument `P, P Q 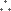Q'; what if he will not accept this one either, shall we then have to start again? The suspicion is dispelled when we reflect that the latter argument really is different from the former one, so that someone might accept it and not accept the former. We must also remember that when we claim validity for the latter argument we are not, or at least should not regard ourselves as, arguing that since it is valid so is the original one. Such an argument would be fallacious. Strengthened arguments are always valid. So the second point of interest is that logically valid arguments are of different kinds. Consider for example the three arguments `A, B, 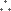Z', `A, B, C, 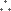Z' and `B, 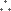Z'. The first is formalizable in first-order predicate logic with identity. The second is formalizable in truth-functional logic and in any one of a large number of weaker systems of propositional logic. The third, though logically valid, is not formally valid at all.

We naturally feel a reluctance to admit that someone could accept A, B and C and not accept Z. Behind this is the fact that if someone claims to accept the premises of a very simple argument and does not accept the conclusion it is sometimes reasonable to suppose that he has not really accepted the premises⁴. [See the paper cited in the previous footnote.] That is, we sometimes make it a necessary condition for someone's having accepted a set of propositions that he accepts such-and-such consequences of them. No general rules can be given for when this is reasonable, but it is probably a mere prejudice to think that the difficulty arises especially over `A, B, C, 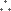Z' and does not arise at all over `A, B, 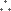Z'. But the important point is that it is not the Tortoise's refusal to accept Z at the second stage that shows that Achilles was silly to offer him C as a premise at the first stage; even though Achilles was silly to do so, for reasons we have seen. What that refusal shows is rather something about the Tortoise.

In conclusion I should like to comment briefly on some remarks about the story in Professor G. Ryle's paper If, So, and Because.⁵ [In `Philosophical Analysis' edited by Max Black, New York, 1950.] Ryle is here considering the question: How does the validity of the argument `P, 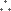Q' require the truth of the hypothetical P Q? He discusses among others the following answer: `The argument is always invalid unless the premise from which Q is drawn incorporates not only P but also P Q. Q follows neither from P Q by itself, nor from P by itself, but only from the conjunction P and (P Q).' Ryle comments on this idea as follows: `But this notoriously will not do. For, suppose it did. Then a critic might ask to be satisfied that Q was legitimately drawn from P and (P Q); and to be satisfied he would have to be assured that if P and also if P and Q then Q. So this new hypothetical would have to be incorporated as a third component of a conjunctive premise, and so on for ever ó as the Tortoise proved to Achilles. The principle of an inference cannot be one of its premises or part of its premise. Conclusions are drawn from premises in accordance with principles, not from premises which embody those principles.'

It seems that what Ryle calls the principle of an inference is either what we have called the hypothetical associated with the argument or some statement or formula of which that hypothetical is an exemplification or a general proposition of which the hypothetical in a particular case. In each of these cases his statement that the principle cannot be one of the premises or part of its premise is clearly correct. It is hardly necessary to repeat the argument: the `principle' of the argument `A, B, 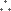Z' is, roughly speaking, the principle that a certain relation is transitive; if we strengthen that argument by adding the appropriate hypothetical as a redundant premise the new argument has a quite different principle. But, more or less clearly implicit in what Ryle says, there is the suggestion that Achilles fails in his task because he does not distinguish premises from principles, and, coupled with it, the idea that the necessity for this distinction can be demonstrated by means of a regress-argument. This does not seem correct.

We must notice first that the suggestion which Ryle is attacking is much more seriously confused than his comment on it brings out. For how in it are the letters `P' and 'Q' being used? If they are constants we can hardly be expected to assess the idea that the argument 'P, 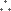Q' is not as it stands valid, since we have not been told what propositions P and Q are. But if they are variables, the suggestion comes to this: no argument is valid, but, given an argument, which will of course be invalid, we can always obtain from it an argument (its strengthened form) which will be valid. And while it is absurd to hold that no arguments are valid, it is doubly absurd to hold this and then say that some arguments can be made valid. If for no values of 'P' and 'Q' does P yield Q, then, in particular, P & (P Q) does not yield Q, since P & (P Q) is just one value of `P'.

So, to dismiss the suggestion, we need only be clear what it comes to, and we do not need to invoke a regress-argument. But it is not clear either that we are entitled to do so. The suggestion that we are depends upon thinking that if someone cavils at the argument 'A, B, 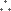Z' on the grounds that C is not one of its premises he is somehow committed to cavilling at 'A, B, C, Z' because C₂ is not one of its premises. But this is just wrong. If someone had a pre-judice in favour of truth-functionally valid arguments he would be consistent in rejecting the first argument as invalid and then accepting the second. A critic who then asked to be satisfied that Z was legitimately drawn from A, B, and C would be shown a truth-table and that would be that. So there is no force in Ryle's suggestion that `this new hypothetical (here, C₂) would have to be incorporated as a third component of a conjunctive premise'.

If all this is correct, then what is most usually taken to be established by the story, namely that we must not try to make the `principle' of an inference one of its premises, on pain of running into an infinite regress, is wrong, and is not established by the story. What people who say this mean by taking the principle as one of the premises turns out to be what we called strengthening, and strengthening does not run us into a regress. The mistake of supposing that it does comes partly from failing to notice that the Tortoise changes his ground, shifts his difficulty, at the second stage. It is true that if someone thinks that every argument needs to be strengthened he will think or be committed to thinking that every argument is invalid, but to expose this we do not need to invoke a regress argument anyway. Neither does any such argument help us in seeing what needs to be seen, the way in which strengthening is either redundant or futile. The infinite regress is just an infinitely long red herring.