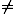INFINITY IN THEOLOGY AND MATHEMATICS

Can we apply the same concepts to both the finite and the infinite? Is there something distinctive about the infinite that prevents attribution to it of concepts that we can attribute to the finite? If so, then this could be a reason for our difficulties in talking about God — God is infinite, and our concepts, applying, as they do, to the finite objects of our experience, cannot be `extended' to the infinite. God's infinity is sometimes used as an explanation of theological difficulties like the problem of evil or the paradoxes of omnipotence: we do not really know what we mean when we attribute infinite goodness or power to God.

The mathematical concept of the infinite may be able to shed some light on the theological concept. In mathematics, there is a clearly developed concept of the infinite. We might expect that if there are problems of expressibility related to infinity, they will appear in mathematics as well as in theology. Since the mathematical concept is clearer, the source of any difficulties with it may be clearer as well.

I shall suggest the following conclusions. First, the difficulty that we shall see in pinning down the meaning of `infinite' in its application to God is partly the result of there being two disparate trends in theology: one that tries to find an answer to the problems that come from God's infinity, and one that insists on the impenetrable mystery of the infinite. Second, the development of the mathematical concept of the infinite can shed light on the theological concept not so much by indicating the possibility of a parallel development and clarification of God's infinity; but rather by showing that the attribution of infinity to God may well be — at the present stage of development of the mathematical concept — more figurative than literal. The concepts of the mathematical infinite and the theological infinite may at one time have been quite close; but by now there is at most a metaphorical connexion. And third, infinity is less a cause or a reason for inexpressibility than an attribution resulting from the experience of God as in some degree mysterious.

1. HISTORICAL SURVEY OF THE INFINITE

The following general classifications of infinity are to be developed and refined through a brief historical survey: first, the potential infinite; second, the actual infinite; and third, the theological infinite.

Even in mathematics, there is not a simple dichotomy between the finite and the infinite. Opposed to the finite are the potential infinite and the actual infinite. The potential infinite is an extension of the finite, constructible from the finite by some rule or process that is never in fact completed. The actual infinite, on the other hand, is conceived as an actually existing collection of an infinite number of parts. The actual infinite could be regarded as the completion of a process that builds the infinite from the finite. This is the actual infinite of set theory.

God's infinity, however, is not conceived as one of these species of mathematical infinity. Descartes and Leibniz, for example, make a further distinction between the mathematical infinite and what they call the absolute infinite (and which I shall call the theological infinite). The conception of the theological infinite is not a conception of an infinite collection, but rather of the unbounded or unlimited.

1.1 The mathematical infinite

Aristotle distinguished between the potential infinite and the actual infinite. In none of the experiential sources for the concept of the infinite does the infinite actually exist. It exists only potentially, by addition or division. Aristotle argues that saying that the infinite potentially-is, is not like saying that a statute potentially-is. If a statute potentially-is, that means that there will be an actual statute. The infinite does not potentially exist in this sense — there will be no actual infinite. Rather, to say `there is the infinite', according to Aristotle, means that one thing after another will be coming into being. The infinite takes place in a succession of different finite things: by the division of the parts in magnitude; or by addition in the succession of moments or beings. The infinite has being only as a process that can be repeated over and over again without end, but which, at any moment, has only a finite number of components.¹ [Aristotle, Physica, translated by R.P. Hardie and R.K. Gaye, in The Basic Works of Aristotle, edited by Richard McKeon (N.Y.: Random House, 1941), 206a. ]

Aristotle's idea that the infinite has being only potentially and not actually was denied by Cantor. In Cantor's view, a set has to be regarded as a whole, as a totality with all the parts simultaneous. This appears to obviate the distinction between the potential and the actual infinite.

Cantor's actual infinite may not be the same as Aristotle's actual infinite, even though Cantor represents it as such. As Bochner points out,² [Salomon Bochner, `Infinity', in Dictionary of the History of Ideas, vol. 11 (N.Y.: Charles Scribner's Sons, 1973), p. 612.] Aristotle was not talking about number, but about body — physics rather than mathematics. On the other hand, Cantor's actual infinite is in principle constructible by means of a rule or process. Whereas for Aristotle the infinite has being only as this infinitely repeatable rule or process, Cantor's actual infinite could be seen as the completion of such a process. This is not to suggest that the actual infinite is defined by any unique process of construction, but rather that the actual infinite can be seen as what would result from the endless repetition of a process. In any case, this process requires a `subjunctive leap': the actual infinite is not in fact the result of repeating the process an infinite number of times, but rather represents what would result from infinite repetitions. (Similarly, the mathematical statement of Zeno's paradox converges to 1, but determining this limit does not require actually adding up the infinite sum; the limit tells you what result you would get if you had added up the infinite sum.)

Cantor claims that a distinction still remains between kinds of infinite: there are consistent multiplicities, which are infinite sets like the sets of integers; and there are inconsistent multiplicities. These are the infinite sets that in one way or another cause a problem. As he says,

a multiplicity can be such that the assumption that all its elements `are together' leads to a contradiction, so that it is impossible to conceive of the multiplicity as a unity, as `one finished thing' ... the `totality of everything thinkable', for example, is such a multiplicity; later still other examples will turn up.<sup>3</sup> [George Cantor, `Letter to Dedekind', in From Frege to Godel: A Source Book in Mathematical Logic, ed. Jean van Heijenoort (Cambridge, Mass. and London: Harvard University Press, 1967), p. 114.]

It does not seem likely, however, that Cantor's inconsistent sets point to another species of infinity, or to a problem about infinity as such. Cantor's paradox and its cognates do not rely at all upon the size of their domain — they can be stated as well for finite sets. In other words, although there can be inconsistent infinite sets, there can also be finite sets that are inconsistent for the same reason.

1.2 The theological infinite

The actual infinite, as I have said, can be conceived as collection of an infinite number of parts, the completion of some process that builds the infinite from the finite. The only problem with actually infinite sets, if there is a problem with them, is that there is not enough time to build them. Nevertheless, they are still the kinds of things that could be built from a collection of parts. The theological infinite, however, is not conceived as an infinite collection, but rather as the unbounded or unlimited; it is not in any sense constructible from the finite because it is not a collection at all, not an extension of the finite.

Descartes puts this as a distinction between the infinite and the indefinite, between a positive and a negative idea. The actual or potential infinite of mathematics is more properly called indefinite; only God is infinite. Indefinite things are those in which we observe no limits, and perhaps can conceive no limits; but we cannot prove that they must have no limits. What we can call infinite, on the other hand, is that in which we not only observe no limits, but also can be certain that there can be no limits.⁴ [Descartes, Principles of Philosophy, in The Philosophical Works of Descartes, 1, trans. Elizabeth S. Haldane and G.R.T. Ross (Cambridge: Cambridge University Press, 1931), 1, xxvii.]

God is the only thing I positively conceive as infinite. As to other things like the extension of the world and the number of parts into which matter is divisible, I confess I do not know whether they are absolutely infinite; I merely know that I can see no end to them. . . .⁵ [Descartes, letter to More, 5 February 1649, in Philosophical Letters, trans., ed. Anthony Kenny (Minneapolis: University of Minnesota Press, 1981), p. 242.]

We have a positive understanding that God is without limits, but

in regard to other things ... we do not in the same way positively understand them to be in every part unlimited, but merely admit that their limits, if they exist, cannot be discovered by us.⁶ [Descartes, Principles of Philosophy, 1, xxvii.]

So Descartes says that there are things other than God that are apparently without limits; but he separates the unlimitedness of these other things from the unlimitedness of God by saying that only in the case of God are we certain that there can be no limits. In all other cases, according to Descartes, we can say only that we know of no limits; but there may or may not still be limits.

The idea of the theological infinite is, for Descartes, a different idea from that of the mathematical potential or actual infinite. There is no way that the idea of the infinite can be derived from the indefinite — the idea of the infinite is a positive idea that cannot be constructed from the negative idea of the indefinite. This distinction between the indefinite and the infinite has a crucial part in Descartes' proof for the existence of God: since the idea of God is the idea of an actually infinite being, and I am at most potentially infinite, I could not be responsible for this idea myself.⁷ [Descartes, Meditations, in Haldane and Ross, pp. 166f.]

This distinction of the infinite from the merely indefinite may be apt for some objects — we cannot at present prove, for instance, that there are or that there are not ultimate constituents that would limit divisibility of matter. But what about number? We do seem to be able to prove that number is infinite, in virtue of the fact, for example, that the series of positive integers can be put into a one-one correspondence with a proper subset of itself. This is a positive proof of infinity, of the sort that Descartes would reserve only for God. In separating God's infinity from the merely indefinite of mathematics, Descartes perhaps means to retain God's infinity as something absolutely unique, mysterious and strange, in the face of which we stand in awe. But Descartes' definitions of the infinite and the indefinite do not provide as much support for this strangeness as Descartes intended.

Leibniz, like Descartes, makes God's infinity something other than another species of mathematical infinity. In a sense our idea of the infinite is for Leibniz derived from the finite and from the impossibility that we should ever come to the end of our ability to continue adding or dividing. But our ability thus to build the infinite from the finite, to understand that we can keep applying the same rules or processes over and over, getting a new result each time, is grounded in the idea of the theological infinite. The idea of the theological infinite, which grounds the mathematical infinite, is an idea of an attribute of God. (That is, God is infinite; and God's other qualities are in God in the manner proper to an infinite being. Qualities are determined and limited by the nature of the being in which they inhere; in an infinite being, there is no limitation of the quality by the nature of the being.⁸ [This explication of God's infinity is close to Aquinas's: cf. Summa Theologica 17.] ) This absolute infinite `precedes all composition and is not formed by the addition of parts'. It is not, that is, a completed whole, but rather, `an attribute with no limits'.⁹[Leibniz, New Essays on Human Understanding, trans. Peter Remnant and Jonathan Bennett (Cambridge: Cambridge University Press, 1981), 157ff.]

II. POSSIBLE DEFINITIONS OF THE UNLIMITED

The theological infinite, then, is distinguished from the mathematical infinite in that the theological infinite is defined only by the lack of limits or bounds. This could define the mathematical infinite in only the most naive way — we could say, for instance, that there is no end to number. We have to consider what a limit is, in this sense, and what it means to say that something has or does not have limits. Mathematics shows that the infinite cannot be simply identified with the unlimited: there can be a space that is unlimited but finite; and the real numbers between 0 and 1 are an example of the limited but infinite.

It seems that the idea of the unlimited incorporates these factors: the idea that goodness, power and other qualities are not limited by the nature of God as they are limited by the nature of the other beings in which they are found; the idea that the quality is inexhaustible in God; and the idea that God is a sort of `upper bound' of the quality. But none of these conclusively defines `unlimited' on its own; nor do they add up to a conclusive definition.

2.1 Completeness

In his historical survey of the concept of the infinite, S. Bochner has suggested that the theological infinite is a qualitative, rather than a quantitative, infinite. The idea of a qualitative infinite is not at all clear, however. The qualitatively infinite might be seen as something that `expresses a degree of completeness or perfection of something structurable'.<sup>10</sup> [Bochner, `Infinity', p. 614.] According to Aristotle, completeness rules out infinity altogether: what is complete has nothing lacking to it, and thus nothing outside of it; but the infinite always has something outside it — `outside' in the sense that, since the infinite is an unending process, there is always something that this process has not yet incorporated: another unit to be added or another division to be made.¹¹ [Aristotle, Physica, 206b-207a.] Bochner points out that mathematizations of completeness show that completeness need not rule out infinity; but to say that completeness need not rule out infinity is obviously not to say that infinity can be defined in terms of completeness. It might be suggested that in the qualitatively infinite the quality is infinitely present. This does not, however, seem to add anything to the idea of the unlimited. To say that in God being, goodness, power and so forth are infinitely present is to say no more than that the quality is not limited by the nature of God, as it is limited by the nature of any creature in which it is found.

2.2 Inexhaustibility

The notion of inexhaustibility, of not being able ever to come to the end, is also relevant here. For instance, you could never come to the end of God's infinite mercy: you could never sin to much or too often to be forgiven. Inexhaustibility cannot define the mathematical infinite — something could be practically or virtually inexhaustible, and yet be (hugely) finite. The class of the first 10¹⁰⁰ positive integers is inexhaustibly large in the sense that you could never come to the end of counting them; but it is not infinite. On the other hand, we have seen that the mathematical and the theological conceptions of the infinite are not the same. So the fact that inexhaustibility does not define the mathematical infinite is not conclusive evidence against its defining the theological infinite.

2.3 Maximality and purity

We might try defining theological infinity as maximality — so that saying that God is infinitely good, for instance, means that God is more good than anything else possible. This `upper bound' conception of God's infinity is close to the definition of God as `that than which there can be no greater'. The fact that this definition is relative to a class of possible things, rather than to a class of actual things, means that at least there is nothing contingent or variable about the definition.

This definition of the theological infinite, however, does not fully answer the question of what we mean when we attribute infinity to God. The impact of the infinite on our ability to think about and talk about God is determined by a decision to accept or reject what we might call a `purity postulate'. By `purity' I mean the notion that if God is infinitely good, then there is in God no trace or mixture of evil; if God is powerful, there is in God no trace or mixture of inability; and so forth. We can accept or reject this purity postulate while retaining the definition of God's infinity as maximality. It seems that this postulate of purity is independent of the attribution of infinity to God.

Clearly something could be more good than anything else possible, and still not be purely good, more powerful than anything else possible, and still not purely powerful, and so forth. And in this case, God could still be said to be infinitely powerful — to be more powerful than anything else possible — but still not be powerful enough to eradicate evil altogether. In this case, pure power, pure goodness, would be an impossibility. On the other hand, we might say that this does not capture adequately what we mean to say when we say that God is unlimited. We might want to say that if God's power is infinite, then there cannot be a certain point beyond which it does not extend. If there were, that would be a limit; and hence God's power would be only hugely finite.

The point is that there is no agreement about how far God's lack of limits reaches, no agreement about the acceptance or rejection of this idea of purity. Both Descartes and Leibniz define theological infinity as the lack of limits. But Leibniz does not claim that God can contravene the laws of logic; and Descartes does. For Leibniz, God's power is unlimited in the sense that God can do anything logically possible. For Descartes, God's power is unlimited altogether. Descartes says that God could make a mountain without a valley, or make it the case that 2 + 3 5: that we cannot conceive these things is no indication of a limit to God's power. We need not see a paradox or a contradiction as indicating a limit to God. We can see it, instead, as indicating a limit to our minds.

2.4 Mystery

The idea of God's infinite goodness as the upper bound of possible goodness brings to light one of the sources of the difficulty of defining theological infinity as the lack of limits. In this connexion, it seems that there are always two trends in theology: one that wants to make sense out of God's infinity; and one that wants to preserve God's infinity as an unexplored — and unexplorable — mystery. The definition of `unlimited' and the attitude towards the mystery of the infinite are interwoven. Essentially, the point is that there is no agreement about the extent to which God is unlimited, and hence no agreement on the content of the concept of God's infinite goodness, infinite power and so on.

Can God contravene the laws of logic? Can God do evil so that a greater good will come? We can answer these questions either way, and the meaning of `unlimited' will vary as the answers vary.

Ivan Karamazov wants an explanation of evil that will be understandable for his `finite Euclidean mind': the only answer he gets says that understanding is impossible; and the most he could attain would be an acceptance stemming from mystical love that somehow transcends his own limits. Here is one of the points where the mathematical concept of infinity cannot help us clarify the concept of theological infinity. There are these two trends in theology: one that wants an answer to the problems that seem to come from God's infinity; and one that insists upon the mystery of the infinite. These are not trends that you find in mathematics. And in mathematics a contradiction indicates error: in theology, however, a contradiction can be taken also as indicating that the subject matter lies beyond our grasp.

It seems that the development of the mathematical concept of the infinite has gone on increasingly independently of the theological concept of the infinite. The mathematical infinite has become, particularly during this century, an ordinary, unmysterious operational concept. The theological infinite, however, retains its connexion with mystery. What Bochner calls the "secularization" of infinity has taken place within the realm of the mathematical. In mathematics, there may not be universal agreement about the philosophical meaning of infinity, but there is at least agreement about methods and goals; and there are means of determining, to some extent, the suitability of conceptions of the infinite. In theology, there is no such agreement.

A not uncommon answer to theological difficulties is to say that the difficulties stem from God's infinity: we cannot grasp the infinite, so we cannot answer the questions. But mathematics shows that, while we may not be able to encompass the infinite — we cannot actually pass through all the numbers in an infinite series — we can still grasp the infinite, and by finite means. Mathematical concepts like `addition' can be applied to both finite and infinite collections. Certain concepts have been reworked so as to encompass both finite and transfinite operations; the concepts of finite arithmetic do not automatically carry over into transfinite arithmetic. For instance `addition', although it is a concept that is applicable to both the finite and the transfinite, does not behave in the same way in both cases: the property of commutativity, for instance, is not assured for the addition of transfinite ordinals. A similar sort of restructuring of the concepts seems not to be possible for theology. As long as there is some insistence on preserving the mystery of the theological infinite, any agreement about restructuring concepts to encompass the infinite is prevented. Moreover, there are standards in mathematics for this restructuring of concepts — whether the extended concepts work. In theology, though, there is not even any agreement about whether concepts applied to God ought to `work'. If God essentially transcends our knowledge, then there is no reason to believe that the concepts we apply to God should `make sense'.

At this point we are faced with grave difficulties in defining the theological conception of the infinite. The theological conception of the infinite is defined by Descartes and Leibniz as a lack of limits. But there is no agreement about nor, apparently, any means of determining, how far this lack of limits reaches and what effect it has on predication. Furthermore, the conception of the unlimited is, according to mathematics, strictly independent from the infinite. And we have to ask how infinity could be an explanation for the difficulty in extending predicates from the mundane to the absolute, when there is no comparable degree of difficulty encountered in extending concepts from the finite to the infinite in mathematics. The link between the mathematical and the theological concepts of infinity seems at this point so tenuous that we might wonder whether `infinity', used of God, is not simply equivocal.

2.5 Infinity as metaphor

We might explore the possibility of a figurative attribution of infinity to God. Saying that God is infinite is meant to suggest that God shares the unending and mysterious quality of the infinite. Even the mathematical infinite remains a fascinating and compelling concept. Escher's pictures and some of Borges's stories, though based on aspects of mathematical infinity, have a power to cause delight or anxiety. Maybe it is this power, present even in the rationally defined concept, that is most relevant. Clearly, there is such a figurative use of infinity. I might say that something is infinitely beautiful to me: by this I should mean that I could never get tired of looking at the object and that its beauty comes from some as it were inexhaustible and mysterious source — mysterious in virtue of the fact that I cannot fully understand or articulate the reasons for the object's power over me. `Infinitely' here incorporates the mystery and the inexhaustibility, as well as suggesting a scope or a depth beyond the ordinary.

Perhaps there is a development of `infinite' as an attribute of God from the literal to the figurative. Before all the developments in mathematics — before our own century particularly, and before the seventeenth century altogether — the mathematical concept of the infinite was as tied to mystery as is the theological concept. In that context it was not senseless to say that God is literally infinite. But now, the mathematical concept of the infinite, and mathematical methods for dealing with it, make it impossible to suggest that God's infinity is the reason for any difficulties in thinking or talking about God. We cannot, now, simply stand in awe of the infinite and claim that it is not like anything else — mathematics shows that the infinite is in many respects not all that unlike the finite.

What we may be seeing here is a case where the term was originally used literally, and then retreated to a metaphorical status, because of the development and `secularization' of the infinite. Another possibility is that theological infinity has always been a mathematical metaphor conveying mystery and immensity, but that the metaphor has retained a meaning that has gradually been lost on its home ground. (Similar, perhaps, to the exemplar `Man is a wolf', which can be used to convey characteristics no longer believed to be possessed by wolves.)

The mathematical infinite cannot provide a direct, positive clarification of the meaning of the theological infinite. What the concept of the infinite can express about God does not lie in the gradual mathematical demystifying of the concept, nor even in the residual strange bits of the mathematical infinite, but rather in the wonder (or dread) we have felt in being introduced to infinite series or set theory, or in looking at Escher's pictures, or at the sky at night. Infinity fascinates us. The meaning of the metaphor of the infinite, as opposed to the useful operational infinite, is no more (or no less) than the mystery and wonder attached to the incomprehensibly immense. It may be that there is, historically, a literal source common to the mathematical and the theological infinite, but these concepts have diverged as the mathematical meaning has become more clear and less mysterious.

2.6 Incommensurability

We might still claim to find in infinity a reason for difficulty in attributing concepts to God, in virtue of the fact that the theological infinite is incommensurable with the finite as well as with the potential and actual infinities. As I am using `incommensurability' here, incommensurability can be said to involve an insurpassable gap, a discontinuity, the suspension of addition . . . we have a positive value that, no matter how often a certain amount is added to itself, cannot become greater than another positive value, and cannot . . . because they are the sort of value that, even remaining constant, cannot add up to some other value.¹² [James Griffin, Well-Being (Oxford: Clarendon Press, 1986), pp. 85ff.]

Whatever the theological infinite is, it is not constructible from the finite — not in fact and not in principle. We cannot get there from here; there is no process by which we would get to the theological infinite. This has been emphasized in the discussion of Descartes and Leibniz above. And we may wonder whether this insurpassable gap means that whatever measure we use for the finite and the `mundane' infinite, is not a measure for the theological infinite.

We could try saying that the same concepts cannot apply both to the finite and to the theological infinite, because of this incommensurability. The same concepts can, however, apply both to the finite and to the actual or potential infinite, because these types of infinite are constructible, at least in principle, from the finite. And then the fact that concepts stretch from the finite to the infinite in mathematics would not rule out the possibility of infinity's being an explanation for expressibility problems in theology.

A relevant point here is the idea that, while we know that God is good, we do not know what it is for God to be good: we do not know the truth-conditions or criteria for God's goodness. According to this idea, just adding on to the mundane concept of goodness will not get us to a real understanding of God's goodness. God's goodness is not just bigger, so to speak, than human goodness; it is different, on a different scale altogether. If I, for instance, were to have power added to me, even to infinity, I can imagine I should be able to move large pieces of furniture without help, work for hours and hours, and so forth. But this is not what `infinite power' means for God. If I had infinite power, I should have infinite human power; I should still not be able to create something in its being ex nihilo. Again, the point is that God's power is not limited by the nature of God, as my power is limited by my (human) nature. We might wonder if there is a sort of conceptual gap here: while we can imagine what it would be like (give the truth-conditions) for a mundane quality to be increased to infinity, we cannot grasp what is infinite on another scale altogether.

This line of thought, though, is also questionable. It need not be impossible to grasp what is infinite on another scale altogether; it may simply be that we have not yet found the scale, not found a useful model. Even if two things are incommensurable in the sense defined, it need not follow that the same concepts do not apply to both. Certainly my intellect is incommensurable with Leibniz's in this sense: no matter how many of me were working together, we should in all likelihood not have invented calculus — but the same concepts of intellect apply to both me and Leibniz.

It seems that incommensurability, too, can be seen as a figurative expression of God's transcendence. God's infinity is said to transcend mundane infinity, the sort of infinity that we can construct and grasp, not because we are barred from reaching the theological infinite by some practical considerations, as someone might say that we are barred from reaching the actual infinite. Rather, we cannot reach the theological infinite because we have no process for constructing it, no means of reaching it.

III. CONCLUSION

If `infinite', used of God, is a figurative expression of mystery, immensity, and transcendence, then it is not a cause or reason for problems with expressibility. `Absolutely infinite' does not give us a new and useful piece of knowledge about God, the way that `denumerably infinite' does give us new and useful knowledge about the rational numbers. It is not so much that we `discover' that God is infinite, and thereby discover a good explanation for the difficulties of predication that we have experienced. We might just as well say that, experiencing God as mysteriously unlimited and, so to speak, unimaginably large, we attribute to God a term that expresses — among other things — wonderful and fascinating mystery and inexhaustibility in other matters.

It may be that the proposition `God is infinite' can be taken literally only when infinity in general is shrouded in mystery. When infinity is `secularized' and mathematical infinity is given an increasingly clear and unmysterious meaning, `infinite' can be understood of God only figuratively. In this figurative meaning, `infinite' is meant to suggest the ever-present fascination and, as it were, unwieldy vastness of the infinite. We cannot somehow extend the mathematical concept of the infinite in order to gain a deeper understanding of the nature of God. Instead, comparison of the mathematical with the theological concept brings into light the experience of God as the mysterious unspeakable.¹³ [I am grateful to Hans Herzberger for his comments on earlier drafts of this material. I am also grateful to Edwin Mares for his suggestions.]

Department of Philosophy,
McMaster University,
Hamilton, Ontario,
Canada, L8S 4K1