GEORG CANTOR

His Mathematics and Philosophy of the Infinite

Joseph Warren Dauben

HARVARD UNIVERSITY PRESS

Cambridge, Massachusetts
and London, England
1979

CHAPTER 6

Cantor's Philosophy of the Infinite

Cantor made philosophy an equal and intentional partner to mathematics in his Grundlagen einer allgemeinen Mannigfaltigkeitslehre. In the German version issued as a separate monograph by Teubner in 1883, a simple introduction was added in which he stressed that the mathematical and the philosophical sections were inextricably connected.¹ In Cantor's view, the Grundlagen was much more than a strictly mathematical presentation of his new transfinite set theory. It offered as well his first published defense of the actual infinite, a concept which most philosophers, theologians and mathematicians had traditionally opposed.

Philosophers had been wary of the paradoxical nature of the infinite since the Pre-Socratics first began to explore its many contradictory forms. Aristotle's solution was generally followed, which simply rejected the use of completed infinities. Christian theologians were also opposed to the actual infinite; for the most part they regarded the idea as a direct challenge to the unique and absolutely infinite nature of God. Finally, mathematicians generally followed the philosophers in avoiding any application of the actual infinite, and their reluctance stemmed from the apparent inconsistencies such concepts always seemed to introduce. Gauss, in a celebrated letter to Heinrich Schumacher, expressed in most authoritative terms his opposition to use of such infinities:

But concerning your proof, I protest above all against the use of an infinite quantity [Grösse] as a completed one, which in mathematics is never allowed. The infinite is only a façon de parler, in which one properly speaks of limits.²

Cantor was well aware that his new theory of infinite sets and transfinite numbers faced opposition, much of it traditional and of long standing. One goal

A portrait of Cantor in middle life. In the possession of Wilhelm Stahl.

of the Grundlagen was to demonstrate that there was no reason to accept the old objections to completed, actual infinities and that it was possible to answer mathematicians like Gauss, philosophers like Aristotle, and theologians like Thomas Aquinas in terms they would find impossible to reject. In the process Cantor was led to consider not only the epistemological questions which his new transfinite numbers raised but to formulate as well an accompanying metaphysics. Arguing the mathematical consistency of the new theory, and thereby asserting its legitimacy, was not enough. He felt compelled to defend his work from any form of attack, on whatever level, and therefore he was anxious to consider philosophical and theological objections that might be raised against the concept of actual infinities.

PHILOSOPHY OF THE INFINITE

Cantor believed that opposition to the use of actual infinities in mathematics, philosophy, and theology was based upon a common and pervasive error. Whatever mathematicians may have assumed in the past, finite properties could not be predicated in all cases of the infinite. Such attempts led inevitably to contradictions and to misunderstandings. In explaining this to Vivanti in a letter of 1886, he pointed to Aristotle as the source for the medieval dogma: "infinitum actu non datur,"³ something Cantor described as a basic tenet of the scholastics. As the inspiration for centuries' worth of opposition to the actual infinite, Aristotle required explicit confrontation. His assumption that there were only finite numbers, which led to the conclusion that only enumerations of finite sets were possible, precluded any consideration of infinite numbers from the start.

A typical argument used by Aristotle and by the scholastics involved the "annihilation of number."⁴ Were the infinite admitted, it was said that finite numbers would be swallowed up by any infinite number or magnitude. For example, given any two finite numbers a and b, both greater than zero, their sum a + b > a, a + b > b. However, if b were infinite, no matter what finite value a might assume, a + 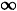= 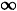, and this seemed contrary to a well-known and basic property which the addition of any two positive numbers ought to exhibit. It was in this sense that any infinite number was thought to "annihilate" any finite number, and because this appeared to violate the way in which numbers were understood to behave, infinite numbers were consequently rejected as being inconsistent.

Cantor condemned this kind of argument, however, on the grounds that it was fallacious to assume that infinite numbers must exhibit the same arithmetic characteristics as did finite numbers. Moreover, by direct appeal to his theory of transfinite ordinal numbers, Cantor could demonstrate that infinite numbers were susceptible of modification by finite numbers. In fact, the distinction between Cantor's w and w + 1 showed expressly that finite numbers could be added to infinite numbers without being "annihilated." Thus Cantor believed that Aristotle was quite mistaken in his analysis of the infinite, and that his authority was exceedingly detrimental.⁵

Having dealt with Aristotle and the scholastics, Cantor undertook an investigation of other works by some of the most impressive thinkers of the seventeenth century, a century that witnessed serious and often profound analysis of the nature of infinity. He suggested that anyone interested in such things would do well to consult Locke, Descartes, Spinoza, and Leibniz, while Hobbes and Berkeley were highly recommended as additional reading.⁶ These writers had produced the most convincing criticisms known to Cantor of the actual infinite. If he could demonstrate their error in rejecting completed infinities, then he was certain that his transfinite numbers could easily withstand criticism of a similar or less penetrating sort. Since he believed that refutation of systematic and coherent knowledge (as he characterized the thought of the seventeenth century) could only be done, legitimately, in terms of such systems and since God was inevitably called upon in the judgments of the seventeenth century, Cantor felt obliged to make similar considerations.

With this in mind, he summarized the position most commonly encountered in the seventeenth century: that number could only be predicated of the finite. The infinite, or Absolute, in this view, belonged uniquely to God.⁷ Uniquely predicated, it was also beyond determination, since once determined, the Absolute could no longer be regarded as infinite, but was necessarily finite by definition. Cantor's inquisitive "how infinite" was an impossible question. To minds like Spinoza and Leibniz, the infinite in this absolute sense was incomprehensible, as was God, and therefore any attempt to assign a basis for determining magnitudes other than merely potential ones was predestined to fail.

Moreover, following Aristotle, the "annihilation" of finite quantities by completed infinities (were they to exist) seemed completely contradictory, and consequently no concept of infinite numbers could be accepted in mathematics. Cantor criticized this refusal to predicate anything of the absolute in terms of number, just as he had in showing the inadequacy of Aristotle's position on the same point, by showing that such conclusions depended upon a circular argument, a petitio principii. It was improper to assume that infinite numbers should be constrained to follow principles established for finite numbers. As he explained, though 1 + w = w might be said to annihilate the unit on the left, (w) + 1 = (w + 1) just as clearly did not.⁸ Added on the right the unit did in fact, under the rules of transfinite arithmetic, modify the actually infinite number w.

Although Cantor at times made it seem as if he were the first and only mathematician to have taken the absolute infinite seriously, he nevertheless drew some solace from two of his predecessors.⁹ Both were important figures in the historical development of the concept of infinity, and both had written on the mathematical and philosophical consequences of the actual infinite. One of these was G.W. Leibniz, the other was Bernhard Bolzano.

Leibniz was particularly difficult because his opinions concerning the infinite

seemed different depending upon occasion and context. As Cantor showed from various citations, Leibniz frequently denied any belief in the absolute infinite. However, in several instances Leibniz did advance a useful and significant distinction between the actual infinite and the absolute infinite, and Cantor was happy to claim him as a supporter of the former, at least in the following passage:

I am so in favor of the actual infinite that instead of admitting that Nature abhors it, as is commonly said, I hold that Nature makes frequent use of it everywhere, in order to show more effectively the perfections of its Author. Thus I believe that there is no part of matter which is not -- I do not say divisible -- but actually divisible; and consequently the least particle ought to be considered as a world full of an infinity of different creatures.¹⁰

Cantor developed this idea to great advantage several years later, particularly in attempting to obviate the confrontation some had feared between a theological interpretation of the infinite and Cantor's new transfinite numbers.

Unlike Leibniz, Bolzano was an unequivocal champion of the absolute infinite.¹¹ Cantor particularly admired Bolzano's attempt to show that the paradoxes of the infinite could be explained, and that the idea of completed infinities could be introduced without contradiction into mathematics. In fact, Bolzano's Paradoxien des Unendlichen, published in 1821, received high praise from Cantor for having done an important service to mathematics and philosophy alike.

Even so, Cantor criticized Bolzano's treatment of the infinite for two reasons. Not only was Bolzano's concept of the actual infinite mathematically unclear, but the important ideas of power and the precise concept of numbering were never developed.¹² Though in certain instances one could find suggestions of both ideas, they were never accorded lucid and independent development. These were essential concepts, Cantor stressed, for a proper understanding of infinite number, and without them, no completely successful theory of the actual infinite was possible. Nevertheless, despite such reservations and disagreements with certain particulars of Bolzano's program, Cantor was nevertheless impressed by the boldness and the audacity with which he defended the actual infinite in mathematics.

One feature of Bolzano's work which particularly impressed Cantor was the distinction he made between categorematic (actual) and syncategorematic (potential) infinities. The Grundlagen placed much stress on this point, and in his more philosophical papers (published several years later), Cantor went even further in exposing the faulty assumptions of those who failed to admit the distinction. For example, among contemporary German philosophers opposed to the idea of completed infinities, Cantor singled out John Frederick Herbart and Wilhelm Wundt as prime offenders. Their preoccupation with potential infinities precluded any satisfactory discussion of the actual infinite. In a letter to the Swedish mathematician and historian Gustav Eneström, Cantor summarized his opposition as follows:

All so-called proofs against the possibility of actually infinite numbers are faulty, as can be demonstrated in every particular case, and as can be concluded on general grounds as well. It is their that from the outset they expect or even impose all the properties of finite numbers upon the numbers in question, while on the other hand the infinite numbers, if they are to be considered in any form at all, must (in their contrast to the finite numbers) constitute an entirely new kind of number, whose nature is entirely dependent upon the nature of things and is an object of research, but not of our arbitrariness or prejudices.¹³

Herbart was particularly open to Cantor's criticism. By defining the infinite in terms which admitted only potential forms of infinity, there was no way Herbart could have consistently allowed the idea of a completed or an actual infinity. Cantor believed that the actual infinite had to be studied without such arbitrariness or prejudice. Cantor once said that the nature of things had to be taken as given, and he was certain that the nature of things both abstractly in mathematical terms and concretely in physical terms affirmed the existence of his transfinite numbers.¹⁴ Moreover, the connections between the two, the abstract and the concrete, provided yet another level upon which Cantor hoped to justify his new theory.

METAPHYSICS AND CANTOR'S MATHEMATICS

Whenever Cantor spoke of metaphysics he meant the philosophical study of the relations between the constructs of mind and the objects of the external world. Thus the study of the abstract theory of the transfinite numbers was the business of mathematics, but the study of the realization or embodiment of the transfinite numbers in terms of the objects of the phenomenological world was the concern of metaphysics. And so metaphysics assumed its place in Cantor's continuing program to establish the legitimacy of his new theory, particularly in the years following publication of the Grundlagen.

In the Grundlagen itself, Cantor was careful to distinguish between real (reellen) numbers and real (realen) numbers, though it was a distinction lost in both the original French and in the recent English translations of the work.¹⁵ Considering the French version which appeared in Acta Mathematica, this is not surprising, for Mittag-Leffler had specifically requested that Cantor prepare a version of his monograph eliminating entirely all philosophical aspects of his arguments in favor of the transfinite numbers. Since the contrast between the real and real numbers was essentially one of metaphysical significance to Cantor, the French version appeared without any emphasis upon the reality which he attributed to the new concepts being advanced.

Even so, the distinction was of major importance to Cantor for epistemological reasons. It was essential to differentiate between the reellen Zahlen, real numbers as opposed to the complex numbers in a formal mathematical sense, and realen Zahlen, real, actual numbers which enjoyed more than a purely formal existence. In fact, he insisted that his transfinite numbers were real in the same sense that the finite whole numbers might be regarded as real.¹⁶ Since the positive integers were taken to have an objective existence in terms of actual sets of finitely many objects, exactly the same was true for his transfinite numbers, because they too were derived from actual sets of infinitely many objects.

Thus transfinite numbers reflected, in terms of their origins, the same character as did finite numbers, although Cantor's new numbers were grounded in infinite rather than in finite sets. And, just as the finite whole numbers possessed an objective reality, so did the transfinite numbers. Their existence was naturally reflected in the matter and space of the physical world, and in the infinities of concrete objects. There was a particularly interesting passage elaborating this idea at the very end of a paper he published in the Acta Mathematica in 1885. Mittag-Leffler had suggested that Cantor demonstrate the utility of his new concepts by suggesting some possible applications of transfinite set theory to other branches of science.¹⁷ Cantor did so by introducing two hypotheses concerning the nature of matter and the aether. Utilizing a consciously Leibnizian terminology, he raised two questions: what was the power [Mächtigkeit] of the set of all monads that were material? Similarly, what was the power of all monads comprising the aether? Cantor replied by saying that for years he had held the hypothesis that the set of all material monads was of the first power, while the set of all aetherial monads was of the second power.¹⁸ He claimed there were many reasons to support this view, but he did not produce any at the time. Instead, he went on to suggest that transfinite set theory, applied in this way, would be of great benefit to mathematical physics and could help solve problems of natural phenomena including the chemical properties of matter, light, heat, electricity, and magnetism.

Just as the irrational numbers were in a sense concretized by virtue of their geometric representation (the 2^1/2 by the diagonal of a square, for example), Cantor found a similar objectivity for his transfinite numbers in the material world. This material verification of the transfinite numbers was achieved by virtue of the actually infinite sets of monads, corporeal or aetherial, in which the transfinites were reflected. Though he never placed primary emphasis upon this concrete, metaphysical component of his thinking in trying to justify his theory, he did believe it to be a reasonable auxiliary. In his own mind, the applications of transfinite numbers in physical terms was direct evidence of their very real existence.¹⁹

There were other approaches, too, by which he argued the objective reality of his transfinites. He offered a particularly interesting argument whereby he turned the position of finitists like Kronecker to his own ends. If the integers were granted real and objective status in mathematics, Cantor reasoned that the same was then true for his transfinite numbers. Finitists, who only allowed arguments of the sort: "For any arbitrarily large number N there exists a number n > N," necessarily presupposed (said Cantor) the existence of all such numbers n > N, taken as an entire, completed collection which he called the Transfinitum.

In a lengthy footnote to remarks which he had made at a meeting of the Gesellschaft Deutscher Naturforscher und Aerzte in Freiburg during September 1883, he elaborated his metaphor of the road, which illustrated in a graphic and charming way his argument for the very real and necessary existence of the actual infinite:

Apart from the journey which strives to be carried out in the imagination [Phantasie] or in dreams, I say that a solid ground and base as well as a smooth path are absolutely necessary for secure traveling or wandering, a path which never breaks off, but one which must be and remain passable wherever the journey leads.²⁰

In strictly mathematical terms, Cantor translated this as follows: "Thus every potential infinity (the wandering limit) leads to a Transfinitum (the sure path for wandering), and cannot be thought of without the latter."²¹ Cantor, in all seriousness, believed that his theory of the transfinite numbers was the "Highroad of the Transfinites," and that it was absolutely necessary for the existence and applicability of the potential infinite. In a letter to the Italian mathematician Vivanti, he asserted the existence of the transfinite numbers even more emphatically.²² In the more general language of domains, be they in algebra, number theory, or analysis, the domain of values had to be taken, he insisted, as actually infinite.

This position, however, cleverly led Cantor to press another reason for the justification of his transfinite numbers. Once the existence of absolutely infinite sets was established, then the transfinite numbers were a direct consequence. He explained his reasons for this assertion in the above-mentioned lecture he presented in Freiburg, in 1883. Since finishing the Grundlagen he had considerably sharpened both his concept of power and that of Anzahl, or ordinal number, by defining them as general concepts abstracted from given, existing sets.²³ This development (one of great significance for Cantor's evolution of transfinite set theory in the years following the Grundlagen) is discussed in greater detail in the following chapter, but for now it is enough to appreciate how he had come to regard the transfinite numbers as naturally produced, by abstraction, from the existence of actually infinite sets. For example, "By the numbering [Anzahl] or the ordinal number of a well-ordered set I mean the general concept or universal [Allgemeinbegriff, Gattungsbegriff] which one obtains by abstracting the character of its elements and by reflecting upon nothing but the order in which they occur."²⁴

Thus, if one admitted the existence of infinite sets, the transfinite numbers followed as little more than a direct consequence. To support further the reasonableness of such thinking, Cantor reexamined the grounds for granting the irrational numbers mathematical legitimacy. He emphasized the similarities which bound the established, acceptable irrationals with his new, unorthodox transfinites:

The transfinite numbers themselves are in a certain sense new irrationals, and in fact I think the best way to define the finite irrational numbers is entirely similar; I might even say in principle it is the same as my method described above for introducing transfinite numbers. One can absolutely assert: the transfinite numbers stand or fall with the finite irrational numbers; they are alike in their most intrinsic nature [inneresten Wesen]; for the former like these latter (numbers) are definite, delineated [abgegrenzte] forms or modifications () of the actual infinite.²⁵

To define the irrational numbers, infinite collections of rational numbers had been required. Believing that any potentially infinite collection necessarily presupposed the existence of infinite collections, while asserting that the concept of number proceeded directly by abstraction from the existence of a given set, finite or infinite, Cantor concluded that the existence and reality of the transfinite numbers was immediate. The only further requirement was consistency. As long as new concepts were not inconsistent, there was no reason why they should not find acceptance and application in mathematics.

CONSISTENCY AND THE IMPORTANCE OF CANTOR'S FORMALISM: IRRATIONALS, TRANSFINITES, AND INFINITESIMALS

Though Cantor believed in the objective reality of his transfinite numbers and argued that their existence was confirmed directly by abstraction from the existence of infinite sets, he did not believe that mathematicians needed either to consider or to accept such arguments. If one wished to do so, such lines of reasoning might be regarded as compelling, but they were not essential. For mathematicians, only one test was necessary: once the elements of any mathematical theory were seen to be consistent, then they were mathematically acceptable. Nothing more was required:

In particular, in introducing new numbers, mathematics is only obliged to give definitions of them, by which such a definiteness and, circumstances permitting, such a relation to the older numbers are conferred upon them

that in given cases they can definitely be distinguished from one another. As soon as a number satisfies all these conditions, it can and must be regarded as existent and real in mathematics. Here I perceive the reason why one has to regard the rational, irrational, and complex numbers as being just as thoroughly existent as the finite positive integers.²⁶

Logical consistency was the touchstone which Cantor applied to any new theory before declaring it existent and a legitimate part of mathematics. Though he had argued the theoretical consistency of his transfinite numbers, he was not content to leave that as their only justification. He had cleverly devised a series of arguments, leading directly from the more generally accepted irrational numbers to the corresponding mathematical reality of the transfinite numbers as well. Realizing that more mathematicians might find it initially easier to admit the consistency and reality of the irrational numbers, he suggested that it was then only a short step to accepting his new transfinite numbers without reservation.

As he had said before, one could not accept the irrationals and reject the transfinites. Ontologically, their mathematical status was the same. Both were defined in terms of infinite sets, by similar procedures. Since he took his transfinite numbers to be consistently defined, with regular number-theoretic properties established in the Grundlagen, there were no grounds to deny his new theory. This kind of formalism, stressing the internal conceptual consistency of his new numbers, was all mathematicians needed to consider before accepting the validity of the transfinite numbers.

Cantor's formalism was nowhere better represented than by his lifelong opposition to infinitesimals. Contrary to the efforts of mathematicians like du Bois-Reymond, Stolz, and Vivanti who had seriously attempted to establish theories of actual infinitesimals, Cantor believed that his transfinite numbers could be called upon to demonstrate the inadmissibility of such ideas.²⁷ He used the results of his theory of ordinal numbers, the numberings of well-ordered sets, to show the contradictory nature of any assumption of the existence of infinitesimally small linear magnitudes.

There is even some irony in Cantor's position. To many mathematicians, his theory of actually infinite transfinite numbers seemed to justify intrinsically the infinitely small as well as the infinitely large. Benno Kerry, in a review of the Grundlagen, expressed his own faith in a formal definition of infinitesimals in a footnote:

In my opinion a formal definition of definite, infinitely small numbers is indeed given in fixing the greatest of such numbers as one which produces the sum 1 by adding itself to itself w times; the next smaller is then the one which produces 1 by adding itself to itself w - 1 times, etc. The definite, infinitely small numbers would accordingly be denoted as:

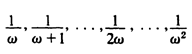
etc. Of course whether numbers so defined have any empirical applicability is not decided here.²⁸

Taken as reciprocals, it seemed that the transfinite numbers ought to provide an immediate basis for a theory of actual infinitesimals. But to Cantor's mind, such a step was irresponsible and under no circumstances could it be rigorously justified. In the Grundlagen, he tactfully expressed his skepticism of infinitesimals, saying only that attempts to consider the infinitely small in absolute terms were unsound and without purpose. Later he remarked, however, that he had been too reserved in the Grundlagen by failing to deny explicitly the existence of actually infinitesimal quantities.²⁹

In 1887 Cantor explained his rejection of any consideration of infinitesimals on purely formal grounds in a letter to his old teacher in Berlin, Karl Weierstrass.³⁰ Cantor presented his contention directly in the form of a theorem:

Non-zero linear numbers V (in short, numbers which may be thought of as bounded, continuous lengths of a straight line) which would be smaller than any arbitrarily small finite number do not exist, that is, they contradict the concept of linear numbers.³¹

Cantor intended to refute attempts (made by Stolz and du Bois-Reymond) to produce infinitesimals by discounting the Archimedean Axiom. This axiom asserted that given any real numbers a<b, it was possible, for some arbitrarily large neN, to ensure that na>b. Cantor based his proof of the impossibility of infinitesimals upon the concept of linear numbers. Numbers were linear if a finite or infinite number of them could be added together to produce yet another linear magnitude. If V were an infinitesimal, Cantor argued that V · v, even if v were transfinite, would remain arbitrarily small, less than any linear quantity. Thus he asserted: "that V cannot be made finite by any multiplication, however great, not even an actually infinite one, and thus it certainly cannot be an element of finite numbers."³²

On the strength of this conclusion, Cantor went on to demonstrate that the Axiom of Archimedes was no axiom, but a proposition about the system of real numbers that could be proven. Non-Archimedean systems could not be generated, he argued, simply by discarding the axiom, since it was not an axiom at all. As long as he believed it was actually a theorem following directly from the concept of number itself, infinitesimals were necessarily contradictory.

In 1893 Vivanti, the Italian mathematician, wrote to Cantor suggesting that his rejection of infinitesimals was unjustified. As du Bois-Reymond had shown, "the orders of infinity of functions constitute a class of one-dimensional magnitudes, which include infinitely small and infinitely large elements. Thus there is no doubt that your [Cantor's] assertions cannot apply to the most general concept of number."³³

In defending his point of view, Cantor wrote back to Vivanti with the vitriolic remark that to the best of his knowledge, Johannes Thomae was the first to "infect mathematics with the Cholera-Bacillus of infinitesimals."³⁴ Paul du Bois-Reymond, however, was soon to follow. Cantor claimed that in systematically extending Thomae's ideas, du Bois Reymond found "excellent nourishment for the satisfaction of his own burning ambition and conceit."³⁵ Cantor went on to discredit du Bois-Reymond's infinitesimals because they were self-contradictory, since he rejected without compromise the existence of linear numbers which were non-zero yet smaller than any arbitrarily small real number. Infinitesimals, Cantor replied, were complete nonsense. He reserved his strongest words for du Bois-Reymond's Infinitäre Pantarchie and his orders of infinitesimals: "Can one still call such things numbers? You see, therefore, that the `Infinitäre Pantarchie,' of du Bois-Reymond, belongs in the wastebasket as nothing but paper numbers!"³⁶ Cantor placed the theory of actual infinitesimals on a par with attempts to square the circle, as impossible, sheer folly, belonging in the scrap heap rather than in print. Ironically, much of Cantor's criticism could have been turned as effectively against the transfinite numbers as against infinitesimals. And his rejection of infinitesimals was certainly fallacious in its reliance upon a petitio principii. Having assumed that all numbers must be linear, this was equivalent to the Archimedean property, and thus it was no wonder that Cantor could "prove" the axiom. The infinitesimals were excluded by his original assumptions, and his proof of their impossibility was consequently flawed by its own circularity.

In addition to the arguments Cantor made explicit, there were other persuasive reasons for his rejection of infinitesimals. Mittag-Leffler had once asked him about the possible existence of infinitesimals as numbers interpolated between the rational and irrational numbers.³⁷ But Cantor believed in the completeness of the finite real numbers, in terms of rational and irrational numbers alone. His work in analysis and set theory had always assumed the reciprocal and unique correspondence between the real numbers and points on the real line. His continuum hypothesis, too, would only have been complicated by admitting infinitesimals as an entirely new sort of number, sandwiched between the rational and irrational numbers. Were there infinitesimals, somehow, in addition to the standard real numbers, then the continuum hypothesis might even prove to be false. There would have been many more numbers to contend with than the familiar set of reals, and this would have made the likelihood of his hypothesis more doubtful and certainly more complex.

Nevertheless, the overriding basis for Cantor's rejection of infinitesimals rested upon the question of consistency. On the basis of his own definition of linear quantity, the infinitesimals were contradictory. Hence they were unacceptable. The argument was the clearest expression of his formalist justification for ideas in mathematics. Ultimately, appeals to consistency were sufficient to advance the reality and legitimacy of any sort of real number -- rational, irrational, complex, or transfinite. The true nature of Cantor's position concerning the nature of mathematical ontology in general, and the legitimacy of his transfinite numbers in particular, was only vaguely discernible in the Grundlagen itself. But in the succeeding years, as Cantor's interests became more philosophical, this kind of formalism became increasingly apparent.

THE NATURE OF MATHEMATICS

Cantor reinforced his study of the philosophical status of his new numbers with a simple analysis of the familiar and accepted natural whole numbers. For both finite and infinite integers, they could be considered in essentially two ways. Insofar as they were well-defined in the mind, distinct and different from all other components of thought, they served "in a connectional or relational sense to modify the substance of thought itself." This reality, which the whole numbers consequently assumed, he described as their intrasubjective or immanent reality.³⁸ In contradistinction to this immanent reality was the reality numbers could assume concretely, manifest in objects of the physical world. He explained further that this second sort of reality proceeded from whole numbers as expressions or images of processes in the world of physical phenomena. This aspect of the whole numbers, be they finite or infinite, he termed transsubjective or transient.³⁹

Cantor asserted the reality of both the physical and ideal aspects of the number concept. These dual realities, in fact, were always found in a joined sense, insofar as a concept possessing any immanent reality always had a transient reality as well.⁴⁰ It was one of the most difficult problems of metaphysics to determine the nature of the connection between the two.

Cantor ascribed the necessary coincidence of these two aspects of number to the unity of the universe itself.⁴¹ This meant that it was possible to study only the immanent realities, without having to confirm or conform to any objective content. This set mathematics apart from all other sciences and gave it an independence that was to imply great freedom for mathematicians in the creation of mathematical concepts. It was on these grounds that Cantor offered his now famous dictum that the essence of mathematics is its freedom. As he put it in the Grundlagen:

Because of this extraordinary position which distinguishes mathematics from all other sciences, and which produces an explanation for the relatively free and easy way of pursuing it, it especially deserves the name of free mathematics, a designation which I, if I had the choice, would prefer to the now customary "pure" mathematics.⁴²

Cantor thus asserted the freedom of mathematics to accept the creation and application of new ideas solely on the grounds of intellectual consistency. Though there were counterparts to the immanent reality of number in the phenomenological world, that did not matter. Instead, the formal consistency of mathematical ideas in the mind provided the ultimate criterion for Cantor in determining the advance of mathematics. Its application to physical phenomena of the external world was of considerable but subsidiary importance.

Mathematics was therefore absolutely free in its development, and bound only to the requirement that its concepts permit no internal contradiction, but that they follow in definite relation to previously given definitions, axioms, and theorems. On these grounds, what were the criteria for introducing new numbers? The matter rested entirely in terms of definition. So long as new numbers were distinct and could be distinguished from other kinds of numbers, as well as from each other, then a new number was defined and must be taken as existing.

The only possible objection to this doctrine of freedom in mathematics, said Cantor, might be the arbitrary creation of new ideas without correctives. But there were, he insisted, correctives nonetheless. If an idea was fruitless or unnecessary, this quickly became evident, and by reason of failure, was abandoned or forgotten.⁴³ Alternatives, like the safe but limiting restriction of mathematics to the realm of finite numbers advocated by Kronecker and his followers, were very dangerous from Cantor's point of view. Any restriction or narrowness in mathematics would have direct and obvious consequences. Controls and artificial philosophical presuppositions retarded or even prevented any growth of mathematical knowledge. Cantor appealed to the great and legendary figures of the history of mathematics to lend support to his contention.

Without the freedom to construct new ideas and connections in mathematics, Gauss, Cauchy, Abel, Jacobi, Dirichlet, Weierstrass, Hermite, and Riemann would never have made the significant advances they did. Kummer would never have been able to formulate his ideal numbers, and consequently the world would be in no position, Cantor added with a note of cunning, to appreciate the work of Kronecker and Dedekind.⁴⁴

Mathematics, Cantor believed, was the one science justified in freeing itself from any metaphysical fetters. Applied mathematics and theoretical mechanics, on the contrary, were metaphysical in both their content and goals.⁴⁵ Any attempt to free them from metaphysical substrata resulted in nothing but idle speculation describing worlds without substance. But mathematics, by virtue of its independence from any constraints imposed by the external reality of the spatial-temporal world, was quite free. Its freedom, as Cantor insisted was its essence.

THE CRISIS OF THE CONTINUUM AND CANTOR'S THEORY OF ORDER TYPES

Cantor once described the terrain of set theory, as he regarded it shortly after the first part of the Grundlagen had been published, as a terra incognita.⁴⁶

Unquestionably, the most perplexing lacuna was the continuum hypothesis. Though he had tried repeatedly to show that the real numbers were equal in power to the second number class (II), he had never succeeded in proving the conjecture. Every time a new solution seemed promising or near perfect, something always turned up to dash his hopes. In May 1883 he wrote to Mittag-Leffler, saying that he had worked on the problem for a long time and yet every proof he had found eventually revealed mistakes or errors that required new beginnings.⁴⁷

While Cantor was continually frustrated by his failure to resolve the continuum hypothesis, he was also having to suffer Kronecker's campaign to discredit transfinite set theory. Cantor complained, in correspondence with the French mathematician Hermite, that Kronecker was attacking his work and calling it "humbug."⁴⁸ Shortly before Christmas 1883 Cantor was so angered by these attacks that he wrote directly to the Ministry of Education, hoping to annoy Kronecker by applying for a position in Berlin available the following spring.⁴⁹ Cantor was convinced that the time might at last have come when Berlin needed him. In his opinion he was the only person in Germany who could be said to know all of mathematics, both old and new. He was convinced that his historical interests incorporated explicitly as part of the Grundlagen represented special preparation and gave him a unique appreciation for mathematics. He also felt strongly that he deserved the honor of a position at a German university known for its great mathematicians: Göttingen, or preferably, Berlin. But in a letter to Mittag-Leffler of December 30 he admitted that the application in Berlin would come to nothing.⁵⁰ He had heard from Weierstrass that the obstacles were largely financial, owing to Kronecker's large salary. Nonetheless, the letter to Mittag-Leffler also provided Cantor with another occasion to reiterate the bitterness he felt toward his position at Halle and to emphasize how poorly he was compensated there in comparison with Schwarz, Fuchs, Kronecker, and other of Cantor's least favorite colleagues. The following short remarks reveal how vehement Cantor could be in his judgment of Kronecker and of Kronecker's allies in Berlin:

You understand quite rightly the meaning of my application; I never thought in the least I would actually come to Berlin. But since I plan to do so eventually and since I know that for years Schwarz and Kronecker have intrigued terribly against me, in fear that one day I would come to Berlin, I regarded it as my duty to take the initiative and turn to the Minister myself. I knew precisely the immediate effect this would have: that in fact Kronecker would flare up as if stung by a scorpion, and with his reserve troops would strike up such a howl that Berlin would think it had been transported to the sandy deserts of Africa, with its lions, tigers, and hyenas. It seems that I have actually achieved this goal!⁵¹

If Cantor had sought to annoy Kronecker, Kronecker returned the challenge masterfully. There can be no doubt that Kronecker's subsequent maneuver, following in early January 1884, certainly had an overwhelming effect upon Cantor. Kronecker wrote to Mittag-Leffler asking to publish in the Acta Mathematica a short paper on his position with regard to certain mathematical conceptions in which he would show "that the results of modern function theory and set theory are of no real significance."⁵² At first Cantor was mildly receptive to the idea, believing that at last it would bring Kronecker's opposition into the open, where it could be directly countered, and presumably rejected. But Cantor began to have second thoughts, and he feared that Kronecker might reduce their differences to personal polemics. To Cantor it seemed that Kronecker, by wanting to publish in Acta Mathematica, was trying to drive him out of the one journal in which he had found a sympathetic editor, just as Kronecker years earlier had tried to prevent Cantor from publishing any of his work in Crelle's Journal. The analysis Cantor made of the matter to Mittag-Leffler was highly skeptical of Kronecker's intentions. He warned that all was surely not what it seemed, and added for good measure the maxim: "timeo Danaos et dona ferentes."⁵³ Should any polemical writings appear in the Acta Mathematica under Kronecker's signature, Cantor threatened that he would withdraw his support from the journal.⁵⁴ Though he was soon to make good this threat for other reasons, the matter did not come to such an end because of Kronecker's paper. Apparently, Kronecker never sent anything for Mittag-Leffler's perusal, and certainly no provocative confrontation materialized in the Acta Mathematica. But the threats Cantor was willing to make, even to his friend Mittag-Leffler, showed how vindictive he could be in response to the conspiracy he felt was brewing against his work under the auspices of a single man: Leopold Kronecker.

By the early part of 1884 Cantor was again at work on the continuum hypothesis, but he found it as intransigent as ever. On April 4, 1884, he wrote to Mittag-Leffler and announced that while the problem had been reduced to showing that perfect sets were equivalent in power to the second number class (II), the continuum hypothesis still had not been solved.⁵⁵ Though he did not seem to register despondency over his prolonged inability to solve the continuum conjecture, it must nevertheless have been an ever-present source of frustration. Having said in the last paragraph of the sixth paper of the Punktmannigfaltigkeitslehre series that he expected a solution in the near future, he was committed to producing one.⁵⁶

However, the strain of such anxieties was apparently more than Cantor could bear, and in the spring of 1884 he suffered the first of his serious nervous breakdowns. The illness came upon him swiftly and unexpectedly.⁵⁷ Evidence in a letter to Felix Klein suggests that it must have occurred shortly after May 20, 1884, and apparently lasted somewhat more than a month. By the end of June he was sufficiently recovered to write to Mittag-Leffler but complained that he lacked the energy and interest to return to rigorous mathematical thinking and was content to take care of trifling administrative matters at the university. He felt capable of little more. But it is significant that Cantor also

added that he was anxious to return to work and would prefer his research to confining himself to the preparation of his lectures:

I thank you heartily for your kind letter of May 15; I would have answered it sooner, but recently I have not felt so fresh as I should, and consequently I don't know when I shall return to the continuation of my scientific work. At the moment I can do absolutely nothing with it, and limit myself to the most necessary duty of my lectures; how much happier I would be to be scientifically active, if only I had the necessary mental freshness!⁵⁸

In fact, as soon as he had recovered sufficient strength, Cantor set off for his favorite vacation resort in the Harz mountains and returned to his analysis of perfect sets. He also undertook the bold step of writing (on August 18, 1884) directly to Kronecker and attempted to put their differences aside.

Kronecker's response was as positive as anyone might have expected, but the attempted peace was not to last.⁵⁹ Though Cantor tried to explain several technical details of his new theory in a second letter following the first by less than a week, he failed to convince Kronecker of the legitimacy of his transfinite numbers. Cantor assumed that Kronecker had been preoccupied with the philosophical parts of the Grundlagen, thus overlooking the more concrete grounds upon which the transfinite numbers could be justified:

I am of the opinion that the greatest part of what I have done scientifically in the last few years, which I include under the rubric of set theory, is not so very much opposed to the demands which you place upon "concrete" mathematics as you seem to believe. It may be the fault of the presentation (which may not be entirely clear), that you have given less attention to the concrete mathematics in my research than to its other, namely, philosophical content.⁶⁰

Cantor realized that overcoming the breach with Kronecker was not really a question of persuasion but that only time would reveal the strength and rightness of his new work. During an evening's conversation at Kronecker's home in Berlin, early in October 1884, Cantor was further convinced that there was little hope in winning Kronecker away from the narrowness of his preconceptions. Cantor described the meeting, which ran into the early hours of the following morning, in a letter to Mittag-Leffler:

It seems to me of no small account that he and his preconceptions have been turned from the offensive to the defensive by the success of my work. As he told me, he wants to publish soon his opinions concerning arithmetic and the theory of functions. I wish it luck!⁶¹

The attempted though abortive reconciliation with Kronecker was but one of several events which were equally significant in contributing to Cantor's growing disillusionment with mathematics during the year following his first nervous breakdown. In the fall of 1884 he again took up the intricate problem of the continuum hypothesis. On August 26, 1884, little more than a week after his letter of reconciliation to Kronecker, Cantor had written to Mittag-Leffler announcing, at last, an extraordinarily simple proof that the continuum was equal in power to the second number class (II). The proof attempted to show that there were closed sets of the second power. Based upon straightforward decompositions and the fact that every perfect set was of power equal to that of the continuum, Cantor was certain that he had triumphed. He summarized the heart of his proposed proof in a single sentence: "Thus you see that everything comes down to defining a single closed set of the second power. When I've put it all in order, I will send you the details."⁶²

But on October 20 Cantor sent a lengthy letter to Mittag-Leffler followed three weeks later by another announcing the complete failure of the continuum hypothesis.⁶³ On November 14 he wrote saying he had found a rigorous proof that the continuum did not have the power of the second number class or of any number class. He consoled himself by saying that "the eventual elimination of so fatal an error, which one has held for so long, ought to be all the greater an advance."⁶⁴ Perhaps he was thinking back to the similar difficulties he had encountered in trying to decide whether or not the real numbers were denumerable, or how lines and planes might be corresponded. Cantor had come to learn that one should never be entirely surprised by the unexpected. Nevertheless, within twenty-four hours he had decided that his latest proof was wrong and that the continuum hypothesis was again an open question. It must have been embarrassing for him to have been compelled to reverse himself so often within such a short period of time in his correspondence with Mittag-Leffler. But even more discouraging must have been the realization that the simplicity of the continuum hypothesis concealed difficulties of a high order, ones that, despite all his efforts and increasingly sophisticated methods, he seemed no better able to resolve.

In attempting to find a solution for his continuum hypothesis, Cantor was led to introduce a number of new concepts enabling more sophisticated decompositions of point sets. These, he hoped, would eventually lead to a means of determining the power of the continuum. His attempt to publish these new methods and results marked the final and most devastating episode responsible for his disillusionment with mathematics and his discontent with colleagues both in Germany and abroad.

MITTAG-LEFFLER AND THE WITHDRAWAL OF CANTOR'S "PRINCIPIEN EINER THEORIE DER ORDNUNGSTYPEN" FROM PRESS

Early in 1885 Cantor chose to present a number of new ideas in two brief articles which were to be published in Acta Mathematica as letters to the editor and designated as "first" and "second" communications. The first of these, the

"Erste Mittheilung" of his "Principien einer Theorie der Ordnungstypen"⁶⁵ was set in type and dated February 21, 1885 (the mathematical significance of the Principien, as well as Cantor's innovation of order types, is discussed in Chapter 7). On February 25 he added another four paragraphs and sent these off as well. But to his dismay, on March 9, Mittag-Leffler wrote back suggesting that perhaps the "Erste Mittheilung" on order types should be withdrawn from press:

I am convinced that the publication of your new work, before you have been able to explain new positive results, will greatly damage your reputation among mathematicians. I know very well that basically this is all the same to you. But if your theory is once discredited in this way, it will be a long time before it will again command the attention of the mathematical world. It may well be that you and your theory will never be given the justice you deserve in our lifetime. Then the theory will be rediscovered in a hundred years or so by someone else, and then it will subsequently be found that you already had it all. Then, at least, you will be given justice. But in this way [by publishing the Principien], you will exercise no significant influence, which you naturally desire as does everyone who carries out scientific research.⁶⁶

Mittag-Leffler likened Cantor's work to Gauss' research on non-Euclidean geometry, saying that Gauss had always been reluctant to publish on the subject. He added that Cantor's work was no less revolutionary and needed to be treated with similar care. Mittag-Leffler's caution that few mathematicians were prepared for Cantor's new terminology and increasingly philosophical manner was probably genuine enough. But to Cantor it seemed that Mittag-Leffler was only concerned about the reputation of his journal. In recalling the event more than a decade later, he confided to Poincaré his real feelings:

Suddenly it was clear to me that he must wish to see my work withdrawn in the interests of his Acta Mathematica. The connection is as follows! Even my earlier work published since 1870 has not enjoyed the approval of the powers in Berlin: Weierstrass, Kummer, Borchardt, Kronecker. Had Mittag-Leffler ever published my theory of transfinite order types (which was even more audacious and went much further) in the Acta Mathematica, he would have endangered in the highest degree the existence of his undertaking, which is still very young and which depends principally upon the good will of the Berlin academics.⁶⁷

Cantor was deeply hurt by Mittag-Leffler's rejection of his latest research. More than his polemic with Kronecker, more than his nervous breakdown or the trouble he was having in finding a proof for his continuum hypothesis, Mittag-Leffler's suggestion that Cantor not print his new article in the Acta Mathematica was the most devastating. Though he never admitted that the incident affected his personal regard and friendship for Mittag-Leffler, thereafter he wrote less frequently and only seldom did he mention matters concerning his research. Cantor apparently believed that he had been abandoned by the last mathematician at all sympathetic with his struggle to establish the transfinite numbers. Consequently, he never published again in the pages of the Acta Mathematica.

Following this incident with Mittag-Leffler, Cantor was led to abandon mathematics almost entirely. Writing to the Italian mathematician Gerbaldi, he was candid about why he had decided to give up mathematics:

The real reasons why publication was interrupted then remains a mystery to me, and even today I do not know. I suddenly received a letter from M.L. [Mittag-Leffler] in which he wrote (to my great astonishment) that after serious consideration he regarded this publication as "about a hundred years too soon." Had M.L. had his way, I should have to wait until the year 1984, which to me seemed too great a demand!

Since I was therefore disgusted, as you will understand, with the mathematical journals, I began to publish my work in the Zeitschrift für Philosophie und philosophische Kritik. I did not decide until nine months ago to present the mathematical side of my theory once again in mathematical journals. But of course I never want to know anything again about Acta Mathematica.⁶⁸

By the end of 1885 Cantor was in many respects a disillusioned man. Largely but not entirely the result of Mittag-Leffler's suggestion that he not publish his article on order types, Cantor chose to renounce Acta Mathematica just as he had decided in 1878 never to publish again in Crelle's Journal. In both cases Cantor was piqued by what he considered to have been personal affronts, and in his characteristically hasty, even angry, way he would have no more to do with either journal. It was an unfortunate feature of his personality, but Cantor always took criticism of his work deeply and personally. Thus in turning his back on Acta Mathematica, it was inevitable that his friendship with Mittag-Leffler would suffer. Without Mittag-Leffler, whom Cantor regarded as one of the few professional sources of encouragement and understanding upon which he could rely, there seemed little reason to continue a frustrating battle against both German and foreign mathematicians. With little hope of advancing to a position in either Berlin or Göttingen, Cantor found his prospects as a mathematician hopelessly bleak, certainly demoralizing.

It was ironic that Schoenflies, in writing his account of Cantor's illness and several crises of 1884, could end by saying that he owed so much to Mittag-Leffler, "who was then his only friend to remain scientifically faithful, despite the many attempts to dissuade him."⁶⁹ In part what Schoenflies said was true. Mittag-Leffler had been one of the first mathematicians to use Cantor's work in establishing one of his own most important theorems. Mittag-Leffler had also been responsible for suggesting that Cantor's early work and parts of the Grundlagen be translated into French and thus be made available to a wide readership through the Acta Mathematica. Even so, one still must remember the consequences (though doubtless unintended) of Mittag-Leffler's suggestion that Cantor withdraw his paper on the theory of order types. Mittag-Leffler's suggestion came at an unfortunately critical moment in Cantor's life, at the end of a long and upsetting series of events which he must have felt himself powerless to control. His disenchantment with mathematics dates, not from his first serious breakdown nor from the escalating series of polemics with Kronecker, but from Mittag-Leffler's letter of March 1885. Until then, Cantor had continued to work on the continuum hypothesis. Even after his first nervous breakdown, he continued to make new and significant advances with his theory of order types. But in response to Mittag-Leffler's letter, Cantor immediately sent a telegram asking for the return of any of his manuscripts still in Mittag-Leffler's possession. Thereafter he apparently put his mathematics aside and began to devote more and more of his time to certain historical interests that were entirely nonmathematical, or to problems of philosophy and theology. Above all, he soon discovered among theologians of the Roman Catholic Church a level of interest and encouragement that he had never found among mathematicians.

However, before it is possible to evaluate the significance of these interests, and above all Cantor's lengthy and often detailed correspondence with Catholic intellectuals and theologians over his transfinite set theory, it is necessary to consider the new attitude toward science proclaimed by Pope Leo XIII in 1879. Above all, something must be said of the new climate of interest in scientific ideas, a climate greatly stimulated by Pope Leo's attempt to promote a revival of Thomistic philosophy as prescribed in his encyclical Aeterni Patris.

POPE LEO XIII AND THE ENCYCLICAL AETERNI PATRIS

Pope Leo XIII's attempt to reconcile the new and often perplexing discoveries of science with scripture and with the authorities of the Church encouraged a number of Catholic intellectuals to study the various branches of natural science in detail.⁷⁰ By virtue of one of his most influential encyclicals, Aeterni Patris, Leo XIII was to foster interest in scientific ideas generally and from one quarter at least to arouse interest in Cantor's mathematics in a very direct, if somewhat surprising, way.⁷¹

Gioacchino Pecci (1810-1903), later Pope Leo XIII, was given a classical education at the Jesuit school in Viterbo. After receiving the doctorate of theology from the Collegio Romano in 1832, he entered the Accademia dei Nobili in Rome. At the same time he studied both canon and civil law at the Sapienza University. Five years later he decided to enter the priesthood and was

ordained in December 1837. Following papal assignments in Naples and Perugia, he was appointed nuncio to Brussels by Pope Gregory XVI, who called Pecci back to Italy in 1844 to serve as the Archbishop of Perugia. Ten years later, in 1853, he was made a cardinal.

At this time Gioacchino's brother, Giuseppe Pecci, was also in Perugia serving as a Jesuit professor at the local seminary, and it was under his influence that Gioacchino became interested in Thomistic philosophy.⁷² He even founded an Academy of St. Thomas in 1859. As Archbishop of Perugia, in the years 1876-1877, Gioacchino Pecci issued an important series of pastoral letters devoted to matters of the Church and civilization, in which he argued that the Church had to enter the current of modern times or be left behind.⁷³ To Pecci science was one of the most immediate representatives of modernity. But his pastoral letters were only a presentiment of the papal encyclicals to follow.

In 1878, having been elected by the College of Cardinals to succeed Gregory XVI, Gioacchino Pecci took the name Pope Leo XIII. He was meant to be a transitional Pope, but his pontificate lasted for twenty-five years. Among the first of his pronouncements was the encyclical Aeterni Patris, delivered on August 4, 1879. Urged by his brother, by then Cardinal Giuseppe Pecci, Leo XIII sought a renewal of philosophical thought along the lines of a revived Thomism.⁷⁴ Seen as an opposing force to political and social liberalism, Leo XIII's new program included several attempts to revitalize and to modernize the thought of the Church by reorganizing the Academy of St. Thomas, and by nominating Désiré Mercier (later to become one of the most prominent figures of the neo-Thomist movement), to a chair of Thomism at the University of Louvain. In fact, the Institut Supérieur de Philosophie at Louvain was organized by Mercier under the auspices of the Pope himself.⁷⁵

The basic position of the neo-Thomists may be characterized succinctly, if somewhat oversimply, by their conviction that contemporary evils were the result of false philosophy. Improper or incorrect views of nature, they held, resulted in two consequences: atheism and materialism. Since the time of Thomas Hobbes, science had been repeatedly charged with having spawned these two undesirable offspring, but rarely was science then called upon to fill the gap and to rebuke these dreaded Leviathans on their own grounds. The encyclical Aeterni Patris was clear on one point in particular: that science could profit from scholastic philosophy and in the process could further the ideals and goals of the Church itself:

For, the investigation of facts and the contemplation of nature is not alone sufficient for their profitable exercise and advance; but, when facts have been established, it is necessary to rise and apply ourselves to the study of the nature of corporeal things, to inquire into the laws which govern them and the principles whence their order and varied unity and mutual attraction in diversity arise. To such investigations it is wonderful what force and light and aid the Scholastic philosophy, if judiciously taught, would bring.⁷⁶

In dealing with the metaphysics of science, neo-Thomism was expected to guide the human understanding of the natural and spiritual world in the proper and unobjectionable direction prescribed by the Church, specifically along the lines defined implicitly in the encyclical Aeterni Patris. But the program which Leo XIII envisioned was less a subordination of philosophy and Thomistic teachings to science than an attempt to show how science ought to proceed and how it ought to be reconciled with the true principles of Christian philosophy. On April 21, 1878, in his first papal encyclical Inscrutabili, Leo wrote:

Above all [education] must be wholly in harmony with the Catholic faith in its literature and system of training, and chiefly in philosophy, upon which the foundation of other sciences in great measure depends.⁷⁷

But there was opposition to Leo XIII's efforts to commend the study of St. Thomas as the epitome of true philosophy. In fact, there was strong resistance among the clergy in Rome. As a result, it was suggested that a free course on Thomism should be established; and thus Father Giovanni Cornoldi (1822-1892), a Jesuit with a high reputation as both a scientist and a philosopher, was imported from Bologna to establish Thomism in the papal city.⁷⁸ Cornoldi went so far as to promise that "in the Summa Theologica was to be found the key to all the difficulties of modern science."⁷⁹ In stressing the harmony between Thomism and science, Cornoldi paved the way for renewed interest among churchmen in the affairs of science. Shortly after Cornoldi had begun his lectures in Rome, the encyclical Aeterni Patris was issued.

The impetus Leo XIII gave to scholarly and scientific study among intellectuals of the Church cannot be overestimated. Of special significance was the interest his encyclical generated among Germans who were to become interested in reconciling Cantor's work on absolute infinities with doctrines of Catholicism. Of particular importance in this respect was Constantin Gutberlet.

GUTBERLET AND THE APPRECIATION OF CANTOR'S WORK IN GERMANY

Constantin Gutberlet studied philosophy and theology at the Collegio Romano from 1856 to 1862, attending simultaneously the German University in Rome.⁸⁰ From 1862 to 1865 he lectured on the natural sciences at the seminary in Fulda, where he was made a professor of philosophy, apologetics, and dogma in 1866. In 1888 he founded the review journal, Philosophisches Jahrbuch der Görres-Gesellschaft, which proved to be a leading advocate of neo-Scholastic thought. But of special interest here was an article he published in 1886 drawing upon Cantor's set theory in a defense of his own views on the theological and philosophical nature of the infinite.⁸¹

Gutberlet realized that the study of infinity had entered a new phase with the appearance of Cantor's mathematical and philosophical studies. The question uppermost in Gutberlet's mind concerned the challenge of mathematical infinity to the unique, absolute infinity of God's existence. It was not long before correspondence over this question began to deepen Cantor's interest in the theological aspects of his theory of the transfinite numbers. It was Cantor's claim that instead of diminishing the extent of God's nature and dominion, the transfinite numbers actually made it all the greater.⁸²

It is not important to follow the details of Gutberlet's article. It is important to know only that it was, in its broadest outline, an attempt to support arguments he had advanced several years earlier on the existence of the actual infinite. Subsequently, Gutberlet's ideas had been attacked in severe terms by another German, Caspar Isenkrahe.⁸³ Isenkrahe argued that the actual infinite was self-contradictory, and thus any attempts to support it were necessarily hopeless. The discussion was couched in terms of the infinite duration and eternity of the world, and it raised objections to theories of actual infinities made by thinkers as diverse in time as Aquinas and Herbart.⁸⁴ Gutberlet presented Cantor's work to support his own claims against opposition from theologians like Isenkrahe. By describing Cantor's mathematics, Gutberlet hoped that any reader could then decide:

if they were correct, when they supposed they could dispose of my theory of actually infinite magnitude [Grösse] so easily. Above all we [Gutberlet] now want to explain the Cantorian theory and then to defend our conception against criticism, which this journal published with Cantor's corresponding interpretation of infinite magnitude.⁸⁵

The use which Gutberlet made of Cantor's ideas is of some interest. Particularly when it came to defending the existence of the absolute infinite, Gutberlet used a ploy reminiscent of Berkeley's use of God as a guarantor of the reality of the external world. In short, Gutberlet argued that God Himself ensured the existence of Cantor's transfinite numbers:

But in the absolute mind the entire sequence is always in actual consciousness, without any possibility of increase in the knowledge or contemplation of a new member of the sequence.⁸⁶

God was similarly called upon to ensure the ideal existence of infinite decimals, the irrational numbers, the true and exact value of p, and so on. God was not only capable of resolving the problem of the continuum hypothesis, but he also ensured the concreteness and objectivity of the cardinal number representing the collection of all real numbers.⁸⁷ Gutberlet even argued that, since the mind of God was believed to be unchanging, then the collection of divine thoughts must comprise an absolute, infinite, complete, closed set. Again, Gutberlet offered this as direct evidence for the reality of concepts like Cantor's transfinite numbers. Either one assumed the existence and reality of the actual infinite, or one was obliged to give up the infinite intellect and eternity of the absolute mind of God.

Gutberlet thus called upon Cantor's analysis of the infinite to defend his own use of actually infinite numbers. In the process he encouraged Cantor's interest in the philosophical and theological aspects of his work. That Gutberlet was prepared to argue the objective possibility of the transfinite numbers on the basis of the infinite intellect of God must have appealed to the mind of a religious man like Cantor.⁸⁸ It was also a complementary approach to Cantor's own Platonism, in which the legitimacy of the actual infinite was established in the immanent world of the mind by virtue of the consistent forms of reason alone.⁸⁹

INFINITY, PANTHEISM, AND NEO-THOMIST RESPONSE TO TRANSFINITE SET THEORY

Though Gutberlet was one of Germany's leading neo-Thomists,⁹⁰ he was by no means the only philosopher of the Catholic Church who was interested in Cantor's mathematics. Cantor counted among his correspondents Tillman Pesch, Thomas Esser, Joseph Hontheim, and Ignatius Jeiler. All of these were closely involved with the revival of scholastic philosophy in the spirit of Aeterni Partis. Pesch⁹¹ and Hontheim⁹² were associated with a group of Jesuits at the Abbey of Maria-Laach, (on Lake Laach, near Andemach in the Rheinland, Germany), where a series of important contributions to neo-Thomism were published under the title Philosophia Lacensis. Pesch, in a work which attempted to describe the foundations of a Thomistic cosmology, the Institutiones Philosophiae Naturalis, was chiefly concerned with the progress of science in the nineteenth century.⁹³ Hontheim, writing for the same series, published a work on mathematics and logic in 1895: Der logische Algorithmus. Jeiler was a prominent figure among another group of neo-Thomists at Quaracchi, near Florence, and at Leo XIII's commission, he undertook a new edition of the works of St. Bonaventura in direct response to Leo's encyclical Aeterni Patris.⁹⁴

Equally representative of the Church's interest in Cantor's mathematics was Thomas Esser, a Dominican in Rome. Apparently, Esser represented a group of Dominicans who were engaged in careful study of the theological implications of Cantor's work. In 1896 Cantor described their project in a letter to Jeiler:

Now everything concerning this question (I tell you this in confidence) will of course be examined by the Dominicans in Rome, who are conducting a scholarly [wissenschaftliche] correspondence with me about it [BAD TEXT] will be directed by Father Thomas Esser, O. Pr.⁹⁵

An important concern of the Catholic intellectuals who knew of Cantor's work involved the question of whether the transfinite numbers could be said to exist in concreto. Gutberlet was always clear that he differed fundamentally with Cantor on the matter, admitting the actual infinite as a "possible," and even real in the immanent, nonphysical dimensions of God's mind.⁹⁶ But Gutberlet, like his teacher Cardinal Franzelin, denied the possibility of a concrete, objective Transfinitum for reasons that make the Church's concern for Cantor's work understandable.

Cardinal Johannes Franzelin (1816-1886) was a leading Jesuit philosopher and papal theologian to the Vatican Council, the twentieth ecumenical council (1869-1870) called by Pope Pius IX, and famous for its promulgation of the dogma of papal infallability.⁹⁷ Cardinal Franzelin responded to Cantor's belief that the Transfinitum existed in natura naturata by explaining that it was a dangerous position to hold. Franzelin held that any belief in a concrete Transfinitum "could not be defended and in a certain sense would involve the error of Pantheism."⁹⁸ Pantheism, of course, had long been anathema to the Christian Church but was not condemned formally until 1861 by decree of Pius IX.⁹⁹ Spinoza, a philosopher Cantor had studied carefully, used the natura naturans/natura naturata distinction in a form similar to that of his heretical forerunner Giordano Bruno.¹⁰⁰ Both had been led to advocate a monistic philosophy of substance identifying God with the natural world. The question of the infinite was an easy touchstone identifying pantheistic doctrines. Any attempt to correlate God's infinity with a concrete, temporal infinity suggested Pantheism. Thus infinite space and infinite duration were both instances where the infinite, predicated of objects in the natural world, were held to be inadmissible on theological grounds. Any actual infinite in concreto, in natura naturata, was presumably identifiable with God's infinity, in natura naturans. Cantor, by arguing his actually infinite transfinite numbers in concreto, seemed to some to be aiding the cause of Pantheism.

These were the grounds upon which Gutberlet and Franzelin had been led to object to the admissibility of the actual, concrete infinite as more than a "possible" infinite. Cantor however, believing in the "actual," concrete infinite, was able to add a distinction between two sorts in infinity that was to satisfy at least some theologians, and in particular Cardinal Franzelin. On January 22, 1886, Cantor wrote to the cardinal explaining that in addition to differentiating between the infinite in natura naturans and in natura naturata, he further distinguished between an "Infinitum aeternum increatum sive Absolutum," reserved for God and his attributes, and an "Infinitum creatum sive Transfinitum," evidenced throughout created nature and exemplified in the actually infinite number of objects in the universe.¹⁰¹ Cantor added that the important difference between absolute infinitum and actual transfinitum should not be forgotten. Cantor's clarifications turned Franzelin's reluctance into an imprimatur of sorts, when Franzelin chose to endorse Cantor's distinctions as follows:

Thus the two concepts of the Absolute-Infinite and the Actual-Infinite in the created world or in the Transfinitum are essentially different, so that in comparing the two one must only describe the former as properly infinite, the latter as improperly and equivocally infinite. When conceived in this way, so far as I can see at present, there is no danger to religious truths in your concept of the Transfinitum.¹⁰²

Cantor was always proud of the acceptance his new theory had found in the estimation of Cardinal Franzelin and would frequently remind his friends in the Church, through correspondence, that he had been assured on the cardinal's authority that the theory of transfinite numbers posed no theological threats to religion.¹⁰³ In fact, Cantor believed that the real existence of the Transfinitum further reflected the infinite nature of God's existence. Cantor even devised a pair of arguments from which the existence of transfinite numbers in concreto could be deduced on both a priori and a posteriori grounds. A priori, the concept of God led directly on the basis of the perfection of His being to the possibility and necessity of the creation of a Transfinitum.¹⁰⁴ Approaching the same conclusion with a posteriori arguments, Cantor believed that the assumption of a Transfinitum in natura naturata followed because the complete explanation of natural phenomena was impossible on exclusively finite assumptions.¹⁰⁵ Either way, Cantor felt he had demonstrated the necessity of accepting the Transfinitum in concreto, and he was not reluctant to call upon the nature and attributes of God in order to do so.

CHRISTIAN PHILOSOPHY AND ITS IMPORTANCE FOR CANTORIAN SET THEORY

The interest generated by Leo XIII's encyclical Aeterni Patris was a tonic for Cantor's own declining spirits. Following his nervous breakdown in the late spring of 1884, Cantor returned to mathematics only to be doubly discouraged. Not only was the continuum hypothesis a hopeless tangle, but early in 1885, Mittag-Leffler seemed to have closed the last door on Cantor's hopes for encouragement and understanding among mathematicians. Isolated in Halle, Cantor began to teach philosophy and to correspond with theologians who provided a natural outlet for Cantor's need to communicate the importance and implications of his work.¹⁰⁶

In turn, Cantor's contact with Catholic theologians may have made his own religious sympathies all the stronger. By the early part of 1884, he could write to Mittag-Leffler that he was not the creator of his new work, but merely a reporter. God had provided the inspiration, leaving Cantor responsible only for the way in which his articles were written, for their style and organization, but not for their content.¹⁰⁷ Apparently hoping to disassociate himself as much as possible from having to assume responsibility for his controversial research, Cantor was trying to shield himself from the criticism his transfinite numbers were destined to generate. Psychologically, the letter to Mittag-Leffler is revealing because it clearly demonstrates that before his first nervous breakdown, he was no longer anxious to take credit for his work but was willing to place the burden of responsibility for the provocative new ideas elsewhere.

It is also significant that Cantor believed in the absolute truth of his set theory because it had been revealed to him. Thus he may have seen himself not only as God's messenger, accurately recording, reporting, and transmitting the newly revealed theory of the transfinite numbers but as God's ambassador as well. If so, Cantor would not only have felt it appropriate, but more accurately, his duty, to use the knowledge which was his by the grace of God to prevent the Church from committing any grave errors with respect to doctrines concerning the nature of infinity. In writing to Jeiler during Whitsuntide 1888, Cantor declared:

I entertain no doubts as to the truth of the transfinites, which I have recognized with God's help and which, in their diversity, I have studied for more than twenty years; every year, and almost every day brings me further in this science.¹⁰⁸

Cantor was even more direct in a letter written to Hermite during the first month of 1894, in which he claimed that it was God's doing that led him away from serious mathematics to concerns of theology and philosophy:

But now I thank God, the all-wise and all-good, that He always denied me the fulfillment of this wish [for a position at university in either Göttingen or Berlin], for He thereby constrained me, through a deeper penetration into theology, to serve Him and His Holy Roman Catholic Church better than I have been able with my exclusive preoccupation with mathematics.¹⁰⁹

At one stroke, Cantor signaled the many disappointments and doubts accumulated over more than two decades. His lack of confidence in himself and his mathematical powers reflected the frustration he must have felt at being unable to solve the continuum hypothesis, compounded by the disastrous effects of Kronecker's attacks and of Mittag-Leffler's seemingly negative response to his recent work on order types. Realizing that no positions were ever going to be offered him in either Göttingen or Berlin,¹¹⁰ Cantor turned to other interests less demanding than his mathematics, and more positively reinforcing. Later he interpreted his disaffection from mathematics and his deepening interest in philosophy and theology as the work of God. By the end of his life, in the spirit of Aeterni Patris, Cantor saw himself as the servant of God, a messenger or reporter who could use the mathematics he had been given to serve the Church. As he told Esser in early February 1896: "From me, Christian Philosophy will be offered for the first time the true theory of the infinite."¹¹¹

Cantor had given up his mathematical colleagues and had found both consolation and inspiration among theologians and philosophers of the Church. Religion renewed his confidence and sustained his belief in the truth and significance of his research. Inspired and helped by God, Cantor was sure that his work was of consequence, despite the failure of mathematicians to understand the importance of his discoveries.