The symbol for infinity that one sees most often is the lazy eight curve, technically called the lemniscate. This symbol was first used in a seventeenth century treatise on conic sections.¹ It caught on quickly and was soon used to symbolize infinity or eternity in a variety of contexts. For instance, in the 1700s the infinity symbol began appearing on the Tarot card known as the Juggler or the Magus. It is an interesting coincidence that the Qabbalistic symbol associated with this particular Tarot card is the Hebrew letter À (pronounced alef), for Georg Cantor, the founder of the modern mathematical theory of the infinite, used the symbol À₀ (pronounced alef-null) to stand for the first infinite number.

The appropriateness of the symbol 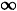for infinity lies in the fact that one can travel endlessly around such a curve ... demolition derby style, if you will. Endlessness is, after all, a principal component of one's concept of infinity. Other notions associated with infinity are indefiniteness and inconceivability.

Infinity commonly inspires feelings of awe, futility, and fear. Who as a child did not lie in bed filled with a slowly mounting terror while sinking into the idea of a universe that goes on and on, for ever and ever? Blaise Pascal puts this feeling very well: "When I consider the small span of my life absorbed in the eternity of all time, or the small part of space which I can touch or see engulfed by the infinite immensity of spaces that I know not and that know me not, I am frightened and astonished to see myself here instead of there ... now instead of then."²

It is possible to regard the history of the foundations of mathematics as a progressive enlarging of the mathematical universe to include more and more infinities. The Greek word for infinity was apeiron, which literally means unbounded, but can also mean infinite, indefinite, or undefined. Apeiron was a negative, even pejorative, word. The original chaos out of which the world was formed was apeiron. An arbitrary crooked line was apeiron. A dirty crumpled handkerchief was apeiron. Thus, apeiron need not only mean infinitely large, but can also mean totally disordered, infinitely complex, subject to no finite determination. In Aristotle's words, "... being infinite is a privation, not a perfection but the absence of a limit..."³

There was no place for the apeiron in the universe of Pythagoras and Plato. Pythagoras believed that any given aspect of the world could be represented by a finite arrangement of natural numbers (where "natural number" means "whole number"). Plato believed that even his ultimate form, the Good, must be finite and definite. This was in contradistinction to almost all later metaphysicians, who assumed that the Absolute is necessarily infinite. In the next chapter I will discuss the way in which Greek mathematics was limited by this refusal to accept the apeiron, even in the relatively harmless guise of a real number with an infinite decimal expansion.

Aristotle recognized that there are many aspects of the world that seem to point to the actuality of the apeiron. For instance, it seems possible that time will go on forever; and it would seem that space is infinitely divisible, so that any line segment contains an infinity of points. In order to avoid these actual infinites that seemed to threaten the orderliness of his a priori finite world, Aristotle invented the notion of the potentially infinite as opposed to the actually infinite. I will describe this distinction in more detail in the next section, but for now let me characterize it as follows. Aristotle would say that the set of natural numbers is potentially infinite, since there is no largest natural number, but he would deny that the set is actually infinite, since it does not exist as one finished thing. This is a doubtful distinction, and I am inclined to agree with Cantor's opinion that "... in truth the potentially infinite has only a borrowed reality, insofar as a potentially infinite concept always points towards a logically prior actually infinite concept whose existence it depends on."⁴

Plotinus was the first thinker after Plato to adopt the belief that at least God, or the One, is infinite, stating of the One that, "Absolutely One, it has never known measure and stands outside of number, and so is under no limit either in regard to anything external or internal; for any such determination would bring something of the dual into it."⁵

St. Augustine, who adapted the Platonic philosophy to the Christian religion, believed not only that God was infinite, but also that God could think infinite thoughts. St. Augustine argued that, "Such as say that things infinite are past God's knowledge may just as well leap headlong into this pit of impiety, and say that God knows not all numbers. . . . What madman would say so? . . . What are we mean wretches that dare presume to limit His knowledge?"⁶

This extremely modern position will be returned to in the last section of this chapter. Later medieval thinkers did not go as far as Augustine and, although granting the unlimitedness of God, were unwilling to grant that any of God's creatures could be infinite. In his Summa Theologiae St. Thomas Aquinas gives a sort of Aristotelian proof that "although God's power is unlimited, he still cannot make an absolutely unlimited thing, no more than he can make an unmade thing (for this involves contradictories being true together)."⁷ The arguments are elegant, but suffer from the flaw of being circular: it is proved that the notion of an unlimited thing is contradictory by slipping in the premise that a "thing" is by its very nature limited.

Thus, with the exception of Augustine and a few others, the medieval thinkers were not prepared to deal with the infinitude of any entities other than God, be they physical, psychological, or purely abstract. The famous puzzle of how many angels can dance on the head of a pin can be viewed as a question about the relationship between the infinite Creator and the finite world. The crux of this problem is that, on the one hand, it would seem that since God is infinitely powerful, he should be able to bid an infinite number of angels to dance on the head of a pin; on the other hand, it was believed by the medieval thinkers that no actually infinite collection could ever arise in the created world.

Their proofs that infinity is somehow a self-contradictory notion were all flawed, but there was at least one interesting paradox involving infinity that the medieval thinkers were aware of. It would seem that any line includes infinitely many points. Since the circumference of a circle with radius two is two times as long as the circumference of a circle with radius one, then the former should include a larger infinity of points than the latter. But by drawing radii we can see that each point P on the small circle corresponds to exactly one point P' on the large circle, and each point Q' on the large circle corresponds to exactly one point Q on the small circle. Thus we seem to have two infinities that are simultaneously different and equal.

In the early 1600s Galileo Galilei offered a curious solution to this problem. Galileo proposed that the smaller length could be turned into the longer length by adding an infinite number of infinitely small gaps. He was well aware that such a procedure leads to various difficulties: "These difficulties are real; and they are not the only ones. But let us remember that we are dealing with infinites and indivisibles, both of which transcend our finite understanding, the former on account of their magnitude, the latter because of their smallness. In spite of this, men cannot refrain from discussing them, even though it must be done in a roundabout way."⁸

He resolved some of his difficulties by asserting that problems arise only "when we attempt, with our finite minds, to discuss the infinite, assigning to it those properties which we give to the finite and limited; but this I think is wrong, for we cannot speak of infinite quantities as being the one greater or less than or equal to another."⁹ This last assertion is supported by an example that is sometimes called Galileo's paradox.

The paradoxical situation arises because, on the one hand, it seems evident that most natural numbers are not perfect squares, so that the set of perfect squares is smaller than the set of all natural numbers; but, on the other hand, since every natural number is the square root of exactly one perfect square, it would seem that there are just as many perfect squares as natural numbers. For Galileo the upshot of this paradox was that, "we can only infer that the totality of all numbers is infinite, and that the number of squares is infinite . . .; neither is the number of squares less than the totality of all numbers, nor the latter greater than the former; and finally, the attributes 'equal,' 'greater,' and 'less,' are not applicable to infinite, but only to finite quantities."¹⁰

I have quoted Galileo at some length, because it is with him that we have the first signs of the modern attitude toward the actual infinite in mathematics. If infinite sets do not behave like finite sets, this does not mean that infinite is an inconsistent notion. It means, rather, that infinite numbers obey a different "arithmetic" from finite numbers. If using the ordinary notions of "equal" and "less than" on infinite sets leads to contradictions, this is not a sign that infinite sets cannot exist, but, rather, that these notions do not apply without modification to infinite sets. Galileo himself did not see how to carry out such a modification of these notions; this was to be the task of Georg Cantor, some 250 years later.

One of the reasons that Galileo felt it necessary to come to some sort of terms with the actual infinite was his desire to treat space and time as continuously varying quantities. Thus, the results of an experiment on motion can be stated in the form that x = f(t), that space position is a certain function of continuously changing time. But this variable t that grows continuously from, say, zero to ten is apeiron, both in the sense that it takes on arbitrary values, and in the sense that it takes on infinitely many values.

This view of position as a function of time introduced a problem that helped lead to the founding of the Calculus in the late 1600s. The problem was that of finding the instantaneous velocity of a moving body, whose distance x from its starting point is given as a function f(t) of time.

It turns out that to calculate the velocity at some instant t_o, one has to imagine measuring the speed over an infinitely small time interval dt. The speed f'(t_o) at t_o is given by the formula (f(t_o + dt) - f(t_o))/dt, as everyone who has ever survived a first-year calculus course knows.

The quantity dt is called an infinitesimal, and obeys many strange rules. If dt is added to a regular number, then it can be ignored, treated like zero. But, on the other hand, dt is regarded as being different enough from zero to be usable as the denominator of a fraction. So is dt zero or not? Adding finitely many infinitesimals together just gives another infinitesimal. But adding infinitely many of them together can give either an ordinary number, or an infinitely large quantity.

Bishop Berkeley found it curious that mathematicians could swallow the Newton-Leibniz theory of infinitesimals, yet balk at the peculiarities of orthodox Christian doctrine. He wrote about this in a 1734 work, the full title of which was, The Analyst, Or A Discourse Addressed to an Infidel Mathematician. Wherein It is examined whether the Object, Principles, and Inferences of the modern Analysis are more distinctly conceived, or more evidently deduced, than Religious Mysteries and Points of Faith. "First cast out the beam out of thine own Eye; and then shalt thou see clearly to cast out the mote out of thy brother's Eye." ¹¹

The use of infinitely small and infinitely large numbers in calculus was soon replaced by the limit process. But it is unlikely that the Calculus could ever have developed so rapidly if mathematicians had not been willing to think in terms of actual infinities. In the past fifteen years, Abraham Robinson's non-standard analysis has produced a technique by which infinitesimals can be used without fear of contradiction. Robinson's technique involves enlarging the real numbers to the set of hyperreal numbers, which will be discussed in Chapter 2.

After the introduction of the limit process, calculus was able to advance for a long time without the use of any actually infinite quantities. But as mathematicians tried to get a precise description of the continuum or real line, it became evident that infinities in the foundations of mathematics could only be avoided at the cost of great artificiality. Mathematicians, however, still hesitated to plunge into the world of the actually infinite, where a set could be the same size as a subset, a line could have as many points as a line half as long, and endless processes were treated as finished things.

It was George Cantor who, in the late 1800s, finally created a theory of the actual infinite which by its apparent consistency, demolished the Aristotelian and scholastic "proofs" that no such theory could be found. Although Cantor was a thoroughgoing scholar who later wrote some very interesting philosophical defenses of the actual infinite, his point of entry was a mathematical problem having to do with the uniqueness of the representation of a function as a trigonometric series.

To give the flavor of the type of construction Cantor was working with, let us consider the construction of the Koch curve shown in Figure 4. The Koch curve is found as the limit of an infinite sequence of approximations. The first approximation is a straight line segment (stage 0). The middle third of this segment is then replaced by two pieces, each as long as the middle third, which are joined like two sides of an equilateral triangle (stage 1). At each succeeding stage, each line segment has its middle third replaced by a spike resembling an equilateral triangle.

Now, if we take infinity as something that can, in some sense, be attained, then we will regard the limit of this infinite process as being a curve actually existing, if not in physical space, then at least as a mathematical object. The Koch curve is discussed at length in Benoit Mandelbrot's book, Fractals, where he explains why there is reason to think of the Koch curve in its infinite spikiness as being a better model of a coastline than any of its finitely spiky approximations.¹²

Cantor soon obtained a number of interesting results about actually infinite sets, most notably the result that the set of points on the real line constitutes a higher infinity than the set of all natural numbers. That is, Cantor was able to show that infinity is not an all or nothing concept: there are degrees of infinity.

This fact runs counter to the naive concept of infinity: there is only one infinity, and this infinity is unattainable and not quite real. Cantor keeps this naive infinity, which he calls the Absolute Infinite, but he allows for many intermediate levels between the finite and the Absolute Infinite. These intermediate stages correspond to his transfinite numbers . . . numbers that are infinite, but none the less conceivable.

In the next section we will discuss the possibility of finding physically existing transfinite sets. We will then look for ways in which such actual infinities might exist mentally. Finally we will discuss the Absolute, or metaphysical, infinite.

This threefold division is due to Cantor, who, in the following passage, distinguishes between the Absolute Infinite, the physical infinities, and the mathematical infinities:

The actual infinite arises in three contexts: first when it is realized in the most complete form, in a fully independent other-worldly being, in Deo, where I call it the Absolute Infinite or simply Absolute; second when it occurs in the contingent, created world; third when the mind grasps it in abstracto as a mathematical magnitude, number, or order type. I wish to make a sharp contrast between the Absolute and what I call the Transfinite, that is, the actual infinities of the last two sorts, which are clearly limited, subject to further increase, and thus related to the finite.¹³

PHYSICAL INFINITIES¹⁴

There are three ways in which our world appears to be unbounded and thus, perhaps, infinite. It seems that time cannot end. It seems that space cannot end. And it seems that any interval of space or time can be divided and subdivided endlessly. We will consider these three apparent physical infinities in three subsections.

Temporal Infinities

Suppose that the human race was never going to die out -- that any given generation would be followed by another generation. Would we not then have to admit that the number of generations of man is actually infinite?

Aristotle argued against this conclusion, asserting that in this situation the number of generations of man would be but potentially infinite; that is, infinite only in the sense of being inexhaustible. He maintained that at any given time there would only have been some finite number of generations, and that it was not permissible to take the entire future as a single whole containing an actual infinitude of generations.

It is my opinion that this sort of distinction rests on a view of time that has been fairly well discredited by modern relativistic physics. In order to agree with Aristotle that, although there will never be a last generation, there is no infinite set of all the generations, we must believe that the future does not exist as a stable, definite thing. For if we have the future existing in a fixed way, then we have all of the infinitely many future generations existing "at once."

But one of the chief consequences of Einstein's Special Theory of Relativity is that it is space-time that is fundamental, not isolated space which evolves as time passes. I will not argue this point in detail here, but let me repeat that on the basis of modern physical theory we have every reason to think of the passage of time as an illusion. Past, present, and future all exist together in space-time.

So the question of the infinitude of time is not one that is to be dodged by denying that time can be treated as a fixed dimension such as space. The question still remains: is time infinite? If we take the entire space-time of our universe, is the time dimension infinitely extended or not?

Fifty, or even twenty, years ago it would have been natural to assert that our universe has no beginning or end and that time is thus infinite in both directions. But recently it has become an established fact that the universe does have a beginning in time known as the Big Bang. The Big Bang took place approximately 15 billion years ago. At that time our universe was the size of a point, and it has been expanding ever since. What happened before the Big Bang? It is at least possible to answer, "Nothing." The apparent paradox of having a first instant in time is sometimes avoided by saying that the Big Bang did not occur in time . . . that time is open, rather than closed, in the past.

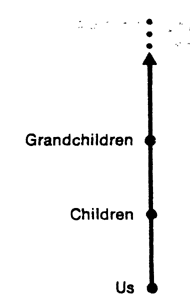
This is a subtle distinction, but a useful one. If we think of time as being all the points greater than or equal to zero, then there is a first instant: zero. But if we think of time as being all the points strictly greater than zero, then there is no first instant. For any instant t greater than zero, one has an earlier instant t/2 that is also greater than zero.

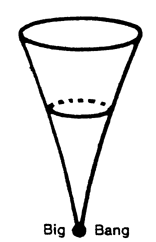
But in any case, if we think of time as not existing before the Big Bang, then there are certainly not an infinite number of years in our past. And what about the future? There is no real consensus on this. Many cosmologists feel that our universe will eventually stop expanding and collapse to form a single huge black hole called the Big Stop or the Gnab Gib; others feel that the expansion of the universe will continue indefinitely.

If the universe really does start as a point and eventually contract back to a point, is it really reasonable to say that there is no time except for the interval between these points? What comes before the beginning and after the end?

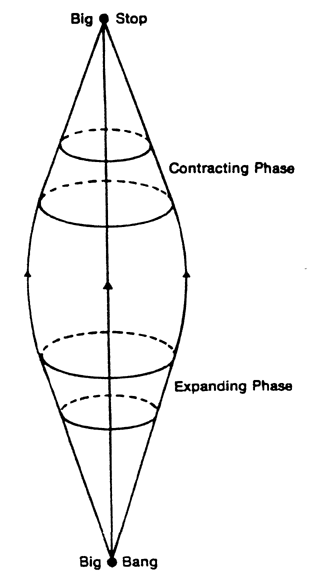
One response is to view the universe as an oscillating system, which repeatedly goes through expansions and contractions. This would reintroduce an infinite time, which could, however, be avoided.

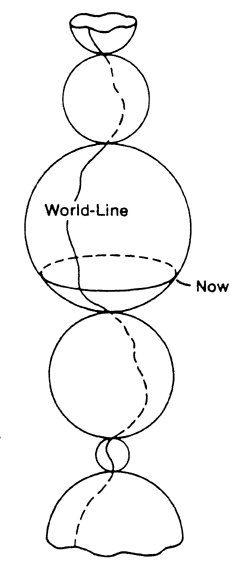
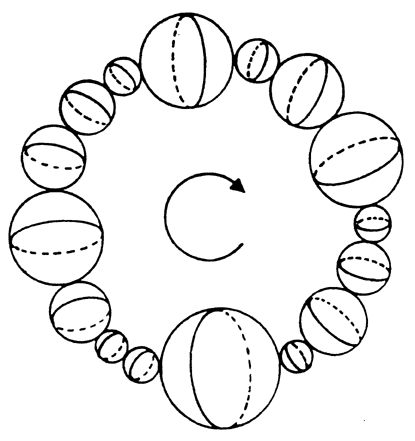
The way in which one would avoid infinite time in an endlessly oscillating universe would be to adopt a belief in what used to be called "the eternal return." This is the belief that every so often the universe must repeat itself. The idea is that a finite universe must return to the same state every so often, and that once the same state has arisen, the future evolution of the universe will be the same as the one already undergone. The doctrine of eternal recurrence amounts to the assumption that Figure 11. From R. v.B. Rucker, Geometry, Relativity, and the Fourth Dimension.

time is a vast circle. An oscillating universe with circular time is pictured in Figure 10.

There is a simpler model of an oscillating universe with circular time, which can be called toroidal space-time. In toroidal space-time we have an oscillating universe that repeats itself after every cycle. Such a model is obtainable by identifying the two points, "Big Bang" and "Big Stop," in Figure 11.

Note, however, that if the universe really expands forever, then it cannot ever repeat itself, as the average distance between galaxies is a continually increasing quantity that never returns to the same value.

Spatial Infinities

We now turn to a consideration of the possibility of spatial infinities. The potential versus actual infinity distinction is sometimes used to try to scotch this question at the outset. Immanuel Kant, for instance, argues that the world cannot be an infinite whole of coexisting things because "in order therefore to conceive the world, which fills all space, as a whole, the successive synthesis of the parts of an infinite world would have to be looked upon as completed; that is, an infinite time would have to be looked upon as elapsed, during the enumeration of all coexisting things."¹⁵

Kant's point is that space is in some sense not already really there -- that things exist together in space only when a mind perceives them to do so. If we accept this, then it is true that an infinite space is something that no finite mind can know of after any finite amount of time. But one feels that the world does exist as a whole, in advance of any efforts on our part to see it as a unity. And if we take all of space-time, it certainly does not seem to be meaningless to ask whether the spatial extent of space-time is infinite or not.

In De Rerum Natura, Lucretius first gave the classic argument for the unboundedness of space: "Suppose for a moment that the whole of space were bounded and that someone made his way to its uttermost boundary and threw a flying dart."¹⁶ It seems that either the dart must go past the boundary, in which case it is no boundary of space; or the dart must stop, in which case there is something just beyond the boundary that stops it, which again means that the purported boundary is not really the end of the universe.

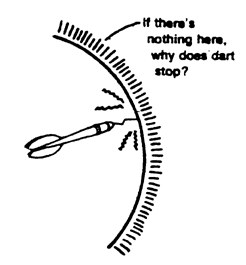
So great was their revulsion against the apeiron that Parmenides, Plato, and Aristotle all held that the space of our universe is bounded and finite, having the form of a vast sphere. When faced with the question of what lies outside this sphere, Aristotle maintained that "what is limited, is not limited in reference to something that surrounds it."¹⁷

In modern times we have actually developed a way to make Aristotle's claim a bit more reasonable. As Lucretius realized, the weak point in the claim that space is a finite sphere is that such a space has a definite boundary. But there is a way to construct a three-dimensional space which is finite and which does not have boundary points: simply take the hypersurface of a hypersphere. Such a space is endless but not infinite.

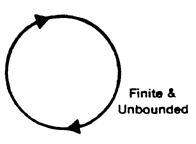
To understand how something can be endless but not infinite, think of a circle. A fly can walk around and around the rim of a glass without ever coming to a barrier or stopping point, but none the less he will soon retrace his steps.

Again, the surface of the Earth is a two-dimensional manifold which is finite but unbounded (unbounded in the sense of having no edges). You can travel and travel on the Earth's surface without ever coming to any truly impassible barrier . . . but if you continue long enough, you will begin to recross your steps.

The reason that the two-dimensional surface of the Earth is finite but unbounded is that it is bent, in three-dimensional space, into the shape of a sphere. In the same way, it is possible to imagine the three-dimensional space of our universe as being bent, in some four-dimensional space, into the shape of a hypersphere. It was Bernhard Riemann who first realized this possibility in 1854. There is, however, a traditional belief that anticipates the hypersphere. This tradition, described in the essay, "The Fearful Sphere of Pascal," by Jorge Luis Borges, is summarized by the saying (attributed to the legendary magician Hermes Trismegistus) that "God is an intelligible sphere, whose center is everywhere and whose circumference is nowhere."¹⁸ If the universe is indeed a hypersphere, then it would be quite accurate to regard it as a sphere whose center is everywhere and whose circumference is nowhere.

To see why this is so, consider the fact that if space is hyperspherical, then one can cover all of space by starting at any point and letting a sphere expand outwards from that point. The curious thing is that if one lets a sphere expand in a hyperspherical space, there comes a time when the circumference of the sphere turns into a point and disappears. This fact can be grasped by considering the analogous situation of the sequence of circular latitude lines on the spherical surface of the earth.¹⁹ This line of thought appears in Dante's Paradisio (1300).²⁰

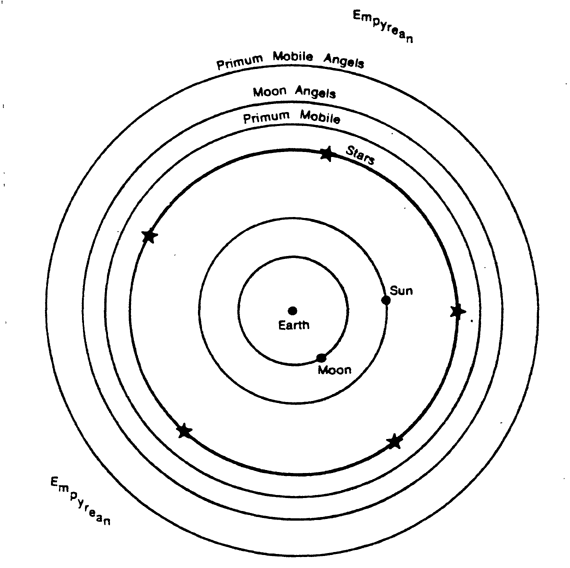
Aristotle had believed that the world was a series of nine spheres centered around the Earth. The last of these crystalline spheres was called the Primum Mobile and lay beyond the sphere upon which were fastened all of the stars (other than the sun, which was attached to the fourth sphere). In the Paradisio, Dante is led out through space by Beatrice. He passes through each of the nine spheres of the world: Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn, Fixed Stars, Primum Mobile. Beyond these nine spheres lie nine spheres of angels, corresponding to the nine spheres of the world. Beyond the nine spheres of angels lies a point called the Empyrean, which is the abode of God.

The puzzling thing about Dante's cosmos as it is drawn in Figure 14 is that here the Empyrean appears not to be a point, but rather to be all of space (except for the interior of the last sphere of angels). But this can be remedied if we take space to be hyperspherical! In Figure 15 I have drawn the model we obtain if we take the diagram on the last page and curve it up into a sphere with a point-sized Empyrean. In the same way, the three-dimensional model depicted by the first picture can be turned into the finite unbounded space of the second picture if we bend our three-dimensional space in such a way that all of the space outside our last angelic sphere is compressed to a point.²¹ Figure 16 is Doré's engraving of the Empyrean surrounded by its spheres of angels.

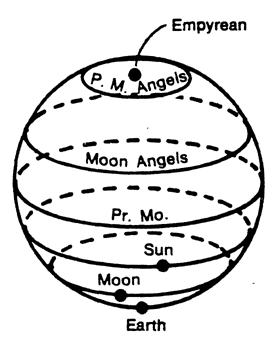
This whole notion of hyperspherical space was not consciously developed until the mid-nineteenth century. In the Middle Ages there was a general and uncritical acceptance of Aristotle's view of the universe -- without Dante's angelic spheres.

Lucretius, of course, had insisted that space is infinite, and there were many other thinkers, such as Nicolas of Cusa and Giordano Bruno, who believed in the infinitude of space. Some kept to the Aristotelian world system, but suggested that there were many such setups drifting around; others opted for a looser setup under which stars and planets are more or less randomly mixed together in infinite space.

Bruno strongly advocated such viewpoints in his writings, especially his dialogue of 1584, "On the Infinite Universe and Worlds."²² Bruno travelled freely around Europe during his lifetime, teaching his doctrine of the infinite universe at many centers of learning. In 1591, a wealthy Venetian persuaded Bruno to come from Frankfurt to teach him "the art of memory and invention." Shortly after Bruno arrived, the trap was sprung. His host had been working closely with the ecclesiastical authorities, who considered Bruno a leading heretic or heresiarch. Bruno was turned over to the Inquisition. For nine years Bruno was interrogated, tortured, and tried, but he would not give up his beliefs; early in 1600 he was burned at the stake in the Roman Piazza Campo di Fiori. Bruno's example caused Galileo to express himself a good deal more cautiously on scientific questions in which the Church had an interest.

Whether or not our space is actually infinite is a question that could conceivably be resolved in the next few decades. Assuming that Einstein's theory of gravitation is correct, there are basically two types of universe: i) a hyperspherical (closed and unbounded) space that expands and then contracts back to a point; ii) an infinite space that expands forever. It is my guess that case i) will come to be most widely accepted, if only because the notion of an actually infinite space extending out in every direction is so unsettling. The fate of the universe in case i) is certainly more interesting, since such a universe collapses back to an infinitely dense space-time singularity that may serve as the seed for a whole new universe. In case ii), on the other hand, we simply have cooling and dying suns drifting further and further apart in an utterly empty black immensity . . . and in the end there are only ashes and cinders in an absolute and eternal night.

Even though I am basically pro-infinity, my emotions lie with the hyperspherical space. But is there any way of finding a spatial infinity here? Well, what about that four-dimensional space in which our hyperspherical universe is floating? Many would dismiss this space as a mere mathematical fiction . . . as a colorful way of expressing the finite, but unbounded, nature of our universe. This widely held position is really a more sophisticated version of Aristotle's claim that what is limited need not be limited with reference to something outside itself.

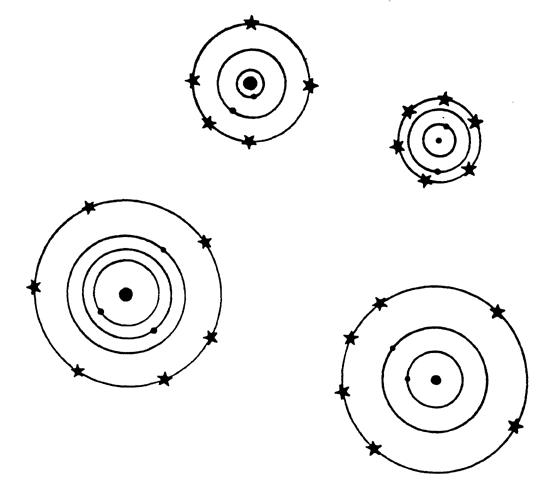
But what if one chooses to believe that the four-dimensional space in which our universe curves is real? We might imagine a higher 4-D (four-dimensional) world called, let us say, a duoverse. The duoverse would be 4-D space in which a number of hyperspheres were floating. The hypersurface of each of the hyperspheres would be a finite, unbounded 3-D universe.

Thus, a duoverse would contain a number of 3-D universes, but no inhabitant of any one of these universes could reach any one of the others, unless he could somehow travel through 4-D space. By lowering all the dimensions by one, one can see that this situation is analogous to a universe that is a 3-D space in which a number of spheres are floating. The surface of each sphere or planet is a finite, unbounded 2-D space; and no one can get from one planet surface to another planet surface without travelling through 3-D space.

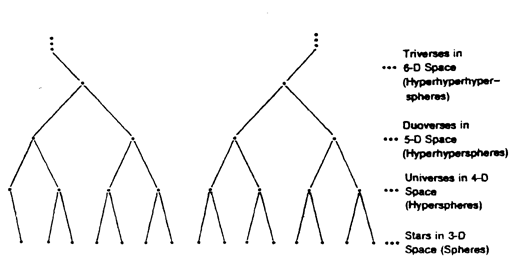
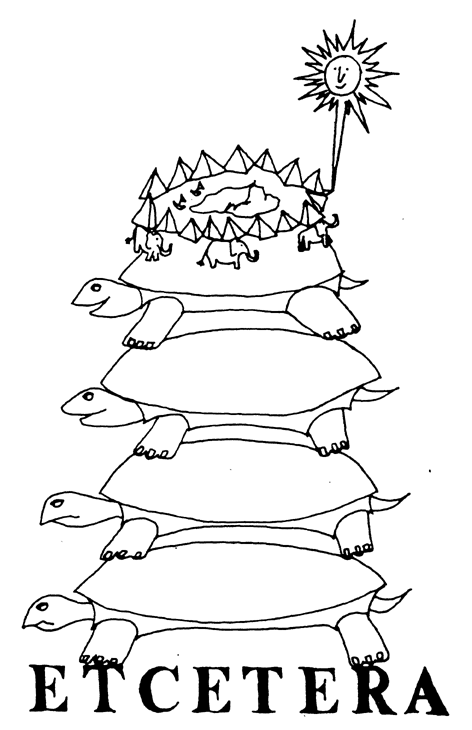
Following the Hermetic principle, "As above, so below," one is tempted to believe that the duoverse we are in is actually a finite and unbounded 4-D space (the 4-D surface of a 5-D sphere in 5-D space), and that there are a number of such duoverses drifting about in a 5-D triverse. This could be continued indefinitely. One is reminded of those Eastern descriptions of the world as a disk resting on the backs of elephants, who stand upon a turtle, who stands upon a turtle, who stands upon a turtle, who stands upon a turtle, etc.

Note that in that particular sort of cosmos there is only one universe, one duoverse, one triverse, and so on. But in the kind of infinitely regressing cosmos that I have drawn in Figure 18, we have infinitely many objects at each level. Note also that to get from star A to star B one would have to move through 5-D space to get to a different duoverse. It is a curious feature of such a cosmos that, although there are an infinite number of stars, no one n-dimensional space has more than a finite number of them.

The question we are concerned with here is whether or not space is infinitely large. There seem to be three options: i) There is some level n for which n-dimensional space is real and infinitely extended. The situation where our three-dimensional space is infinitely large falls under this case. ii) There is some n such that there is only one n-dimensional space. This space is to be finite and unbounded, and there is to be no reality to n + 1 dimensional space. The situation where our three-dimensional space is finite and unbounded, and the reality of four-dimensional space denied, falls under this case. iii) There are real spaces of every dimension, and each of these spaces is finite and unbounded. In this case we either have an infinite number of universes, duoverses, etc., or we reach a level after which there is only one n-verse for each n.

So is space infinite? It seems that we can insist that at some dimensional level it is infinite; adopt the Aristotelian stance that space is finite at some level beyond which nothing lies; or accept the view that there is an infinite sequence of dimensional levels. In this last case we already have a qualitative infinity in the dimensionality of space, and we may or may not have a quantitative infinity in terms, say, of the total volume of all the 3-D spaces involved.

Infinities in the Small

In this subsection I will discuss the existence of the infinity in the small, as opposed to the infinity in the large, which has just been discussed. Since a point has no length, no finite number of points could ever constitute a line segment, which does have length. So it seems evident that every line segment, or, for that matter, every continuous plane segment or region of space, must consist of an infinite number of points. By the same token, any interval of time should consist of an infinite number of instants; and any continuous region of space-time would consist of an infinite number of events (event being the technical term for a space-time location, i.e., point at an instant).

It is undeniable that a continuous region of mathematical space has an infinite number of mathematical points. Right now, however, we are concerned with physical space. We should not be too hasty in assuming that every property of the abstract mathematical space we use to organize our experiences is an actual property of the concrete physical space we live in. But what is "the space we live in"? If it is not the space of mathematical physics, is it the space of material objects? Is it the space of our perceptions? In terms of material objects or of perceptions, points do not really exist; for any material or perceptual phenomenon is spread over a certain finite region of space-time. So when we look for the infinity in the small in matter, we do not ask whether matter consists of an infinity of (unobservable) mass-points, but, rather, whether matter is infinitely divisible.

A commitment to avoiding the formless made it natural for Greek atomists such as Democritus to adopt a theory of matter under which the seemingly irregular bodies of the world are in fact collections of indivisible, perfectly formed atoms. (The four kinds of atoms were shaped, according to Plato, like four of the regular polyhedra. There is one other polyhedron, the twelve-sided dodecahedron, and this was thought somehow to represent the Universe with its twelve signs of the zodiac.) For the atomists, it was as if the world were an immense Lego set, with four kinds of blocks. The diverse substances of the world -- oil, wood, stone, metal, flesh, wine, and so on -- were regarded as being mixtures of the four elemental substances: Earth, Air, Fire, and Water. Thus, gold was regarded by Plato as being a very dense sort of Water, and copper was viewed as gold with a small amount of Earth mixed in.

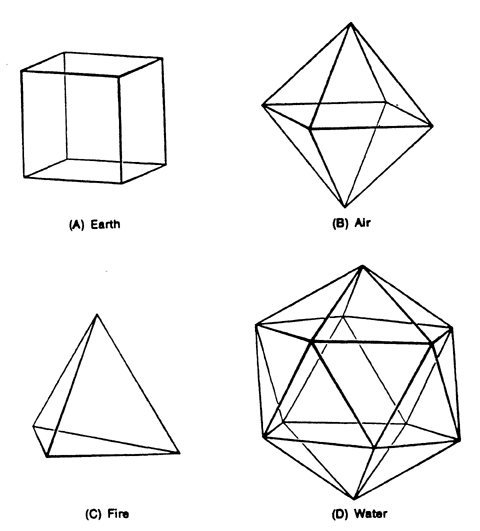
Figure 20. (A-D). From D. Hilbert and H. Cohn-Vossen, Geometry and the Imagination.

The alchemists and early chemists adopted a similar system, only the number of elemental substances became vastly enlarged to include all homogeneous substances, such as the various ores, salts, and essences. The fundamental unit here was the molecule.

A new stage in man's conception of matter came when it was discovered that if an electric current is passed through water, it can be decomposed into hydrogen and oxygen. Eventually, the vast diversity of existing molecules was brought under control by regarding molecules as collections of atoms. Soon some ninety different types of atoms or chemical elements were known. A new simplification occurred when it was discovered, by bombarding a sheet of foil with alpha rays, that an atom consists of a positive nucleus surrounded by electrons. Shortly after this the neutron was discovered, and the physical properties of the various atoms were accounted for by regarding them as collections of protons, neutrons, and electrons.

Over the last half century it has been learned, by using particle accelerators, that there are actually many types of "elementary particles" other than the neutron, electron, and proton. The situation in high-energy physics today is as follows. A few particles -- electrons, neutrinos, and muons -- seem to be absolutely indivisible. These particles are called leptons. All others -- protons, neutrons, mesons, lambdas, etc. -- can be broken up into smaller units, which then reassemble to form more particles.

The historical pattern in the investigation of matter has been the explanation of diverse substances as combinations of a few simpler substances. Diversity of form replaces diversity of substance. So it is no surprise that it has been proposed that the great variety of divisible particles that exist can be accounted for by assuming that these particles are all built up out of quarks.

A second element in the historical pattern is that as more powerful tools of investigation are used, it becomes evident that there are more types of new building blocks than had been suspected initially. This is the phase that high-energy physics is currently moving into. First there were three kinds of quark: up, down, and strange. Now, the charmed quark has been admitted, and there are two new possible quarks: the top quark and the bottom quark. It seems likely that the many diverse types of quark will eventually be accounted for by assuming that each quark is a combination of a few, let us say, darks . . . and that there are only a very small number of possible kinds of dark. The cycle will then repeat, with more and more different sorts of dark being indirectly observed, the new diversity being accounted for by viewing each dark as a collection of a few smaller particles of which there are a limited variety, this limited variety beginning to proliferate, and so on.

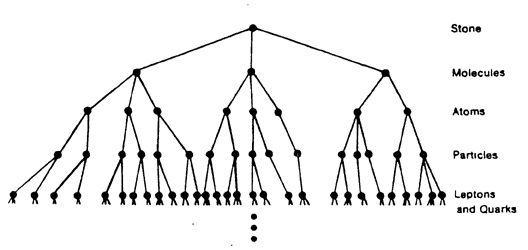
If this sort of development can indeed continue indefinitely, then we are left with the fact that a stone is a collection of collections of collections of. . . . The stone thus consists of an infinite number of particles, no one of which is indivisible. There is, finally, no matter -- only form. For a stone is mostly empty space with a few molecules in it, a molecule is a cloud of atoms, an atom is a few electrons circling a tiny nucleus. . . . What if any seemingly solid bit of matter proves on closer inspection to be a cloud of smaller bits of matter, which are in turn clouds, and so on? Note that the branching matter tree that I began to draw for the stone has only a finite number of forks or nodes at each level, but that since there are infinitely many levels, there are in all an infinite number of nodes or component particles.

There are various objections to this sort of physical infinity. One is the Aristotelian argument that unless one is actually smashing the stone down to the quark level, the quarks are only potentially (as opposed to actually) there. The point would be that the stone may be indefinitely divisible, but that since no one will ever carry out infinitely many divisions, there are not really infinite numbers of particles in the stone right now.

There is a more practical objection as well. This is that no quark has ever been observed in isolation; the existence of quarks is deduced only indirectly as a way of explaining the symmetries of structure that occur in tables of the elementary particles. This argument is not very strong, however. For one thing, a great number of the things we believe in can be observed only indirectly; and, more practically, if we can continue to increase the energy of our measuring tools, there is no reason to think that quarks cannot be more convincingly detected.

A more fundamental objection to the whole idea of particles, subparticles, etc., is that the underlying reality of the world may be field-like, rather than particle-like. By splitting particles indefinitely we arrived at the conclusion that there is only form, and no content; many physicists prefer to start with this viewpoint. For these physicists, the various features of the world are to be explained in terms of the geometry of space-time. To get a feeling for this viewpoint, one should look carefully at the surface of a river or small brook. There are circular ripples, flow bulges, whirlpools and eddies, bubbles that form, drops that fly up and fall back, waves that crest into foam. The geometrodynamic worldview regards space-time as a substance like the surface of a brook; the various fields and particles that seem to exist are explained as features of the flow.

Does the space-time of geometrodynamics allow an infinity in the small? There is really no answer to this question at present. According to one viewpoint there should be a sort of graininess to space-time, and the grain size would represent a sort of indivisible atom; a different viewpoint suggests that space-time should be as infinitely continuous as mathematical space.

What if there really is nothing smaller than electrons and quarks? Is there then any hope of an infinity in the small? One can argue that a given electron can have infinitely many locations along a given meter stick, so that our space really does have infinitely many points. It is sometimes asserted that the uncertainty principle of quantum mechanics nullifies this argument, but this is not the case.

Quantum mechanics puts no upper limit on the precision with which one can, in principle, determine the position of an electron. It is just that the more precisely the electron's position is known, the less precisely are its speed and direction of motion known. Infinite precision is basically a nonphysical notion, but any desired finite degree of precision is, in principle, obtainable. The precision with which something can be measured is thus a good example of something that is potentially infinite, but never actually infinite.

But this still gives us an actual infinity in the world. For if our electron is located somewhere between zero and one, then each member of the following infinite collection is a possible outcome of a possible measurement:

 .2 ± .1, .23 ± .01, .235 ± .001,
.2356 ± .0001, . . . , .235608947 ± .000000001, . . . 

Although infinite precision is impossible, an electron can be found to occupy any of the infinitely many points between zero and one whose distance from zero is a terminating decimal.

There are, however, some modern physical speculations that regard "space" and "time" as being abstractions which apply to our size level, but which become utterly meaningless out past the thirtieth decimal place. What would be there instead? Our old friend the apeiron. But even if we cannot really speak of infinitely many space locations, we might hope to find infinitely many sorts of particle.

It is sometimes thought that quantum mechanics proves that there is a smallest size of particle that could exist. This is not true. Quantum mechanics insists only that in order to "see" very small particles, we must use very energetic processes to look for them.

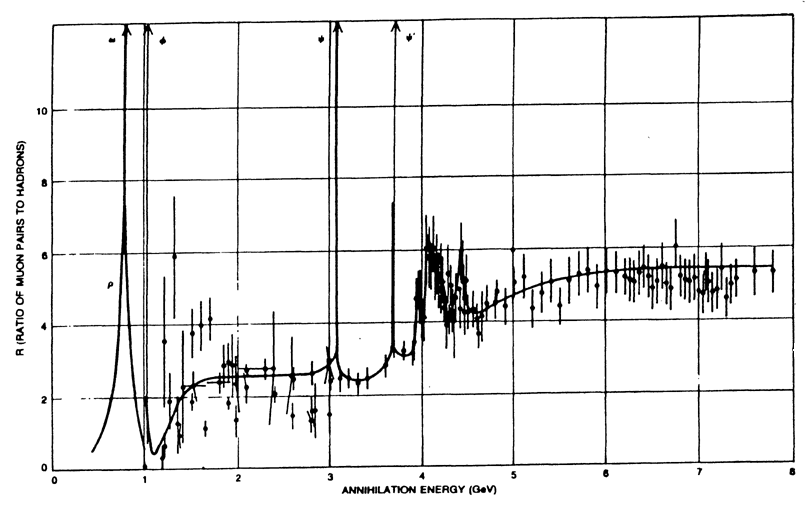
It is illuminating, after all this, to learn how the high-energy physicists actually go about finding new particles. The process is a little like finding stations on the radio by inching the dial back and forth until you hear music instead of static. One uses a particle accelerator in which collisions (between electrons and positrons) are continually taking place. The energy of the collision processes is varied by turning the voltage on the accelerator up and down. There is number R that measures the "particleness" of the reaction taking place. R can be thought of as being a little like the information parameter that enables you to tell whether you have found a station, even though the sound of music is no louder than the sound of the static. When an energy is found at which the graph of R versus energy has a sudden peak, then it is assumed that the energy in question is characteristic of the rest-mass of a new particle. This process is called "bump-hunting." It is interesting to note that the sharper and narrower the peak, the more long-lived, and, thus, more "real" the particle is.

The question of whether or not matter is infinitely divisible may never be decided. For whenever an allegedly minimal particle is exhibited, there will be those who claim that if a high enough energy were available, the particle could be decomposed; and whenever someone wishes to claim that matter is infinitely divisible, there will be some smallest known particle which cannot be split. One is almost tempted to doubt if the question of the infinite divisibility of matter has any real meaning at all, particularly in view of the fact that such concepts as "matter" and "space" have no real meaning in the micro-world of quantum mechanics.

To return to something a little more concrete, let us consider the divisibility of our perceptual field. There is a limit to the subdivisions that this field can undergo. If two clicks happen close enough together in time, they cannot be distinguished; if a spot of ink is small enough, we can no longer see it. Hume makes much of this fact in his Treatise of Human Nature of 1739:

Put a spot of ink upon paper, fix your eye upon that spot, and retire to such a distance, that at last you lose sight of it; 'tis plain, that the moment before it vanish'd the image or impression was perfectly indivisible.²³

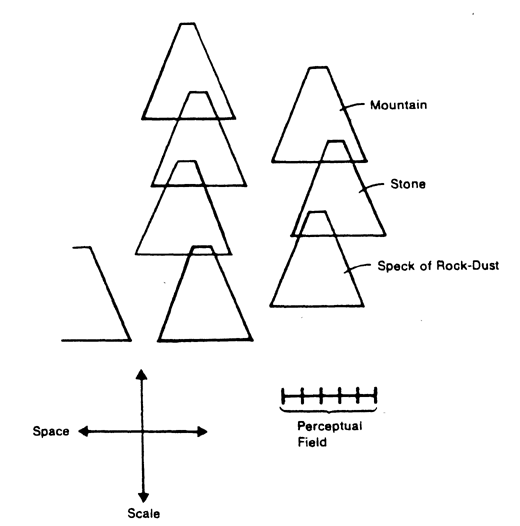
The best way to understand Hume's view of the world is to regard our space-time as being supplemented by an additional dimension of scale. To represent what I have in mind, let us forget about time and drop all the space dimensions but one. In Figure 24 I have drawn the space-scale continuum for a one-dimensional world. An individual's perceptual field has a certain fixed size, as drawn; the field is made up of a certain finite number of slots or tiles -- minimal perceptual units. In this model, the one-dimensional creature has two dimensions in which he can move his perceptual field. He can move to the left and right in space, and he can enlarge and contract his perceptual field. Rather than thinking of the field as enlarging and contracting, we think of the field moving up and down on the scale axis.

If the labelled objects (mountain, stone, speck of rock dust) occupy the appropriate regions of the space-scale continuum, then we can think of the ordinary perceptual level as being when the field is placed somewhere in the middle of the picture. At this perceptual level stones are visible, but one has neither enlarged one's field of vision enough to see the mountain as a single object, nor contracted one's attention enough to see the specks of dust on the rock. Notice that changing the size of one's perceptual field amounts just to moving this field about in the space-scale continuum.

Hume takes perceptions as primary. Although he is often thought of as an empiricist, his is actually an extremely idealistic viewpoint. The perceptions are "out there"; one's consciousness seems to move among them like a butterfly flitting from flower to flower.

One's perceptual field has minimal elements, yet these minimal elements can be resolved into smaller elements by altering one's field (by paying closer attention, using a telescope, or moving closer to the object in question). The only way to reconcile these two apparently contradictory aspects of our perceptual world is to view the world as a five-dimensional, space-time-scale continuum.

The question of the existence of an infinity in the small now becomes the question of whether or not the space-scale continuum drawn in Figure 24 extends downward indefinitely; similarly, the question of the existence of infinity in the large is the question of whether or not the continuum extends upward indefinitely.

I have long been interested in a curious trick that eliminates the infinity in the large and the infinity in the small without introducing any absolute perceptual minimum or maximum. This is simply the trick of bending the space-scale diagram into a tube, by turning the scale axis into a circle. Here the universe could consist of many galaxies, which consist of many star systems, which consist of many planets, which consist of many rocks, which consist of many molecules, which consist of many atoms, which consist of many elementary particles, which consist of many quarks and leptons, which consist of many darks, which could consist of many universes.²⁴

A problem with the circular scale model is that if our universe is broken down far enough, one gets many universes, each of which will break down into many more universes. Are all of these universes the same? Perhaps, but then it would be hard to see how there could really be more than one object in the world. Another difficulty is that if there are many universes, each of which breaks up into many more universes, how can each of the component universes be one of the starting universes?

There is no problem if we have infinitely many universes. To illustrate this, I have drawn a picture of the simplest case: the case in which each universe is made up of two universes. We can see that 1 splits into 1 and 2, 2 splits into 3 and 4, 3 splits into 5 and 6, and in general n splits into 2n - 1 and 2n. We can continue splitting any given universe indefinitely, thus obtaining an infinite number of components in any bit of matter.

What is gained here is freedom from the belief that any size scale is intrinsically more basic or important or complex than any other size scale. Why waste time on the six o'clock news when you are no more nor less important than a galaxy or an atom? The point of this question is that one is often pressured to feel that the concerns of society or the world are more significant than one's own immediate personal concerns. But this is based on the assumption that some sizes are in an absolute sense bigger than others, and it is this assumption that circular scale undermines.

Conclusion

In conclusion, note that it is entirely possible that our universe is in every sense finite. A toroidal space-time of the sort mentioned in the section on temporal infinities eliminates all infinities in the large; and if circular scale is introduced as in the section on infinities in the small, then there are no discrete infinities in the small. These finitizations can be accomplished smoothly: there need be no end of time, edge of space, or smallest particle.

But it is hard to believe that there would be only one of these totally finite universes. First, it is difficult to see how to apply circular scale unproblematically unless there are infinitely many universes; second, the principle of sufficient reason is violated if only this particular finite universe exists; and third, there is the feeling that the "space" in which our space-time is curved should be real.

In the section on spatial infinities it was pointed out that if, on the one hand, one repeatedly finitizes by replacing lines with circles, and if, on the other hand, one never accepts some particular finite n-verse as the end of the line -- if, in other words, one thinks along the lines sketched in the last two paragraphs --then one is forced to conclude that space is infinite dimensional and that there are infinitely many objects in this cosmic space.

INFINITIES IN THE MINDSCAPE

In the last section I discussed some of the ways in which an actual infinity could physically arise. But there are things that are not physical. There are minds, thoughts, ideas, and forms. In this section we will see if any of these familiar nonphysical entities are actually infinite.

In order to appreciate the section at hand, it is necessary to keep an open mind on the question of whether or not mind equals brain, for if one assumes a priori that a thought is nothing more than a certain biochemical configuration in a certain finite region of matter, then (unless one has infinite divisibility of matter) it seems to follow automatically that infinite thoughts are impossible.

To cast a few preliminary doubts on the hypothesis that brain equals mind, let me quickly raise a few questions. Is what you thought yesterday still part of your mind? If you own and use an encyclopedia, are the facts in that encyclopedia part of your mind? Does a dream which you never remember really exist? How can you grasp a book as a whole, even though you only read it a word at a time? Would the truths of mathematics still exist if the universe disappeared? Did the Pythagorean theorem exist before Pythagoras? If three people see the same animal, we say the animal is real; what if three people see the same idea?

I think of consciousness as a point, an "eye," that moves about in a sort of mental space. All thoughts are already there in this multi-dimensional space, which we might as well call the Mindscape. Our bodies move about in the physical space called the Universe; our consciousnesses move about in the mental space called the Mindscape.

Just as we all share the same Universe, we all share the same Mindscape. For just as you can physically occupy the same position in the Universe that anyone else does, you can, in principle, mentally occupy the same state of mind or position in the Mindscape that anyone else does. It is, of course, difficult to show someone exactly how to see things your way, but all of mankind's cultural heritage attests that this is not impossible.

Just as a rock is already in the Universe, whether or not someone is handling it, an idea is already in the Mindscape, whether or not someone is thinking it. A person who does mathematical research, writes stories, or meditates is an explorer of the Mindscape in much the same way that Armstrong, Livingstone, or Cousteau are explorers of the physical features of our Universe. The rocks on the Moon were there before the lunar module landed; and all the possible thoughts are already out there in the Mindscape.

The mind of an individual would seem to be analogous to the room or to the neighborhood in which that person lives. One is never in touch with the whole Universe through one's physical perceptions, and it is doubtful whether one's mind is ever able to fill the entire Mindscape.

One last analogy. Note that there is always a certain region of physical space that only I can ordinarily know of -- barring surgery, no one but me is in a position to assess the physical conditions obtaining within my stomach. In the same way, there is a certain part of the Mindscape that only I can ordinarily know of -- unless I am to be greatly favored by the Muse, the feelings that pass over me when I think of my childhood will always remain private and inexpressible. Nevertheless, these almost ineffable feelings are part of the common Mindscape -- they are simply difficult for anyone else to get to.

The point of all this is that just as the finiteness of our physical bodies does not imply that every physical object is finite, the finiteness of the number of cells in our brains does not mean that every mental object is finite.

Well . . . are there any infinite minds, thoughts, ideas, or forms or what have you in the Mindscape?

The most familiar candidate is the set N of all natural numbers. If I try to exhibit N, all I can really do is show you something like this: N = {1, 2, 3, . . .]. What the ". . ." stands for is something that is evident, yet basically inexpressible. The idea, of course, is that all of the natural numbers are to be collected together into a whole. Each of them would seem to exist individually in the Mindscape, and one would suppose that the set consisting of exactly the natural numbers would be in the Mindscape as well -- one almost feels as if one can see it.

We might try to avoid the use of the ". . ." by saying something like this: "N is the set that has the following property: one is in N, and for any number x that is in N, x plus one is in N as well." The trouble with this definition is that it does not uniquely single out one particular set. If, for instance, there were some infinitely large number I, and if N* were the set consisting of all the numbers in N and all the numbers of the form I + n for some n in N, then N* would satisfy the property that for every x in N*, x plus one is in N* as well . . . but N* would be different from N.

We might try to get around this difficulty by saying that N is the smallest set in the Mindscape that has one in it, and that has x plus one whenever it has x. But, for reasons that I will begin to explain in the next section, the word "Mindscape" cannot be meaningfully used in a definition. The concept of "Mindscape" is too vast to be represented by any word or symbol.

If we try to avoid this difficulty by substituting some sort of finite description of the mental universe for the word "Mindscape," then we get the same problem as before. By the classic work of the logician Thoralf Skolem, we know that for any finite description of N one might come up with, there will be a different set N* that also satisfies the description. So it is quite literally true that what is really meant by the ". . ." is inexpressible.

Some thinkers have taken this to mean that there is, after all, no unique N in the Mindscape. This could be true. But one need not take this to mean that there are no infinite sets in the Mindscape: if there are many, many versions of the set of natural numbers, then there are many, many infinite sets. However, it is normally more desirable to assume that there is a simple unique N in the Mindscape, just as it is simpler to assume that there is only one universe instead of a whole slew of "parallel worlds."

I might note here that if time is indeed infinite, then just as we can indicate Earth by saying, "this planet," we could indicate our N by saying, "the number of seconds left in this time." This is, in fact, what people do when they attempt to define N by saying, "N is what you get if you start with one and keep adding ones forever."

If infinite forms are actually out there in the Mindscape, then maybe we can, by some strange trick of mental perspective, see some of these forms. The philosopher Josiah Royce maintained that a person's mental image of his own mind must be infinite.²⁵ His reason is that one's image of one's own mind is itself an item present in the mind. So the image includes an image that includes an image, and so on. This infinite regress can be nicely visualized by imagining a United States in which a vast and fanatically accurate scale model of the country occupies most of the Midwest. The scale model, being absolutely accurate, includes a copy of the scale model, etc. This regress is occasionally used to make a striking label for a commercial product. The old can of Pet Milk, for instance, bore a picture of a can of Pet Milk, which bore a picture of a can of Pet Milk, etc.

In a physical situation we would probably never actually be able to finish making such a label in all its infinite detail. But this is not to say that no such label or country-plus-scale-model could exist. There would be no problem, if matter were infinitely divisible. (If scale is indeed circular, then everything is, in a sense, already an object of this nature!)

There is certainly no reason why a nonphysical mind should not be infinite; and Royce's point is that if you believe that one of the things present in your mind is a perfect image of this mind and its contents, then your mind is infinite. One might try to avoid this conclusion by adopting a circular scale attitude and insisting that there is no difference between the mind and the mind's image of itself, so that the allegedly infinite set of thoughts {image of the mind, image of the image, image of the image of the image, . . .} is really the same as the set {mind, mind, mind, . . .}, which is just a set with one member: {mind}.

I would like to discuss this a bit more, but first let me formally introduce some of the apparatus of set theory. In Cantor's words, "A set is a Many that allows itself to be thought of as a One."²⁶ A set is usually given as a pair of curly brackets enclosing some description of the contents of the set. It is easiest to think of the curly brackets as a thought balloon. Thus the set {1, 2} is the unity obtained by taking the multiplicity consisting of the numbers 1 and 2 and treating this multiplicity as a unity. That is, we can think of the set {1, 2} as being represented by a thought balloon that has 1 in it and 2 in it.

Of particular interest in set theory is the empty set, �. � is the One obtained by taking together . . . nothing. If we write out � in the ordinary way we get { }, which I have drawn as an empty thought balloon.

More and more complicated sets can be built up using only the brackets in various arrangements. Thus we have the set {{ }} depicted in Figure 28B, and we could equally well form {{ }, {{ }}, {{ }, {{ }}}} which is how the number 3 is usually represented in terms of pure sets. (See Figure 29.)

Now let's get back to the question of whether or not a mind that has a perfect self-image is infinite. Really to get down to the bare bones, say that we have a mind or label or set M such that the only member of M is M. That is, M = {M}. Now, if we change this equation by replacing the M on the right by {M} then we get M = {{M}}. If we could continue replacing M by {M} forever, we would wind up with M = {{{{{. . . . . .}}}}}. This could actually be a definition of an M whose only member is itself, for note that placing another pair of brackets around {{{{{. . . . . .}}}}} changes nothing. In plain English, M is the set whose only member is the set whose only member is . . .

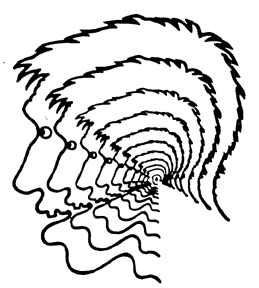
Figure 30. Based on a drawing from Robert Crumb, Your Hytone Comix (San Francisco: The Print Mint, 1976).

But if the only member of M is indeed M itself (rather than a copy of M), then M really only has one element. It is just that if we try to describe this element by using brackets we get an infinite description. We call thoughts like M self-representative. Whether or not such an M is to be regarded as infinite depends on whether you experience the M subjectively (in the way you experience your own mind), or objectively (as a feature of the Mindscape that is to be precisely described in the language of set theory).

Set theory is, indeed, the science of the Mindscape. A set is the form of a possible thought. Set theory enables us to put various facts about the Mindscape into one framework in the same way that the atomic theory of matter provides a framework in which the diverse physical and chemical qualities of matter can be simultaneously accommodated.

Before the atomic theory of matter, such phenomena as melting and burning, rusting and freezing were regarded as qualitatively different. Once a good atomic theory was developed, however, all of these phenomena could be thought of in more or less the same way. The notion of set was consciously introduced only at the turn of the century. Before long, it became evident that all of the objects that mathematicians discuss -- functions, graphs, integrals, groups, spaces, relations, sequences --all can be represented as sets. One can go so far as to say that mathematics is the study of certain features of the universe of set theory.

The universe of set theory is closely bound up with the Mindscape -- one can, perhaps, think of the former as a sort of blueprint of the latter. A set is obtained when we take a thought and abstract from it all the emotive content, keeping only the abstract relational structure. A set is the form of a possible thought. So the question of whether or not there are any infinite entities in the Mindscape is really equivalent to the question of whether or not there are any infinite sets.

According to set theorists, there certainly are infinite sets. Indeed, there is to be an endless hierarchy of infinities: the set of natural numbers, the set of all sets of natural numbers, the set of all sets of sets of natural numbers, etc. Each member of this sequence can be shown to be of an infinity greater than that of the earlier members. In modern set theory there is a whole field of study called large cardinals, whose specialists study a dizzying array of higher and higher infinities.

But many mathematicians and philosophers do not go along with the set theorists. The traditional finitist viewpoint is still with us. According to the finitists, there is nothing that is infinite, in heaven or on earth.

Those who assert that infinite sets of every size have a secure existence in the Mindscape are usually called Platonists. This name is a bit inapt, since Plato did not believe in infinity; but he did believe in the existence of ideas independent of thinkers, and it is for this aspect of his thought that the Platonists are named.

It is not likely that the finitist vs. Platonist debate will ever be concluded. On the one hand, it is probably impossible to meet the demands of a finitist who says that he will believe in infinity only if he is shown an infinite set right now; on the other hand, the notion of infinite sets appears to be logically consistent, so the finitist can never prove that infinite sets do not exist.

I incline towards Platonism; but if you are stubborn enough, how can I possibly convince you that infinite things are real? All I can do, after all, is to make a finite number of marks on a finite number of sheets of paper. If you are truly committed to disbelief in the infinite, then you will not be satisfied by anything less than my simultaneously exhibiting each member of some infinite set . . . and whenever I claim that I have done so, you will triumphantly point at the finiteness of the number of marks on paper which I have really shown you.

In pre-Cantorian times finitists sometimes thought that they had proved the impossibility of actually infinite sets. These proofs, however, were always fallacious. Such proofs usually deal with some particular property P of numbers that each natural number happens to enjoy. P might be the property of being odd or even, having an immediate predecessor, being the sum of finitely many units, or being greater than any predecessor. The false proof that no infinite numbers exist then takes the form: "Every number has property P. If x is an infinite number, then x cannot have property P. Therefore no infinite numbers can exist." The fallacy in such a circular proof is that when it is asserted that "every number has property P," it is being quietly assumed that anything that fails to have property P does not exist.

But, of course, one cannot assume that the infinite sets must have certain properties before one has ever looked at them! Galileo's paradox, for example, showed that an infinite set can be put into a one-to-one correspondence with a proper subset of itself. Had we assumed in advance that no set could be put into a one-to-one correspondence with a proper subset of itself, then we would have had a proof that no infinite set can exist. But such an assumption is totally unwarranted; indeed, to make such an assumption is essentially to assume in advance that every set is finite . . . which does not make for a very productive debate.

But are we quite sure that the finitists will never come up with some valid proof that the notion of infinite sets is incoherent and fundamentally meaningless? A Platonist would answer that yes, he is sure that there is no inconsistency in the theory of infinite sets. He is sure of this because the theory in question is a description of certain features of the Mindscape that "anyone can see."

But the finitist can still hope. There is a curious proof, discovered by Kurt Gödel in 1930, that the consistency of set theory cannot be finitely proved. The time will never come when the finitist is absolutely forced to admit that it is safe to talk about infinite sets.

In mathematics no other subject has led to more polemics than the issue of the existence or nonexistence of mathematical infinities. We will return to some of these polemics in the last chapter. For now, let us reprint Cantor's opening salvo in the modern phase of this age-old debate:

The fear of infinity is a form of myopia that destroys the possibility of seeing the actual infinite, even though it in its highest form has created and sustains us, and in its secondary transfinite forms occurs all around us and even inhabits our minds.²⁷

Strong words! But what does Cantor mean when he says that the highest form of infinity created us? Read on!

THE ABSOLUTE INFINITE

There is a certain type of non-physical entity that was not discussed in the last section. God, the Cosmos, the Mindscape, and the class V of all sets -- all of these are versions of what philosophers call the Absolute. The word "Absolute" is used here in the sense of "non-relative, non-subjective." An Absolute exists by itself, and in the highest possible degree of completeness.

As I mentioned earlier, Plotinus held that the One could not be limited in any sense. As Aquinas, the quintessential theologian, says: "The notion of form is most fully realized in existence itself. And in God existence is not acquired by anything, but God is existence itself subsistent. It is clear, then, that God himself is both limitless and perfect."²⁸

The limitlessness of God is expressed in a form closer to the mathematical infinite by St. Gregory: "No matter how far our mind may have progressed in the contemplation of God, it does not attain to what He is, but to what is beneath Him."²⁹ We have here the rudiments of the infinite dialectic process that takes place if we systematically try to build up an image of the whole Mindscape.

Suppose that I want to add thought after thought to my mind until my mind fills the whole Mindscape. Whenever I make an attempt at this, I am collecting together a group of thoughts into a single thought T. Now, when I become conscious of my state of mind T, I realize that this is a new thought that I had not yet accounted for . . . so I improve my image of the Mindscape by passing to the thought that includes all the elements of T plus T itself, viewed objectively.

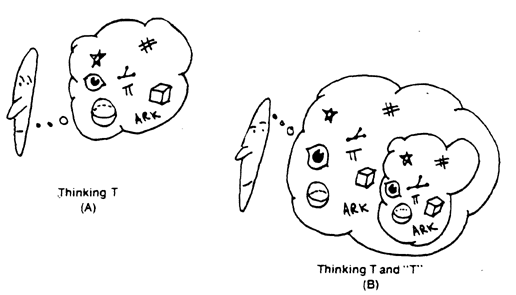
This is a dialectic process in the sense that the thetic component is one's instantaneous unconscious image of the Absolute, the antithetic component is the conscious formalization of this image, and the synthetic component is the formation of a new unconscious image of the Absolute that incorporates one's earlier images and the awareness that they are inadequate.³⁰

This process is most clearly understood if we start with nothing at all, as in the cartoon strip of Wheelie Willie in Figure 32. (Wheelie Willie is a character whose adventures I occasionally used to draw for the Rutgers Daily Targum when I was in graduate school there.) Notice that in each of the shifts, what takes place is that Wheelie Willie forms a thought that has as its members the members of the last thought plus the last thought itself. Looked at another way, the thought at each stage has all of the previous stages as components.

If we call the nth thought T_n we can define T_n in two ways. On the one hand, we can use an inductive definition: T_o = � and T_{n + 1} = T_n 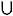{T_n}, where for any sets A and B, A 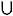B means the set of all the sets that are members of A or of B. On the other hand, we can use a different sort of inductive definition: T_n = {T_m:m < n}, which means "T_n is the set of all T_m such that m is less than n."

Some readers may have asked themselves if the thought T plus "T" really has to be different from the thought T. And the answer is, not always. In the last section we were looking at a mind, M, which has M as one of its components. Such an M is already fully self-aware, and M plus "M" is no different from M. In terms of sets, M 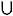{M} = M.

It would seem, in particular, that God should be able to form a precise mental image of Himself. Insofar as the Mindscape is God's mind, what I am saying is that one of the objects in the Mindscape should be the Mindscape itself. That is, the Mindscape is an M that has M as one of its members. Now, any object in the Mindscape is, in principle, something that one can perceive through one's consciousness. So it would seem to be possible for our minds actually to attain a vision of God or of the whole Mindscape.

Now this seems to contradict St. Gregory's dictum and the general feeling that the Absolute is unknowable. But there are two kinds of knowing: the rational and the mystical.

If I know something rationally, then I have some thought that is built up from simpler thoughts, which are in turn built up from still simpler thoughts. This regress is not infinite, but goes only through some finite number of stages before certain simple and unanalyzable perceptions and ideas are reached. My idea of "house" consists of a collection of ideas, each one of which represents a certain type of house (e.g., my house, brick house, hovel). Each idea of a type of house consists of ideas of various components and functions (doors, windows, shelter), which can in turn be explicated in terms of certain simple ideas (walking, vision, warmth).

When I communicate a rational thought, what I do first is to show what the components of my thought are, and then to show how the components fit together. If one of the components of the final thought were to be the final thought itself, then this rational communication would be blocked by an infinite regress. To explain the thought, I would first have to explain the thought. I could not finish unless I had already finished.

In terms of rational thoughts, the Absolute is unthinkable. There is no non-circular way to reach it from below. Any real knowledge of the Absolute must be mystical, if indeed such a thing as mystical knowledge is possible.

Mathematics and philosophy do not normally have a great deal to say about the mystical way of knowing things. Mystically speaking, it is possible to experience a direct vision of the whole Mindscape. This vision cannot be rationally communicated for the reasons just outlined. Of course, it is possible to communicate mystical knowledge in an indirect way, for example, by advocating that a person prepare his or her mind through carrying out some physical or spiritual exercises. But, ultimately, mystical knowledge is attained all at once or not at all. There is no gradual path by which to build up an M that has M as one of its elements.

Even if full knowledge of the Absolute is only possible through mysticism, it is still possible and worthwhile to discuss partial knowledge of the Absolute rationally. A significant thing about the Mindscape and the other Absolutes is that they are actually infinite. Indeed, in 1887 Cantor's friend, Richard Dedekind, published a proof that the Mindscape is infinite, where Dedekind's word for Mindscape was Gedankenwelt, meaning thought-world.³¹

Dedekind's argument for the infinitude of the Mindscape was that if s is a thought, then so is "s is a possible thought," so that if s is some rational non-self-representative thought, then each member of the infinite sequence {s, s is a possible thought, s is a possible thought is a possible thought, . . .} will be in the Mindscape, which must, therefore, be infinite.

A very similar argument proves that the class of all sets is infinite. The class of all sets is normally called V, or Cantor's Absolute. We can use the Wheelie Willie sequence of sets to see that there are infinitely many different sets in V.

Dedekind modelled his argument after an argument that appears in Bernard Bolzano's Paradoxes of the Infinite (ca. 1840):

"The class of all true propositions is easily seen to be infinite. For if we fix our attention upon any truth taken at random . . ., and label it A, we find that the proposition conveyed by the words 'A is true' is distinct from the proposition A itself . . ."³²

So we can see that the Mindscape, the class of all sets, and the class of all true propositions are all infinite. Does this guarantee that infinite objects exist? Not really. For a case can be made for the pluralist claim that the Mindscape, the class of all sets, and the class of all true propositions do not exist as objects, as unities, as finished things.

In more familiar terms, it is not hard to prove that God is infinite . . . but what if you don't believe that God exists? It may seem hard to doubt that the more impersonal Absolutes -- such as "everything," or the Mindscape -- exist, but there are those who do doubt this. The issue under consideration is a version of the old philosophical problem of the One and the Many. What is being asked is whether the cosmos exists as an organic One, or merely as a Many with no essential coherence. It is certainly true that the Mindscape, for instance, does not exist as a single rational thought. For if the Mindscape is a One, then it is a member of itself, and thus can only be known through a flash of mystical vision. No rational thought is a member of itself, so no rational thought could tie the Mindscape into a One.

Normally the word "set" is restricted by definition to apply only to collections that are not members of themselves. Under this use of the word, the class V of all sets cannot be a set, for if it were, we would have a set V such that V is a member of itself. So V becomes a collection that can never be formed into a One.

Suppose that we do not believe in circular scale and assume that any physical thing is not a part or component of itself. Is the Cosmos, the collection of all physical things, a thing? If it is, then it has to be a component of itself, which we do not allow. So the Cosmos is not a thing, but only a Many that can never be a One.

There is a highly relevant passage in a letter Cantor wrote to Dedekind in 1905:

"A multiplicity can be such that the assumption that all its elements 'are together' leads to a contradiction, so that it is impossible to conceive of the multiplicity as a unity, as 'one finished thing.' Such multiplicities I call absolutely infinite or inconsistent multiplicities. As we can readily see, the 'totality of everything thinkable,' for example, is such a multiplicity . . ."³³

Again, the reason that it would be a contradiction if the collection of all rational thoughts were a rational thought T is that then T would be a member of itself, violating the rationality of T (where "rational" means non-self-representative). The upshot of all this is that God, the Mindscape, the class of all sets, and the class of all true propositions all seem to be infinite, but it is at least possible to question whether any of these Absolutes exists as a single entity. Certainly they do not exist as entities that can be fully grasped by the rational mind.

CONNECTIONS

In this section I would like to explore some of the connections between the various sorts of infinities that have been discussed.³⁴ In his 1887 essay, "Contributions to the Study of the Transfinite," Cantor quotes a passage from Aquinas's Summa and states repeatedly that in this passage appear the only two really significant objections that have ever been raised against the actual infinite.³⁵ Let us examine this quote from Aquinas here, reproducing Cantor's italics:

The existence of an actually infinite multitude is impossible. 1) For any set of things one considers must be a specific set. And sets of things are specified by the number of things in them. Now no number is infinite, for number results from counting through a set in units. So no set of things can actually be inherently unlimited, nor can it happen to be unlimited. 2) Again, every set of things existing in the world has been created, and anything created is subject to some definite purpose of its creator, for causes never act to no purpose. All created things must be subject therefore to definite enumeration. Thus even a number of things that happens to be unlimited cannot actually exist.³⁶

It seems clear that Aquinas's first point is that an infinite set can occur only if infinite numbers exist, and he does not believe that infinite numbers exist. Cantor's theory of transfinite numbers stands as the only adequate response to this objection. For many years, it was believed that the notion of actually infinite numbers was fundamentally incoherent. It was only with the birth of Cantor's theory in the late 1800s that a consistent and reasonable theory of infinite, or transfinite, numbers was developed. As Cantor remarks in his discussion of Aquinas's objection, this objection against the existence of actually infinite collections is to be met positively by exhibiting a theory of infinite numbers.

It is not so obvious what Aquinas's second point might be. It might be taken to be simply a variation on the first point. Under this reading, the first point says that any set must have a number of cardinality, but all numbers are finite; and the second point says that any set must have a purpose or significance, but any definite purpose is finite. If this is indeed Aquinas's meaning, then we can say that once again the Cantorian theory of infinite sets provides a positive rebuttal.

Aquinas's whole view of the infinite is not really tenable, for he held that God is infinite, but that no created thing is infinite. This contradicts a widely accepted principle known as the Reflection Principle. The Reflection Principle as formulated in set theory goes as follows: every conceivable property that is enjoyed by V is also enjoyed by some set. (Recall here that V is Cantor's Absolute, the class of all sets.) Philosophically it would run: every conceivable property of the Absolute is shared by some lesser entity; or, every conceivable property of the Mindscape is also a property of some possible thought.

The motivation behind the Reflection Principle is that the Absolute should be totally inconceivable. Now, if there is some conceivable property P such that the Absolute is the only thing having property P, then I can conceive of the Absolute as "the only thing with property P." The Reflection Principle prevents this from happening by asserting that whenever I conceive of some very powerful property P, then the first thing I come up with that satisfies P will not be the Absolute, but will instead be some smallish rational thought that just happens to reflect the facet of the Absolute that is expressed by saying it has property P.

Let me give an example of a Reflection Principle argument. For every thought S in the Mindscape, the thought "S is a possible thought" is also a thought in the Mindscape. By Reflection there must, therefore, be some thought W such that For every thought S in W, the thought " S is a possible thought" is also in W. This W reflects, or shares, the italicized property of the Mindscape. But note now that this W must be infinite. So an infinite thought exists.

Again, it is true that each of the Wheelie Willie sets T_n is a member of V. By the Reflection Principle there must, therefore, be some set N such that each of the Wheelie Willie sets T_n is a member of N. Therefore an infinite set N exists.

The point I wish to make is that if one accepts the existence of any of the various infinite Absolutes, then one is fairly well committed to accepting the existence of infinite thoughts and sets. For to deny the Reflection Principle is practically to assert that the Absolute can be finitely described, which is most unreasonable.

The passage from St. Augustine that I referred to earlier contains a kind of Reflection Principle argument for the reality of the set N of all natural numbers. In that passage Augustine argues that God must already know each and every natural number and that he even knows "infiniteness" in the form of all the natural numbers taken at once -- for otherwise the set of natural numbers would exhaust his abilities. God, according to Augustine, must lie beyond the set of natural numbers.

To summarize the points in this chapter:

1. The infinite normally inspires such feelings of helplessness, futility, and despair that the natural human impulse is to reject it out of hand.
2. There are, however, no conclusive proofs that everything is finite; and the question of whether or not anything infinite exists remains as an open, almost empirical problem.
3. There are various sorts of physical infinites that could actually exist: infinite time, infinitely large space, infinite dimensional space, infinitely continuous space, and infinitely divisible matter. Each of these infinites is, in principle, avoidable; whether or not our Cosmos actually does avoid infinities remains to be seen.
4. In Cantor's set theory we have a great number of infinite sets. This simple and coherent theory of the infinite provides a logical framework in which to discuss infinities. Moreover, if we feel that the things that mathematicians discuss are real, then we can conclude that actually infinite things exist.
5. Attempts to analyze the phenomenon of consciousness and self-awareness rationally appear to lead to infinite regresses. This seems to indicate that consciousness is essentially infinite.
6. The Absolute is certainly infinite. So one must either deny the reality of the Absolute or accept the existence of at least one infinity.
7. According to the Reflection Principle, once one has an infinite Absolute, one must also have many conceivable infinities as well.

PUZZLES AND PARADOXES

1. It is sometimes said that if infinitely many planets existed, then every possible planet would have to exist, including, for instance, a planet exactly like Earth, except with unicorns. Is this necessarily true?
2. Consider a very durable ceiling lamp that has an on-off pull string. Say that the string is to be pulled at noon every day, for the rest of time. If the lamp starts out off, will it be on or off after an infinite number of days have passed?
3. For each observer O, there is some fixed upper bound N_o to the number of stars that O can physically see. Therefore, for each observer the universe is finite. Does this imply that the universe is finite?
4. "I have five fingers on my left hand" means the same thing as "When I count up all the fingers on my left hand, the last number I say is five." What might "I have fingers on my left hand" mean?
5. Suppose that we find an infinite number I that is the largest possible number. But now, what about I + 1?
6. In the little-known field of "enumerative geometry," it is said that there are points on a line and ² points in a plane. There are said to be ² lines in the plane as well: "To get the correct number ² of straight lines in the plane, we must divide the number ⁴ of pairs of points in the plane by the number ² of pairs of points on a straight line."³⁷ How many circles should there be in the plane? How many ellipses?
7. Can you prove, without circularity, that seven is a finite number?
8. The universe has lasted about 10¹⁰ years since the Big Bang. There are about 3 ¥ 10⁷ seconds in a year. According to quantum mechanics, the usual conception of continuous time does not extend to intervals shorter than 5 ¥ 10^-44 seconds, so we might think of this unit as being a kind of "instant," faster than which nothing can happen. How many "instants" of time does that come to so far? Is it reasonable to argue that larger numbers, such as 10¹⁰⁰, do not yet exist?
9. Say that the space we live in is infinitely large. Consider an infinite line L contained in our space. L is infinity yards long, and L is infinity feet long. But since each yard is three feet, L is also three-times-infinity feet long. How can infinity equal three times infinity?³⁸
10. Here is an example of an infinite regress. Suppose that some person wishes to prepare a text in which every appearance of the letters "man" is replaced by the letters "woman." If this is rigidly adhered to, then "man and woman" becomes "woman and wowoman," then "wowoman and wowowoman," and so on. What do you reach in the limit?