The Mathematical Experience
Philip J. Davis
Reuben Hersh
With an Introduction by
Gian-Carlo Rota
Birkhäuser
Boston
• Basel • Stuttgart
Infinity, or the Miraculous Jar of Mathematics
MATHEMATICS, IN ONE VIEW, is the science of
infinity. Whereas the sentences "2 + 3 = 5", "1/2 + 1/3 = 5/6",
"seventy-one is a prime
number" are instances of finite mathematics, significant
mathematics is thought to emerge when the universe of its discourse is
enlarged so as to embrace the infinite. The contemporary stockpile of
mathematical objects is full of infinities. The infinite is hard to
avoid. Consider a few typical sentences: "there are an infinite
number of points on the real line."
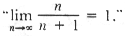
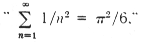
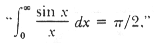
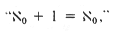
"the number of primes is
infinite," "is the number of twin primes infinite?,"
"the tape on a Turing machine is considered to be of infinite
extent," "let N be an infinite integer extracted from
the set of hyperreals." We have infinities and infinities upon
infinities; infinities galore, infinities beyond the dreams of
conceptual avarice.
The simplest of all the infinite objects is the system of positive
integers 1, 2, 3, 4, 5, . . . . The "dot dot dot" here
indicates that the list goes on forever. It never stops. This system is
commonplace and so useful that it is convenient to give it a name. Some
authors call it N (for the numbers) or Z (for
Zahlen, if they prefer a continental flavor). The set N
has the property that if a number is in it, so is its successor. Thus,
there can be no greatest number, for we can always add one and get a
still greater one. Another property that N has is that you can
never exhaust N by excluding its members one at a time. If you
delete 6 and 83 from N, what remains is an infinite set. The set
N is an inexhaustible jar, a miraculous jar recalling the miracle
of the loaves and the fishes in Matthew 15:34.
This miraculous jar with all its magical properties, properties which
appear to go against all the experiences of our finite lives, is an
absolutely basic object in mathematics, and thought to be well within
the grasp of children in the elementary schools. Mathematics asks us to
believe in this miraculous jar and we shan't get far if we don't.
It is fascinating to speculate on how the notion of the infinite
breaks into mathematics. What are its origins? The perception of great
stretches of time? The perception of great distances such as the vast
deserts of Mesopotamia or the straight line to the stars? Or could it be
the striving of the soul towards realization and perception, or the
striving towards ultimate but unrealizable explanations?
The infinite is that which is without end. It is the eternal, the
immortal, the self-renewable, the apeiron of the Greeks, the
ein-sof of the Kabbalah, the cosmic eye of the mystics which
observes us and energizes us from the godhead.
Observe the equation
1/2 + 1/4 + 1/8 + 1/16 + ... = 1,
or, in fancier notation, 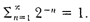 . On the
left-hand side we seem to have incompleteness, infinite striving. On the
right-hand side we have finitude, completion. There is a tension between
the two sides which is a source of power and paradox. There is an
overwhelming mathematical desire to bridge the gap between the finite
and the infinite. We want to complete the incomplete, to catch it, to
cage it, to tame it.*
Kunen describes a game in which two mathematicians with a deep
knowledge of the infinite try to outbrag each other in naming a greater
cardinal number than their opponent. Of course, one can always add one
to get a yet higher number, but the object of the game as played by
these experts is to score by breaking through with an altogether new
paradigm of cardinal formation. The playoff goes something along these
lines:
. On the
left-hand side we seem to have incompleteness, infinite striving. On the
right-hand side we have finitude, completion. There is a tension between
the two sides which is a source of power and paradox. There is an
overwhelming mathematical desire to bridge the gap between the finite
and the infinite. We want to complete the incomplete, to catch it, to
cage it, to tame it.*
Kunen describes a game in which two mathematicians with a deep
knowledge of the infinite try to outbrag each other in naming a greater
cardinal number than their opponent. Of course, one can always add one
to get a yet higher number, but the object of the game as played by
these experts is to score by breaking through with an altogether new
paradigm of cardinal formation. The playoff goes something along these
lines:
XVII
1.295.387
101010
Mathematics thinks it has succeeded in doing this. The unnamable is
named, operated on, tamed, exploited, finitized, and ultimately
trivialized. Is, then, the mathematical infinite a fraud? Does it
represent something that is not really infinite at all? Mathematics is
expressible in language that employs a finite number of symbols strung
together in sentences of finite length. Some of these sentences seem to
express facts about the infinite. Is this a mere trick of language
wherein we simply identify certain types of sentences as speaking about
"infinite things"? When infinity has been tamed it enjoys a
symbolic life.
Cantor introduced the symbol  ("aleph
nought") for the infinite cardinal number represented by the set of
natural numbers, N. He showed that this number obeyed laws of
arithmetic quite different from those of finite numbers; for instance,
("aleph
nought") for the infinite cardinal number represented by the set of
natural numbers, N. He showed that this number obeyed laws of
arithmetic quite different from those of finite numbers; for instance,
 , etc.
, etc.
Now, one could easily manufacture a hand-held computer with a  button to obey these Cantorian laws. But if
button to obey these Cantorian laws. But if  has been encased algorithmically with a finite
structure, in what, then, consists its infinity? Are we dealing only
with so-called infinities? We think big and we act small. We think
infinities and we compute finitudes. This reduction, after the act, is
clear enough, but the metaphysics of the act is far from clear.
has been encased algorithmically with a finite
structure, in what, then, consists its infinity? Are we dealing only
with so-called infinities? We think big and we act small. We think
infinities and we compute finitudes. This reduction, after the act, is
clear enough, but the metaphysics of the act is far from clear.
Mathematics, then, asks us to believe in an infinite set. What does
it mean that an infinite set exists? Why should one believe it? In
formal presentation this request is institutionalized by axiomatization.
Thus, in Introduction to Set
Theory, by Hrbacek and Jech, we read on page 54:
"Axiom of Infinity. An inductive (i.e. infinite) set exists."
Compare this against the axiom of God as presented by Maimonides
(Mishneh Torah, Book 1, Chapter 1):
The basic principle of all basic principles and the pillar of all the
sciences is to realize that there is a First Being who brought every
existing thing into being.
[BAD TEXT]
The first inaccesible cardinal
The first hyper-inaccessible cardinal
The first Mahlo cardinal
The first hyper-Mahlo
The first weakly compact cardinal
The first ineffable cardinal.
Obviously it would not be cricket to name a number that doesn't
exist, and a central problem in large cardinal theory is precisely to
explicate the sense in which the above mentioned hypers and ineffables
exist.
 Exposure to the ideas of modern mathematics has led artists to
attempt to depict graphically the haunting qualities of the
infinite. DE CHIRICO. Vostalgia of
the Infinite. 1913-14? (dated 1911 on the painting) Courtesy Museum
of Modern Art
Exposure to the ideas of modern mathematics has led artists to
attempt to depict graphically the haunting qualities of the
infinite. DE CHIRICO. Vostalgia of
the Infinite. 1913-14? (dated 1911 on the painting) Courtesy Museum
of Modern Art
Mathematical axioms have the reputation of being self-evident, but it
might seem that the axioms of infinity and that of God have the same
character as far as self-evidence is concerned. Which is mathematics and
which is theology? Does this, then, lead us to the idea that an axiom is
merely a dialectical position on which to base further argumentation,
the opening move of a game without which the game cannot get
started?
Where there is power, there is danger. This is as true in mathematics
as it is in kingship. All arguments involving the infinite must be
scrutinized with especial care, for the infinite has turned out to be
the hiding place of much that is strange and paradoxical. Among the
various paradoxes that involve the infinite are Zeno's paradox of
Achilles and the tortoise, Galileo's paradox, Berkeley's paradox of the
infinitesimals (see Chapter 5, Nonstandard Analysis), a large variety of
paradoxes that involve manipulations of infinite sums or infinite
integrals, paradoxes of noncompactness. Dirac's paradox of the function
that is useful but doesn't exist, etc. From each of these paradoxes we
have learned something new about how mathematical objects behave, about
how to talk about them. From each we have extracted the venom of
contradiction and have reduced paradox to merely standard behavior in a
nonstandard environment.
The paradox of Achilles and the tortoise asserts that Achilles cannot
catch up with the tortoise, for he must first arrive at the point where
the tortoise has just left, and therefore the tortoise is always in the
lead.
 Galileo Gahlen 1564-1642
Galileo Gahlen 1564-1642
Galileo's paradox says there are as many square numbers
as there are integers and vice versa. This is exhibited in the
correspondence  . Yet, how can this be
when not every number is a square?
. Yet, how can this be
when not every number is a square?
The paradoxes of rearrangements say that the sum of an infinite
series may be changed by rearranging its terms.
For example.
0 = (1 - 1) + (1 - 1) + (1 - 1) + . . . = 1 + ( - 1 + 1) + (- 1 + 1) + . . . = 1 + 0 + 0 + . . . = 1.
Dirac's function d(x) carries the
definition

which is self-contradictory within the framework of classical
analysis.
Achilles is an instance of irrelevant parameterization:

Of course the tortoise is always ahead at the infinite sequence of
time instants t1, t2,
t3, . . . where Achilles has just managed to catch up
to where the tortoise was at the last time instant. So what? Why limit
our discussion to the convergent sequence of times t1,
t2, . . .? This is a case of the necessity of keeping
one's eye on the doughnut and not on the hole.
Galileo's paradox is regularized by observing that the phenomenon it
describes is a distinguishing characteristic of an infinite set. An
infinite set is, simply, a set which can be put into one-to-one
correspondence with a proper subset of itself. Infinite arithmetic is
simply not the same as finite arithmetic. If Cantor tells us that  is a true equation, one has no authorization
to treat
is a true equation, one has no authorization
to treat  as a finite quantity, subtract it
from both sides of the equation to arrive at the paradoxical statement 1
= 0.
as a finite quantity, subtract it
from both sides of the equation to arrive at the paradoxical statement 1
= 0.
Berkeley's paradox of the infinitesimals was first ignored, then
bypassed by phrasing all calculus in terms of limiting processes. In the
last decade it has been regularized by "nonstandard" analysis
in a way which seems to preserve the original flavor of the creators of
the calculus.
The paradoxes of rearrangement, aggregation, noncompactness are now
dealt with on a day-to-day basis by qualification and restrictions to
absolutely convergent series, absolutely convergent integrals, uniform
convergence, compact sets. The wary mathematician is hedged in, like the
slalom skier, by hundreds of flags within whose limits he must run his
course.
The Dirac paradox which postulates the existence of a function with
contradictory properties is squared away by the creation of a variety of
operational calculi such as that of Temple-Lighthill or Mikusinski or,
the most notable, Schwartz's theory of distributions (generalized
functions).
By a variety of means, then, the infinite has been harnessed and then
housebroken. But the nature of the infinite is that it is open-ended and
the necessity for further cosmetic acts will always reappear.
Further Readings. See Bibliography
B. Bolzano: D Hilbert; K. Kuhnen: L. Zippin
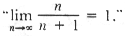
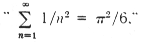
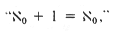
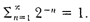 . On the
left-hand side we seem to have incompleteness, infinite striving. On the
right-hand side we have finitude, completion. There is a tension between
the two sides which is a source of power and paradox. There is an
overwhelming mathematical desire to bridge the gap between the finite
and the infinite. We want to complete the incomplete, to catch it, to
cage it, to tame it.*
Kunen describes a game in which two mathematicians with a deep
knowledge of the infinite try to outbrag each other in naming a greater
cardinal number than their opponent. Of course, one can always add one
to get a yet higher number, but the object of the game as played by
these experts is to score by breaking through with an altogether new
paradigm of cardinal formation. The playoff goes something along these
lines:
. On the
left-hand side we seem to have incompleteness, infinite striving. On the
right-hand side we have finitude, completion. There is a tension between
the two sides which is a source of power and paradox. There is an
overwhelming mathematical desire to bridge the gap between the finite
and the infinite. We want to complete the incomplete, to catch it, to
cage it, to tame it.*
Kunen describes a game in which two mathematicians with a deep
knowledge of the infinite try to outbrag each other in naming a greater
cardinal number than their opponent. Of course, one can always add one
to get a yet higher number, but the object of the game as played by
these experts is to score by breaking through with an altogether new
paradigm of cardinal formation. The playoff goes something along these
lines: ("aleph
nought") for the infinite cardinal number represented by the set of
natural numbers, N. He showed that this number obeyed laws of
arithmetic quite different from those of finite numbers; for instance,
("aleph
nought") for the infinite cardinal number represented by the set of
natural numbers, N. He showed that this number obeyed laws of
arithmetic quite different from those of finite numbers; for instance,
 , etc.
, etc. Exposure to the ideas of modern mathematics has led artists to
attempt to depict graphically the haunting qualities of the
infinite. DE CHIRICO. Vostalgia of
the Infinite. 1913-14? (dated 1911 on the painting) Courtesy Museum
of Modern Art
Exposure to the ideas of modern mathematics has led artists to
attempt to depict graphically the haunting qualities of the
infinite. DE CHIRICO. Vostalgia of
the Infinite. 1913-14? (dated 1911 on the painting) Courtesy Museum
of Modern Art Galileo Gahlen 1564-1642
Galileo Gahlen 1564-1642
 . Yet, how can this be
when not every number is a square?
. Yet, how can this be
when not every number is a square?

 is a true equation, one has no authorization
to treat
is a true equation, one has no authorization
to treat