Mathematical Models, Computers, and Platonism

AS OUR NEXT example, we consider a situation which is very typical; almost a standard situation in applied mathematics.

A mathematician is interested in the solution of a certain differential equation. He knows that this solution u(t) "exists," because standard "existence theorems" on differential equations include his problem.

Knowing that the solution exists, he proceeds to try to find out as much as he can about it. Suppose, for example, that his general theorem tells him that his function u(t) exists uniquely for all t 0. His goal is to tabulate the function u(t) as accurately as he can, especially for t close to zero and for t very large (or, as he would say, near infinity).

For t close to zero he uses something called the "Taylor series." He knows a rigorous proof that (for t small) this series converges to the solution of the equation. However, he has no way of proving how many terms of the series he must take in order to get his desired accuracy -- say, to within 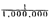of the exact value. He adds terms until he finds that the sum is unchanged by adding more terms. At that point he stops. He is guided by common sense, not by rigorous logic. He cannot prove that the neglected high-order terms are, in fact, negligible. On the other hand, he has to stop eventually. So, lacking a completely rigorous argument, he uses a plausible one to make the decision.

For t of moderate size -- neither very small nor very large -- he calculates u(t) by a recursion scheme, which replaces the differential equation by a succession of algebraic equations. He has great confidence in the accuracy of the result because he is using a differential-equation-solving program that is the most advanced of all available. It has been refined and tested for many years, and is in use in scientific laboratories all over the world. However, there is no rigorous logical proof that the numbers he gets from the machine are correct. First of all, the computing algorithm at the heart of the program cannot be guaranteed to work in all cases -- only in all "reasonable" cases. That is to say, the proof that justifies the use of this algorithm assumes that the solution has certain desirable properties which are present "normally" in "problems that usually come up." But there is nothing to guarantee this. What if he has an abnormal problem? This abnormality is usually manifested by the calculations breaking down. The numbers "blow up" -- become too big for the program to handle -- and the program stops running and warns the operator. Undoubtedly, some sufficiently clever person could cook up a differential equation to which this particular program would give reasonable-looking wrong answers.

Moreover, even if the algorithm were rigorously proved to be reliable in our case, the actual machine computation involves both software and hardware. By the "software" we mean the computer program and the whole complex of programmed control systems that permit us to write our programs in ten pages instead of a thousand. By the "hardware" is meant the machine itself, the transistors, memory, wires, and so on.

Software is itself a kind of mathematics. One could demand a rigorous proof that the software does what it is supposed to do. An area is even developing in computer science to provide "proofs of programs." As one might expect, it takes much longer to produce a proof of correctness of the program than to produce the program itself. In the case of the huge compilers that are used in large-scale scientific programming, there is no promised date for the appearance of proofs of correctness; if they ever appear, it is hard to imagine who would read the proofs and check their correctness. In the meantime, compilers are used without hesitation. Why? Because they were created by people who were doing their best to make them work correctly; because they have been in use for years, and one presumes there has been time for most of the errors to have been detected and corrected. One hopes that those that remain are harmless. If one wants to be particularly careful, one can do the computation twice, using two different systems programs, on two different machines.

As to the hardware, it usually works properly; one assumes that it is highly reliable, and the probability of failure of any one part is negligible (not zero!). Of course, there are very many parts, and it is possible that several could fail. If this happens and the computation is affected, one expects this gross misbehavior to be detected and the computer shut down for repair. But all this is only a matter of likelihood, not certainty.

Finally, what about the function u(t) for large t, "near infinity"? Computing with a machine recursively, we can go up to some large value of t, but, no matter how large, it is still finite. To finish the study of u(t), letting t approach infinity, it is often possible to use special methods of calculation, so-called "asvmptotic methods" which increase in accuracy as t gets larger. Sometimes these methods can be justified rigorously: but they are used often in the absence of such rigorous proof, on the basis of general experience and with an eye on the results to see if they "look reasonable."

If two different methods of asymptotic calculations can be carried out and the results agree, this result is considered to be almost conclusive, even though neither one has been proved correct in a rigorous mathematical sense.

Now, from the viewpoint of the formalist (our imaginary strict, extreme formalist) this whole procedure is sheer nonsense. At least, it isn't mathematics, although maybe it can pass if we call it carpentry or plumbing. Since there are no axioms, no theorems, only "blind calculations" based on fragmentary pieces of arguments, our formalist, if he is true to his philosophy, can only smile pityingly at the foolish and nonsensical work of so-called applied mathematics.

(We must beware here of a verbal trap, caused by the double meaning of the word formalism. Within mathematics itself, formalism often means calculations carried out without error estimates or convergence proofs. In this sense, the numerical and asymptotic methods used in applied mathematics are formal. But in a philosophical context, formalism means the reduction of mathematics to formal deductions from axioms, without regard to meaning.)

Philosophically, the applied mathematician is an uncritical Platonist. He takes for granted that there is a function u(t), and that he has a right to use any method he can think of to learn as much as he can about it. He would be puzzled if asked to explain where it exists or how it exists; but he knows that what he is doing makes sense. It has an inner coherence, and an interconnection with many aspects of mathematics and engineering. If the function u(t) which he attempts to compute, by one means or another -- does not exist prior to his computations, and independently of them -- then his whole enterprise, to compute it, is futile nonsense, like trying to photograph the ectoplasm at a séance.

In many instances, the differential equation whose solution he calculates is proposed as a model for some physical situation. Then, of course, the ultimate test of its utility or validity comes in its predictive or explanatory value to that physical problem. Hence, one must compare these two entities, each of which has its own objective properties -- the mathematical model, given in our example by a differential equation, and the physical model.

The physical model does not correspond exactly to an actual physical object, an observable thing in a particular time and place. It is an idealization or simplification. In any particular time and place, there are infinitely many different kinds of observations or measurements that could be asked for. What is going on at a particular time and place can always be distinguished from what is going on at some other time and place. In order to develop a theory, an understanding with some general applicability, the physicist singles out a few particular features as "state-variables" and uses them to represent the actual infinitely complex physical object. In this way he creates a physical model -- something which is already a simplification of the physical reality. This physical model, being part of a physical theory, is believed or conjectured to obey some mathematical laws. These laws or equations then specify some mathematical objects, the solutions of the mathematics equation — and these solutions are the mathematical model. Often the mathematical model one first writes down is too complicated to yield useful information, and so one introduces certain simplifications, "neglecting small terms in the equation," obtaining ultimately a simplified mathematical model which it is hoped (sometimes one can even prove it!) is close in some sense to the original mathematical model.

In any case, one must decide finally whether the mathematical model gives an acceptable description of the physical model. In order to do this, each must be studied, as a distinct reality with its own properties. The study of the mathematical model is done as we have described, with rigorous mathematics as far as possible, with nonrigorous or formal mathematics as far as possible, and with machine computations of many kinds -- simulations, truncations, discretizations.

The physical model may be studied in the laboratory, if it is possible to develop it under laboratory conditions. Or if there exists in nature some approximation to it -- in the interplanetary plasma, or in deep trenches in the depth of the Atlantic -- it may be studied wherever it is best approximated. Or it may be simulated by a computing machine, if we imagine we can tell the machine enough about how our physical model would behave. In this case, we are actually comparing two different mathematical models.

The point is that the Platonic assumption that our mathematical model is a well-defined object seems essential if the whole applied mathematical project is to make any sense.

Further Readings. See Bibliography

R. DeMillo. R. Lipton and A.J. Perlis: F. Brooks, Jr.