SPACE, TIME, AND MOTION
A Philosophical Introduction
WESLEY C. SALMON
University of Arizona
UNIVERSITY OF MINNESOTA PRESS
Minneapolis
Chapter Two
A CONTEMPORARY LOOK AT ZENO'S PARADOXES
[Much of the material in this chapter has been adapted from my
Introduction in Wesley C. Salmon, ed., Zeno's Paradoxes,
copyright “ 1970, The Bobbs-Merrill Co., Inc.
By permission of the publisher.]
The intellectual heritage bequeathed to us by the ancient Greeks was
rich indeed. The science of geometry and the entire course of Western
philosophy, as we have noted, both had their beginnings with Thales.
Both enjoyed fantastic development at the hands of his early successors,
achieving a surprising degree of perfection during antiquity. During the
same period, Aristotle provided the first systematic development of
formal logic. But the fertile soil from which all of this grew also gave
rise to a series of puzzles which have challenged successive generations
of philosophers and scientists right down to the present. These are the
famous paradoxes of Zeno of Elea who flourished about 500
B.C.1
Zeno was a devoted disciple of the philosopher Parmenides, who had
held that reality consisted of one undifferentiated, unchanging
motionless whole which was devoid of any parts. Motion, change, and
plurality were, according to him, mere illusions. Not too many
philosophers could accept this view, and Parmenides was apparently the
object of some ridicule from those who disagreed. Zeno's main purpose,
it is reported, was to refute those who made fun of his master. His aim
was to show that those who believed in motion, change, and plurality
were involved in even greater absurdities. Out of perhaps forty such
puzzles that he propounded, fewer than ten have come down to us, but
they involve some very subtle difficulties. Since motion involves the
occupation of different places at different times, these
paradoxes strike at the heart of our concepts of space and time.
Bertrand Russell once remarked that "Zeno's arguments, in some
form, have afforded grounds for almost all theories of space and
time and infinity which have been constructed from his time to our
own."2
This statement was made in 1914, in an essay
which contains a penetrating analysis of the paradoxes, but as we shall
see, there were problems inherent in these puzzles that escaped even
Russell. Such difficulties, in fact, have a direct bearing upon our
foregoing discussions of space and geometry, revealing deep problems
that we have barely mentioned. Moreover, before this chapter is
finished, I shall be reporting a new Zeno-type puzzle which first came
to light during the present decade!
The following paradoxes fall into two main categories, paradoxes of
motion and paradoxes of plurality. The paradoxes of motion
are the more famous ones, and I shall begin with them.
THE PARADOXES OF MOTION
Our knowledge of the paradoxes of motion comes from Aristotle who, in
the course of his discussions, offers a paraphrase of each. Zeno's
original formulations have not survived.
- Achilles and the Tortoise. Imagine that Achilles, the
fleetest of Greek warriors, is to run a footrace against a tortoise. It
is only fair to give the tortoise a head start. Under these
circumstances, Zeno argues, Achilles can never catch up with the
tortoise, no matter how fast he runs. In order to overtake the tortoise,
Achilles must run from his starting point A to the tortoise's original
starting point T0 (see Figure 1).
While he is doing that, the tortoise will have moved ahead to T1.
Now Achilles must reach the point T1.
While Achilles is covering this new distance,
the tortoise moves still farther to T2.

FIGURE 1.
Again, Achilles must reach this new position of the tortoise. And so it
continues; whenever Achilles arrives at a point where the tortoise
was, the tortoise has already moved a bit ahead. Achilles can
narrow the gap, but he can never actually catch up with him. This is the
most famous of all of Zeno's paradoxes. It is sometimes known simply as
"The Achilles."
- The Dichotomy. This paradox comes
in two forms, progressive and regressive. According to the first,
Achilles cannot get to the end of any racecourse, tortoise or no
tortoise; indeed, he cannot even reach the original starting point
T0 of the tortoise in the
previous paradox. Zeno argues as follows. Before the runner can
cover the whole distance he must cover the first half of it (see Figure 2).

FIGURE 2.
Then he must cover the first half of the remaining distance, and so on.
In other words, he must first run one-half, then an additional
one-fourth, then an additional one-eighth, etc., always remaining
somewhere short of his goal. Hence, Zeno concludes, he can never reach
it. This is the progressive form of the paradox, and it has very nearly
the same force as Achilles and the Tortoise, the only difference being
that in the Dichotomy the goal is stationary, while in Achilles and the
Tortoise it moves, but at a speed much less than that of Achilles.
The regressive form of the Dichotomy attempts to show, worse yet, that
the runner cannot even get started. Before he can complete the full
distance, he must run half of it (see Figure 3). But before he can
complete the first half, he must run half of that, namely, the first
quarter.
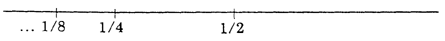
FIGURE 3.
Before he can complete the first quarter, he must run the first eighth.
And so on. In order to cover any distance no matter how short, Zeno
concludes, the runner must already have completed an infinite number of
runs. Since the sequence of runs he must already have completed has the
form of a regression,
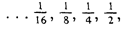
it has no first member, and hence, the runner cannot even get started.
- The Arrow. In this paradox, Zeno argues that an arrow in
flight is always at rest. At any given instant, he claims, the arrow is
where it is, occupying a portion of space equal to itself. During the
instant it cannot move, for that would require the instant to have
parts, and an instant is by definition a minimal and indivisible element
of time. If the arrow did move during the instant it would have to be in
one place at one part of the instant, and in a different place at
another part of the instant. Moreover, for the arrow to move during the
instant would require that during the instant it must occupy a space
larger than itself, for otherwise it has no room to move. As Russell
says, "It is never moving, but in some miraculous way the change of
position has to occur between the instants, that is to say, not
at any time whatever."4
This paradox is more difficult
to understand than Achilles and the Tortoise or either form of the
Dichotomy, but another remark by Russell is apt: "The more the
difficulty is meditated, the more real it becomes."
- The Stadium. Consider three rows of objects A, B, and C, arranged as in
the first position of Figure 4. Then, while row A remains at rest,
imagine rows B and C moving in opposite directions until all three rows
are lined up as shown in the second position. In the process,
C1 passes twice as many B's as A's; it lines up with the
first A to its left, but with the second B to its left. According to
Aristotle, Zeno concluded that "double the time is equal to
half."

FIGURE 4.
Some such conclusion would be warranted if we assume that the time it
takes for a C to pass to the next B is the same as the time it takes to
pass to the next A, but this assumption seems patently false. It appears
that Zeno had no appreciation of relative speed, assuming that the speed
of C relative to B is the same as the speed of C relative to A. If that
were the only foundation for the paradox we would have no reason to be
interested in it, except perhaps as a historical curiosity. It turns
out, however, that there is an interpretation of this paradox which
gives it serious import.
Suppose, as people occasionally do, that space and time are atomistic in
character, being composed of space-atoms and time-atoms of non-zero
size, rather than being composed of points and instants whose size is
zero.5
Under these circumstances, motion would consist in
taking up different discrete locations at different discrete instants.
Now, if we suppose that the A's are not moving, but the B's move to the
right at the rate of one place per instant while the C's move to the
left at the same speed, some of the C's get past some of the B's without
ever passing them. C1
begins at the right of B2
and it ends up at the left of B2,
but there is no instance at which it lines up with B2;
consequently, there is no time at which they pass each other -- it never happens.
It has been suggested that Zeno's arguments fit into an overall
pattern.6
Achilles and the Tortoise and the Dichotomy are
designed to refute the doctrine that space and time are continuous,
while the Arrow and the Stadium are intended to refute the view that
space and time have an atomic structure. The paradox of plurality, which
will be discussed later, also fits into the total schema. Thus, it has
been argued, Zeno tries to cut off all possible avenues to escape from
the conclusion that space, time, and motion are not real but
illusory.
It is extremely tempting to suppose, at first glance, that the first
three of these paradoxes at least arise from understandable confusions
on Zeno's part about concepts of the infinitesimal calculus. It was in
this spirit that the American philosopher C.S. Peirce, writing early in
the twentieth century, said of Achilles that "this ridiculous
little catch presents no difficulty at all to a mind adequately trained
in mathematics and logic."7
There is no reason to think
he regarded any of Zeno's other paradoxes more highly.
We should begin by noting that, although the calculus was developed
in the seventeenth century, its foundations were beset with very serious
logical difficulties until the nineteenth century -- when Cauchy
clarified such fundamental concepts as functions, limits, convergence of
sequences and series, the derivative, and the integral; and when his
successors Dedekind, Weierstrass, et al., provided a satisfactory
analysis of the real number system and its connections with the
calculus. I am firmly convinced that Zeno's various paradoxes
constituted insuperable difficulties for the calculus in its
pre-nineteenth-century form, but that the nineteenth-century
achievements regarding the foundations of the calculus provide means
which go far toward the resolution of Zeno's paradoxes. Let us see what
light these purified concepts can throw on the paradoxes of
motion.8
The sum of an infinite series. It is hard to guess how deep or
subtle Zeno's actual reasoning was; experts differ on the
point.9
It may have been that Zeno's original version of
Achilles and the Tortoise involved the following sort of argument: since
Achilles must traverse an infinite number of distances, each greater
than zero, in order to catch up with the tortoise, he can never do so,
for such a process would take an infinite amount of time. Against this
form of the argument Aristotle quite appropriately pointed out that the
time span during which Achilles chases after the tortoise can likewise
be subdivided into infinitely many non-zero intervals, so Achilles has
infinitely many non-zero time intervals in which to traverse the
infinitely many non-zero space intervals. But this response can hardly
be adequate, for the question still remains: how can infinitely many
positive intervals of time or space add up to anything less than
infinity? The answer to this question was not provided until Cauchy
offered a satisfactory treatment of convergent series in the first half
of the nineteenth century.
The first concept we need is the limit of an infinite
sequence. An infinite sequence is simply an ordered set of terms
{Sn}
which correspond in a one-to-one fashion with the
positive integers — each term of the sequence being coordinated by
the subscript n to a positive integer. The sequence is said to be
convergent if it has a limit. To say that such a sequence has a
limit means that there is some number L (the limit) such that the
terms of the sequence become and remain arbitrarily close to that value
as we run through the successive terms. More precisely, for any number
e greater than 0, there is some positive
integer N such that for every term Sn
with n > N, the difference between Sn and
L is less than e. In the sequence
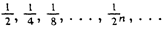
the limit is 0, since the difference between the terms of the
sequence and 0 is arbitrarily small for sufficiently large values of
n. If, for example, we choose e =
1/10, by the time we reach the fourth term S4 = 1/16,
the difference between that term and L ( = 0) is less than 1/10,
and the difference remains less than 1/10 for every subsequent member of
the sequence. For e = 1/100,
|Sn - 0| is less than
e for
n = 7, and the difference remains less than 1/100 for every
subsequent term. Similarly, e may be chosen
as small as we like, say 1/1,000,000 or 1/1,000,000,000, provided it is
greater than zero, and there is some point in this sequence beyond which
all remaining terms differ from L by less than e. It is easy to show, by completely parallel
reasoning, that the sequence
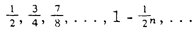
converges to the limiting value of 1.
After the concept of the limit of a sequence has been defined, it can
be used to define the sum of an infinite series. An infinite
series is simply an infinite sequence of terms which are related to one
another by addition; for example,
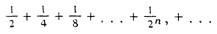
Such a sum is not defined in elementary arithmetic, for ordinary
addition is restricted to sums of finite numbers of terms, but this
operation can be extended very naturally to an infinite series. In order
to define the sum of an infinite series
s1 + s2 + s3 + ...
we form the sequence of partial sums,
S1 = s1
S2 = s1 + s2
S3 = s1 + s2 + s3
etc.
Each of these partial sums is a sum with a finite number of terms,
and it involves only the familiar operation of addition from elementary
arithmetic. We have already defined the limit of an infinite sequence.
If the sequence of partial sums,
S1, S2, S3, ...
has a limit, we say that the infinite series
s1 + s2 + s3 + ...
is convergent, and we define its sum as the limit of the sequence of
partial sums. This amounts to saying, intuitively, that the sum of a
convergent infinite series is a number that can be approximated
arbitrarily closely by adding up a sufficient (finite!) number of terms.
Given this definition of the sum of an infinite series, it becomes
perfectly meaningful to say that the infinitely many terms of a
convergent series have a finite sum.
Both the first form of the Dichotomy and the Achilles paradoxes
present us with infinite series to be summed. In the Dichotomy, for
instance, it is shown that the runner, to cover a racecourse that is one
mile in length, must cover the following series of non-overlapping
distances:
1/2 + 1/4 + 1/8 + ...
Each term of this series is greater than zero. We form the sequence
of partial sums
S1 = 1/2
S2 = 1/2 + 1/4 = 3/4
S3 = 1/2 + 1/4 + 1/8 = 7/8
etc.
As we noted above, this sequence converges to the limit 1; that is
the sum of this convergent infinite series. Achilles and the Tortoise is
quite analogous. If Achilles can run twice as fast as the tortoise, and
the tortoise has a head start of one-half of the course, the infinite
series generated by Achilles running to each subsequent starting point
of the tortoise is precisely the one we have just summed. To whatever
extent these paradoxes raised problems about the intelligibility of
adding up infinitely many positive terms, the nineteenth-century theory
of convergent sequences and series resolved the problem.
Instantaneous velocity. An intial reaction to the paradox of
the Arrow might be the suspicion that it hinges on a confusion between
the concepts of instantaneous motion and instantaneous rest, Perhaps
Zeno did feel that the only way for an arrow to be at a particular place
was to be at rest — that the notion of instantaneous non-zero
velocity was illegitimate. If Zeno argued — we have no way of
knowing whether he did or not — that at every moment of its flight
the arrow is at some place in its trajectory, and hence at every moment
of its flight it has velocity zero, then he would have been correct in
concluding that its velocity during the whole course of its flight would
be zero, rendering the arrow motionless. Nineteenth-century mathematics
showed, however, that one of these assumptions is incorrect. It is
entirely intelligible to attribute non-zero instantaneous velocities to
moving objects when an instantaneous velocity is understood as a
derivative — namely, the rate of change of position with respect
to time. This derivative is defined as the limit of the average velocity
during decreasing non-zero intervals of time. Suppose, for example, that
the arrow flies at a uniform speed. We find that in one second it covers
ten feet, in one-tenth of a second it covers one foot, in one-hundredth
of a second it covers one-tenth of a foot, and so on. As we take these
average velocities over decreasing finite time intervals which
converge to an instant t1,
the average velocities
approach a limit of ten feet per second, and this is, by definition, the
instantaneous velocity of the arrow at t1.
The same can be said for every moment during its flight; it travels its whole
course at ten feet per second, and its velocity at
each moment is
ten feet per second. If Zeno felt that the only intelligible
instantaneous velocity is zero, nineteenth-century mathematics proved
him wrong.
The infinitesimal calculus was, of course, developed in the
seventeenth century, and it made use of instantaneous velocities. These
were, unfortunately, considered to be infinitesimal distances covered in
infinitesimal times. It was against such notions that Berkeley leveled
his broadside in The Analyst,10 characterizing
infinitesimals as "ghosts of recently departed quantities." It
is possible that Zeno's Arrow paradox was also directed against just
such a conception. If we try to conceive of finite motion over a finite
distance during a finite time as being composed of a large number of
motions over infinitesimal distances during infinitesimal times,
enormous confusion is likely to ensure. How much space does an arrow
occupy during an infinitesimal time? Is it just as large as the arrow,
or is it a wee big larger? If it is larger, then how does the arrow get
from one part of that space to another? And if not, then how can the
arrow be moving at all? And how long is an infinitesimal time span? Does
it have parts or not? If so, how can we characterize motion during its
parts? If not, how can motion occur during this infinitesimal time?
These are questions that Zeno and his fellow Greeks could not answer,
and to which modern calculus prior to Cauchy had no satisfactory answer
either. This is why I remarked earlier that nineteenth-century —
not seventeenth-century — mathematics held an important key, in
the concept of the derivative, to the resolution of Zeno's Arrow
paradox.
Mathematical functions. There is, however, still an underlying
problem about instantaneous velocity. We have seen how such a concept
can be defined intelligibly, but this definition makes essential
reference to what is happening at neighboring instants. Instantaneous
velocity is defined as a limit of a sequence of average velocities over
finite time intervals; without some information about what happens in
these intervals we can say nothing about the instantaneous velocity. If
we know simply that the center of the arrow was at the point
s1 at time t1 we can draw no
conclusion whatever about its velocity at that instant. Unless we know
what the arrow was doing at other times close to t1 we
cannot distinguish instantaneous motion from instantaneous rest.
It was just this consideration, I believe, which led the philosopher
Henri Bergson to say that Zeno's Arrow paradox calls attention to the
absurd proposition ". . . that movement is made of
immobilities."11
Bergson concluded that the Arrow
paradox proves that the standard mathematical characterization of motion
must be wrong. We must look at this argument a little more closely.
In modern physics, motion is treated as a functional relationship
between points of space and instants of time. The formula for the motion
of a freely falling body, for example, is
x = f(t) = 1/2 gt2.
Such formulas make it possible, by employing the function f,
to compute the position x given a value of time t. But to
understand this treatment of motion fully, it is necessary to have a
clear conception of mathematical functions. Before the nineteenth
century there was no satisfactory treatment of functions; functions were
widely regarded as things which moved or flowed. Such a conception is of
no help in attempting to resolve Zeno's paradoxes; on the contrary,
Zeno's paradoxes of motion constitute severe difficulties for any such
notion of mathematical functions. The situation was dramatically
improved when Cauchy defined a function as simply a pairing of numbers
from one set with numbers from another set. The numbers of the first set
are the values of the argument, sometimes called the
independent variable; the numbers of the second set (which need
not be a different set) are the values of the function, sometimes
called the dependent variable. For example, the function
F(x) = y = x2
pairs real numbers
with non-negative real numbers. With the number 2 it associates the
number 4, with the number - 1 it associates the number 1, with the
number 1/2 it associates the number
1/4, and so forth. Now according to
Cauchy, the mathematical function F simply is the set of
all such pairs of numbers, namely,
x F(x) = x2
------------------------------
1 | 1
2 | 4
3 | 9
1/2 | 1/4
1/3 | 1/9
-2 | 4
-1 | 1
etc. | etc.
Similarly, the function f used to describe the motion of a
falling body is nothing more or less than a pairing of the values of the
position variable x with values of the time variable t. At
t = 0, x = 0; at t = 1, x = 16; at t
= 2, x = 64. This is how we say, in mathematical language, that a
body starting from rest in the vicinity of the surface of the earth and
falling freely travels 16 feet in the first second, 48 feet in the next
second, and so on.
Let us now apply this conception of a mathematical function to the
motion of an arrow; to keep the arithmetic simple, let it travel at the
uniform speed of ten feet per second in a straight line, starting from
x = 0 at t = 0. At any subsequent time t, its
position x = 10t. Accordingly, part of what we mean by
saying that the arrow moved from point A (x = 10) to point
B (x = 30) is simply that it was at A when t
= 1, and it was at B when t = 3. When we ask how it got
from A to B, the answer is that it occupied each of the
intervening points x (10 < x < 30) at suitable times
t (1 < t < 3) — that is, satisfying the
equation x = 10t. For example, when t = 2, the
arrow was at the point C (x = 20). When we ask how it got
from A to C, the answer is again: by occupying the
intervening positions at suitable times. Notice that this answer is
not: by zipping through the intervening points at ten feet per
second. The requirement is that the arrow be at the appropriate
point at the appropriate time — nothing is said about the
instantaneous velocity of the arrow as it occupies each of these points.
This approach has been appropriately dubbed "the at-at theory of
motion." Once the motion has been described by a mathematical
function that associates positions with times, it is then possible to
differentiate the function and find its derivative, which in turn
provides the instantaneous velocities for each moment of travel. But the
motion itself is described by the pairing of positions with times alone.
Thus, Russell was led to remark, "Weierstrass, by strictly
banishing all infinitesimals, has at last shown that we live in an
unchanging world, and that the arrow, at every moment of its flight, is
truly at rest. The only point where Zeno probably erred was in inferring
(if he did infer) that, because there is no change, therefore the world
must be in the same state at one time as at another. This consequence by
no means follows. . . ."12
What Russell is saying is basically sound, although he does perhaps
phrase it overdramatically. It is not that the arrow is "truly at
rest" during its flight; rather, the motion consists in being
at a particular point at a particular time, and regarding
each individual position at each particular moment, there is no
distinction between being at rest at the point and being in motion at
the point. The distinction between rest and motion arises only when we
consider the positions of the body at a number of different moments.
This means that, aside from being at the appropriate places at
the appropriate times, there is no additional process of
moving from one to another. In this sense, there is no absurdity
at all in supposing motion to be composed of
immobilities.13
Although this way of viewing motion is, I believe, logically
impeccable, it may be psychologically difficult to accept. Perhaps the
problem can best be seen in connection with the regressive form of the
Dichotomy paradox. Here we have Achilles at the starting point at the
very moment at which the race begins. What, we ask, must he do first?
Well, someone might say, first he has to run to the starting point of
the tortoise. But that answer cannot be correct, for before he can do
that, he must run to a point halfway between his and the tortoise's
respective starting points. Before he can do that, however, he must get
to a point halfway to the halfway point. And so on. We are off on the
infinite regress. It seems that there is no first thing for him to do;
whatever we suppose his first task to be, there another that must be
completed before he can finish it. There is, in other words, no first
interval for him to cross. This conclusion is true. But it does
not follow that Achilles cannot get started.
Consider the arrow once more. Suppose it is at point C midway
in its flight path. When we ask how it gets from C to B we
may be wondering, consciously or unconsciously, where it goes next
— how it gets to the next point. But this question is surely
illegitimate, for we are thinking of the arrow's path as a continuous
one. Since the points in a continuum are densely ordered, there is no
next point. Between any two distinct points there is another (and,
hence, infinitely many). The question about Achilles, which we just
considered in connection with the regressive Dichotomy, may arise from
the same psychological source. We may feel that his first act must be to
get to the point next to his starting point, but no such point exists.
According to the at-at theory of motion, this fact is no obstacle to
motion. Both space and time are regarded as continuous, and hence,
densely ordered. True, there is no next point of space for Achilles to
occupy, but also there is no next moment of time in which he must do so.
For each moment of time there is a corresponding point, and for each
spatial point there is a corresponding moment; nothing more is
required.
The psychological compulsion to demand a next point or a next moment
may arise from the fact that we do not experience time as a continuum of
instants without duration, but rather, as a discrete series of specious
presents, each of which lasts perhaps a few milliseconds. Aside from
anthropomorphism, however, there is no reason to try to impose the
discrete structure of psychological time upon the mathematical notion of
time as a continuum, since the continuous conception has proved itself
such an extremely fruitful tool for the description of physical
motion.14
Limits of functions. There is one final issue, arising out of
the paradoxes of motion, that was significantly clarified by
nineteenth-century foundations of mathematics. During the preceding two
centuries, while the calculus floated on vague spatial and temporal
intuitions, there was considerable controversy about the ability of a
function to reach its limit. Some functions seemed to do so; others did
not. It was all quite baffling. This puzzle relates directly to Zeno's
paradoxes of Achilles and the Tortoise and the progressive form of the
Dichotomy. Achilles seems capable of chasing the tortoise right up to
the point of overtaking him, but can he reach that limiting point?
Likewise, on the track by himself, Achilles seems capable of traversing
the various fractional parts of the course right up to the finish line,
but can he achieve that limit? Again, the definitions of functions and
limits provided in the nineteenth century come nicely to the rescue. A
limit is simply a number. A function is simply a pairing of two sets of
numbers. If the limit happens to be one of the numbers in the set of
values of the function, then the function does assume the limiting value
for some value of its argument variable. If not, then the function never
assumes the limiting value. No further question about the ability of a
function to "reach" its limit can properly arise.
There can be no serious doubt that the aforementioned
nineteenth-century mathematical developments went a long way in
resolving the problems Zeno raised about space, time, and motion. The
only question is whether there are any remaining problems associated
with the paradoxes of motion. Beginning about 1950, a number of
mathematically sophisticated writers, who were fully aware of the
foregoing considerations, felt that an important problem still remained.
One of the most articulate was Max Black, who argued that the analysis
of Achilles' attempt to catch the tortoise into an infinite sequence of
distinct runs introduces a severe logical difficulty.15
The problem, specifically, is whether it even makes sense to suppose that
anyone has completed an infinite sequence of runs. Black puts the matter
forcefully and succinctly when he says that the mathematical operation
of summing an infinite series will tell us where and when Achilles will
catch the tortoise if he can catch the tortoise at all, but that is a
big "if." There is, Black argues, a fundamental difficulty in
supposing that he can catch the tortoise, for, he maintains, "the
expression, `infinite series of acts,' is
self-contradictory."16
Black's argument is based upon consideration of a number of imaginary
machines that transfer balls from one tray to another.17
Suppose, for instance, that there are two machines, Hal and Pal, each
equipped with a tray in front. When a ball is placed in Hal's tray, he
moves it to Pal's tray; when a ball is placed in Pal's tray, he moves it
to Hal's tray. They have a sort of friendly rivalry about getting rid of
the balls. Suppose, further, that they are programmed in such a way that
each successive transfer of the ball takes a shorter time; in
particular, when the ball is first put into either tray, the machine
takes 1/2 minute to move it to the other tray, next time it takes 1/4
minute, next time 1/8 minute, and so forth. (Actually, it is more like a
frantic compulsion to get rid of the ball; they carry the maxim "It
is more blessed to give than to receive" to a ridiculous extreme.)
We begin by putting a ball in Hal's tray, and he takes 1/2 minute to
move it to Pal's tray. Pal then takes 1/2 minute to put it back in Hal's
tray, during which time Hal is resting. Then Hal takes 1/4 minute to
transfer it to Pal's tray, while Pal is resting; in the next 1/4 minute
Pal returns it to Hal's tray while Hal rests. As the process goes on,
the pace increases until we see just a blur, but at the end of two
minutes it is over, and both machines come to rest. The ball has been
transfered infinitely many times; in fact, each machine has made
infinitely many transfers (and enjoyed infinitely many rest periods)
during the two minutes.
Now, we must ask, where is the ball? Is it in Hal's tray? No, it
cannot be in Hal's tray, because every time it was put in Hal removed
it. Is it in Pal's tray? No, because every time it was put there Pal
removed it. Black concludes that the supposition that this infinite
sequence of tasks has been completed leads to an absurdity.
Another hypothetical infinity machine — perhaps the simplest
— is the Thomson lamp.18
This lamp is of a common
variety; it has a single push-button switch on its base. If the lamp is
off and you push the switch, the lamp turns on; if the lamp is on and
you push the switch, the lamp turns off. Now suppose that someone pushes
the switch an infinite number of times; he accomplishes this by
completing the first thrust in 1/2 minute, the second in 1/4 minute, the
third in 1/8 minute, much as the runner in the Dichotomy is supposed to
cover the infinite sequence of distances in decreasing times. Consider
the final state of the lamp after the infinite sequence of switchings.
Is the lamp on or off? It cannot be on, for each time it was on it was
switched off. It cannot be off, for each time it was off it was switched
on.
The speed of switching demanded is, of course, beyond human
capability, but we are concerned with logical possibilities, not
"medical" limitations. Moreover, there are mechanical
difficulties inherent in the speed required of Hal and Pal as well as
Thomson's lamp, but we are not concerned with problems of engineering.
Further, there is no use trying to evade the question by saying that the
bulb would burn out or the switch would wear out. Even if we could cover
such eventualities by technological advances, there remains a logical
problem in supposing that an infinite sequence of switching (or ball
transfers) has been achieved. The lamp must be both on and off, and
also, neither on nor off. This is a thoroughly unsatisfactory state of
affairs.
Black and Thomson are not maintaining that Achilles cannot
overtake the tortoise and finish the race. We all know that he can, and
to argue otherwise would be silly. Black is arguing that it is incorrect
to describe either feat as "completing an infinite sequence
of tasks," and Thomson draws a similar moral. They are suggesting
that the paradoxes arise because of a misdescription of the
situation.
These authors have focused upon a fundamental point. We must begin by
realizing that no definition, by itself, can provide the answer to a
physical problem. Take the simplest possible case, the familiar
definition of arithmetical addition of two terms. We find, by
experience, that it applies in some situations and not in others. If
we have m apples in one basket and n oranges in another,
then we will have m + n pieces of fruit if we put them
together in the same container. (Popular folklore notwithstanding, we
obviously can "add" apples and oranges.) However, as is well
known, if we have m quarts of alcohol in one bucket, and n
quarts of water in another, we will not have m + n quarts
of solution if we put them together in the same container. The situation
is simply another instance of the relation between pure and applied
mathematics discussed in the preceding chapter. We can define various
mathematical operations within pure mathematics, but that is no
guarantee of their applicability to the physical world. If such
operations are to be applied in the description of physical facts we
must determine empirically whether a given physical operation is an
admissible interpretation of a given mathematical operation. We have
just seen that the combining of apples and oranges in fruit baskets is a
suitable counterpart of arithmetical addition, while the mixing of
alcohol and water is not. A more significant example occurs in
Einstein's special theory of relativity, where composition of velocities
is seen not to be a physical counterpart of standard vector addition, as
we shall see in the next chapter.
The same sort of question arises when we consider applying the (now
standard) definition of the sum of an infinite series. Does a given
physical situation correspond to a particular mathematical operation, in
this case, the operation of summing an infinite series? Black concludes
that the running of a race does not correspond to the summing of an
infinite series, for the completion of an infinite sequence of tasks is
a logical impossibility. Thus, the running of a race cannot correctly be
described as completing an infinite sequence of tasks. This conclusion
has far-reaching implications for modern science. If it is right, the
usual scientific description of the racecourse as an infinitely
divisible mathematical continuum is fundamentally incorrect. It may be a
useful idealization for some purposes, but Zeno's paradoxes show that
the description cannot be literally correct. The inescapable consequence
of this view would seem to be that mathematical physics needs a
radically different mathematical foundation if it is to deal adequately
with physical reality.
Before accepting any such result, we must examine the infinity
machines more closely. They do involve difficulties, but Black and
Thomson have not identified them accurately. Consider Thomson's lamp.
(The same considerations will apply to Black's infinity machines or any
of the others.) Thomson has described a physical switching process that
occupies one minute. Given that we begin at
t0
with the lamp off, and given that a switching occurs at
t1 = 1/2,
t2 = 3/4,
and so on, we have a description that
tells, for any moment prior to the time T = 1 (that is,
one minute after t0),
whether the lamp is on or off.
For T = 1, and subsequent times, it tells us nothing. For any
time prior to T that the lamp is on, there is a subsequent time
prior to T that the lamp is off, and conversely. But this does
not imply that the lamp is both on and off at T; we can make any
supposition we like without logical conflict. We have, in effect, a
function defined over a half-open interval 0 £ t < 1, and we are asked to infer its
value at t = 1. Obviously, there is no definite answer to such a
question. If the function approached a limit at t = 1, it would
be natural to extend the definition of the function by making that limit
the value of the function at the end point. But the "switching
function" describing Thomson's lamp has no such limit, so any
extension we might choose would seem arbitrary.19
The same goes for the position of the ball Hal and Pal pass back and forth. In
the Dichotomy and the Achilles paradoxes, by contrast, the "motion
function" of the runner does approach a limit, and this limit
provides a suitably appealing answer to the question about the location
of the runner at the conclusion of his sequence of
runs.20
One cannot escape the feeling, however, that there are significant
and as yet unmentioned differences between the infinite sequence of runs
Achilles must make to catch the tortoise and the infinite sequence of
ball transfers executed by Black's machines (or the infinite sequence of
switch pushes required by the Thomson lamp). And there is at least one
absolutely crucial difference. Consider the motion of the ball as it is
passed back and forth between Hal and Pal. Say that the trays are three
inches apart. Then the ball is made to traverse this fixed
positive distance infinitely many times. In order to do so, it must
travel an infinite distance in a finite length of time. Now, no
one is interested in showing that Achilles can run an infinite distance
in a finite amount of time — he is fast, but not that fast. The
problem is to show how he can run a finite distance that can be
subdivided into an infinite number of subintervals.
Achilles can make his run if he can achieve a fixed positive
velocity; the ball which travels back and forth over the fixed distance
between Hal and Pal must achieve velocities that increase without any
bound. This difficulty could, of course, be repaired. Suppose we
stipulate that the distances covered by the ball, like the distances
Achilles must cover, decrease as the time available for each transit
decreases. This can be done by making the trays of Hal and Pal move
closer and closer during the two-minute interval, so that they coincide
in the middle at the end of the infinite sequence of transfers. But now
there is no problem at all about the position of the ball at the end
— it is right in the middle in both trays! Similar considerations
apply to the Thomson lamp. In order to accomplish a switching, the
button must be moved a certain finite distance, say 1/8 inch. If this is
done infinitely many times, the finger which pushes the button and the
button itself must traverse an infinite total distance. A necessary,
though not sufficient, condition for the convergence of an infinite
series is that the terms converge to zero. In order to overcome this
difficulty, the switch would have to be modified in some suitable way,
in which case an answer can be given to the question regarding the final
on-off state of the lamp.21
In the literature on Zeno's paradoxes of motion, especially that
concerned with the infinity machines, a good deal of emphasis has been
placed on the question of whether Achilles can be said to perform an
infinite series of distinct tasks. When we divide up the
racecourse into an infinite series of positive subintervals, it is often
claimed, we are artificially breaking up what is properly considered one
motion into infinitely many parts which — so the allegation goes
— cannot be considered as individual tasks. In order to clarify
this question, Adolf Gr¸nbaum has
given Achilles a fictitious twin — a doppelgänger —
who runs a parallel racecourse, starting and
finishing at the same time as the original Achilles.22
The new Achilles is a jerky runner. He starts out and runs the first
half of the course twice as fast as his counterpart, and then stops and
waits for him. When the slower one reaches the midpoint, the interloper
runs twice as fast to the three-quarter mark, and again waits for the
slower to catch up. He repeats the same performance for each of the
remaining infinite series of subintervals. Grünbaum calls the original Achilles, who runs smoothly from
start to finish, the legato runner; his new twin who starts and
stops is called the staccato runner. The important facts about
the staccato runner are: (1) He reaches the end of the course at the
same time as the legato runner; if the original Achilles can run the
course, so can the staccato runner. (2) The staccato runner takes a rest
of finite (non-zero) duration between each of his infinite succession of
runs; hence, there can be no question that he performs an infinite
sequence of distinct runs. (3) The staccato runner (while he is
running) runs at a fixed velocity which is
simply twice that of his
legato mate, so he is not involved in the kinds of ever-increasing
velocities that were required in the unmodified Black and Thomson
devices.
There is just one final feature of the staccato Achilles which might
be a source of worry. Although he is not required to achieve
indefinitely increasing velocities, he is required to do a lot of sudden
stopping and starting, shifting instantaneously from velocity zero to
velocity 2v (where v is the legato runner's velocity) and
back again. This clearly involves infinite accelerations — and
infinitely many of them. One could reasonably doubt the possibility of
this degree of jerkiness. It turns out, however, that even the
discontinuity in velocity is not a necessary feature of the staccato
runner. The physicist Richard Friedberg has shown, by means of a
complicated mathematical function, how to describe the motion of a more
sophisticated (and less jerky!) staccato runner who covers each
of the infinite sequence of subintervals by starting from rest,
accelerating continuously to a maximum finite velocity, decelerating
smoothly to rest, and remaining at rest for the required interval
between runs. This staccato runner executes a motion conforming to a
continuous function; his velocity (first derivative) and acceleration
(second derivative) are continuous, as are all of the higher
time-derivatives as well. Moreover, the peak velocities that occur in
the successively shorter runs also decrease, converging to zero as the
length of the run also converges to zero.23
It is hard to see
what kind of logical (or conceptual) objection can be raised against
this kind of motion. But if the sophisticated staccato runner's series
of tasks is feasible, so would be the motions of any of the
appropriately modified infinity machines. The motion of the ball passed
between Hal and Pal, for example, could be described by a combination of
two such functions — the first would describe a sequence of
motions from left to right with interspersed periods of rest; the second
would consist of a similar sequence, but with the motions from right to
left. The second set of motions would be executed during the periods of
rest granted by the first function, and the first set of motions would
occur during the rest periods granted by the second function. It
therefore appears that a suitably designed Hal-Pal pair of infinity
machines are logically possible if the legato Achilles —
the one we all granted from the beginning — can complete his
ordinary garden-variety run.
The most recent Zenoesque problem with which I am familiar is
interesting partly because its Zenonian features are not immediately
evident. It was originally published in Mathematics Magazine
(January, 1971) as a straightforward mathematical puzzle, but it was
picked up by Martin Gardner who recognized its affinities to Zeno's
paradoxes of motion. He restated it in his "Mathematical
Games" column in the Scientific American as follows:*
[Gardner's statement and my response to it is from
"Mathematical Games" by Martin Gardner, Dec. 1971. Copyright
© 1971 by Scientific American, Inc. All rights reserved.]
A boy, a girl, and a dog are at the same spot on a straight road. The
boy and the girl walk forward — the boy at four miles per hour,
the girl at three miles per hour. As they proceed the dog trots back and
forth between them at ten miles per hour. Assume that each reversal of
directions is instantaneous. An hour later, where is the dog and which
way is it facing?
Answer: The dog can be at any point between the boy and the
girl, facing either way. Proof: At the end of one hour, place the
dog anywhere between the boy and the girl, facing either direction.
Time-reverse all motions and the three will return at the same instant
to the starting point.24
Here is the response I sent in reply to a letter from Gardner:
Almost everyone has heard the old chestnut about the bird that flies
back and forth between two approaching locomotives. Say that they are 30
miles apart, that each is traveling at 15 mph, and that the bird flies
back and forth at 60 mph as they approach. How far does the bird fly
before the two engines meet? Or, to achieve historical perspective,
suppose that Achilles is pursuing the tortoise, and a Trojan fly buzzes
back and forth between them. Given a set of velocities and distances,
and our latter-day assurance that Achilles will overtake the tortoise at
a determinate time and place, we can easily figure out how far the fly
will travel. So far, we have no new Zenonian paradoxes. But, as Martin
Gardner pointed out in a recent letter, a problem due to A.K. Austin of
Sheffield University [stated above] brings up a new aspect of the old
puzzle; in fact, it is just the time reversal of the bird and train
problem.
In order to retain historical perspective, let us go back to Achilles
and the tortoise. Despite the initial handicap traditionally imposed
upon Achilles, he catches the tortoise, and to redress the grievance he
has long held against Zeno, he keeps on running, steadily increasing his
lead over the fortunate tortoise. (I consider him fortunate in this
version of the tale — at least in comparison with Lewis Carroll's
account, "What the Tortoise Said to Achilles," in which
Achilles stops and seats himself on the back of the tortoise, much to
the latter's discomfort.) But consider the Trojan fly, who attempts to
continue flying back and forth between the two runners even after the
faster overtakes the slower. When Achilles and the tortoise are just
even, the fly finds himself precisely in the position of Mr. Austin's
dog.
For the sake of definiteness, say that the tortoise travels at 1 mph,
Achilles at 5 mph (he's been running since 500 B.C., so he is not as
fleet as he once was), and the fly at 10 mph. They all arrive at the
common meeting point without difficulty. But, to paraphrase Mr.
Gardner's
comment, how can they go on? If the three start simultaneously from the
common point, the fly immediately either advances ahead of both or moves
behind both — each of which violates the condition that the fly is
always in the interval between the two (end points included). For, it
would seem we could argue [here I try to elaborate Gardner's point], in
any time interval e > 0, however small,
the tortoise travels a distance of 1 e,
Achilles covers a distance of 5 e, and the
fly goes 10 e. Hence, in an arbitrarily small
time after the meeting, the fly leaves the interval between the tortoise
and Achilles. Even if we have shown how Achilles can perform the
"supertask" of catching the tortoise, and how the tortoise can
perform the supertask of initiating his motion, it appears that the fly
now faces the new supertask of continuing to fly back and forth between
Achilles and the tortoise after the latter has been overtaken. In other
words, the fly now faces the supertask of not passing
Achilles!25
The apparent difficulty seems to me analogous to the problem pointed
out by Zeno in his regressive dichotomy paradox. There is no doubt that
the fly will outdistance both Achilles and the tortoise if he flies
steadily in one direction without turning around, even in the
arbitrarily small period of duration e. This
fact does not render the fly's motion impossible, however, for no matter
how small a time interval we choose, the fly has already reversed his
direction during that interval (infinitely many times, so he is really
quite dizzy). This simply means that there is no initial non-zero
interval during which he flies straight without reversing his direction;
thus, it does not follow that he immediately leaves the interval between
the tortoise and Achilles. In fact, we can see precisely how his rapid
reversals enable him to stay between Achilles and the tortoise after the
meeting by examining the time reversal of this motion in his approach to
the point of meeting from the earlier side. The fact that the fly does
not traverse an initial non-zero straight path is analogous to
the fact that the tortoise, in leaving his starting point, does not
traverse any initial non-zero segment of his path. The lack of a
suitable initial segment is not a serious obstacle to either of
them.
The recent literature on Zeno's paradoxes has contained a good deal
of discussion of so-called "infinity machines." These are
idealized devices that purportedly perform an infinite sequence of
tasks; they have been introduced into the discussion because of
difficulties they seem to encounter in completing the infinite sequence
of tasks (a "supertask"). The resolution of the problems
surrounding the infinity machines is strongly analogous to the
resolution of the progressive form of Zeno's dichotomy paradox. The
motion of the Trojan fly up to and including the moment Achilles
overtakes the tortoise involves exactly the same considerations. So far,
I am not aware that anyone has explicitly introduced the kind of
infinity machine that would be analogous to the regressive form of
Zeno's dichotomy paradox — a machine whose difficulty lies in
getting started with its series of tasks, in contrast with the usual
infinity machine whose difficulty lies in finishing its series of tasks.
As it turns out, our Trojan fly, in its motion from the point of meeting
of Achilles and the tortoise through the subsequent part of the run in
which Achilles is ahead of the tortoise, constitutes just such an
infinity machine (as does Austin's dog) — a regressive infinity
machine, we might say. Just as the treatment of the standard
infinity machine closely parallels the resolution of the progressive
dichotomy paradox, so does the treatment of the Trojan fly, in the
latter part of his flight, closely parallel the resolution of the
regressive dichotomy paradox.
One further problem about the motion of the fly deserves explicit
attention, namely, what is the state of motion of the fly at the precise
instant of meeting? His position is well determined; it coincides with
that of Achilles and the tortoise. The mathematical function that
describes the fly's position is a continuous function of time which
passes through the meeting point at the appropriate instant. The fly's
velocity function, on the other hand, is discontinuous. Its value is +10
when the fly is moving forward, -10 when he is moving backward, and (we
might as well say) zero when the fly meets either Achilles or the
tortoise (or both). Thus, we may appropriately assign the value zero to
the fly's velocity at the instant when all three meet. Obviously, the
velocity function has infinitely many discontinuities on each side in
the neighborhood of the point of common meeting. Each finite
discontinuity in the velocity function corresponds to an infinite
discontinuity in the acceleration, for it requires an infinite
acceleration for the fly to change velocity instantaneously from +10 to
-10 and vice versa. Moreover, as Austin's problem and its solution
shows, the state of motion of the fly (or dog) at the point of meeting
does not uniquely determine how the motion is to continue beyond that
point. In other words, although we have shown how (in some sense of
"possible") it is possible for the fly to continue his motion
through the meeting point and beyond, the motion beyond the meeting
point can be executed in infinitely many distinct ways, all of which are
consistent with the conditions imposed by the problem. To say that there
are alternative ways of performing a task does not, however, prove that
the task is impossible to execute.
In the customary formulations, Zeno's Achilles and dichotomy
paradoxes involve a finite number of discontinuities of the type just
mentioned — Achilles and the tortoise are assumed to accelerate
instantaneously at their starting points to their respective average
velocities, and to decelerate instantaneously to zero at the finish.
Similarly, most of the "infinity machines" (e.g., Black's
transferring machines, the Thomson lamp) involve infinitely many such
discontinuities clustering around some moment of termination. Using a
mathematical function supplied by Richard Friedberg, Adolf Grünbaum
has shown how such motions can be
modified so as to eliminate all of the discontinuities and still achieve
the desired total outcome. It seems reasonable to conjecture that a
similar approach could be applied to the problem of the Trojan fly (or
Austin's boy-girl-dog) in order to achieve a totally unobjectionable
description of the motion.26
Peirce to the contrary notwithstanding, the fact that Zeno's
paradoxes do pose difficulties to minds well-trained in mathematics is
attested by the large number of letters received by Mathematics
Magazine and by Martin Gardner from mathematically knowledgeable
readers claiming that in some way or other the statement of Austin's
boy-girl-dog puzzle contains an inconsistency.
A PARADOX OF PLURALITY
Although Zeno is best known for his four paradoxes of motion, he did
propound a number of other paradoxes, including one that is even more
fundamental. Although it is generally known as a paradox of
plurality, it can plausibly be construed as a geometrical paradox
which calls into question the very structure of the geometrical line (or
any other continuum). Zeno presents the argument in terms of physical
things and their parts, but the considerations he brings to bear seem to
depend only upon the fact that these things are extended — that
is, they occupy some finite, non-zero stretch of space. Although he
talks about the possibility of subdividing the parts, he is not talking
about the possibility of cutting up a physical object into separate
physical parts that can be moved away from one another. He is not
dealing with the physical hypothesis of the atomic constitution of
matter. Rather, his arguments depend upon the possibility of making
conceptual or mathematical divisions; for example, even if there are
physical atoms (or subatomic particles) that cannot be split in two, if
they occupy an extended region of space — be it ever so small
— that space can be divided in the sense that we can distinguish
its parts geometrically.
Since physical separation of parts is not at issue, we can just as
well discuss the composition of the mathematical line. Zeno's argument
runs as follows.27
As we have seen from both the Achilles and
Dichotomy paradoxes, any line segment is infinitely divisible. If we
stop short with only a finite number of divisions, it is always possible
to carry the division further. The process of halving the line, and then
halving the half, is one which has no end. Hence, if the line is made up
of parts, as it surely appears to be, then there are infinitely many of
them. Now, Zeno poses a simple dilemma. What is the size of the parts?
If they have zero magnitude, then no matter how many of them you add
together, the result will still be zero. The process of adding zeroes
never yields any answer but zero. If, however, the parts have a positive
non-zero size, then the sum of the infinite collection of them will be
infinite. In other words, a line segment must have a length of either
zero or infinity; a line segment one inch or one mile long is
impossible.
An immediate objection might be raised against the claim that the
whole must have an infinite magnitude if the parts have non-zero
size, since our discussion of the Achilles and the Dichotomy
paradoxes showed how it is entirely possible for an infinite series of
positive terms to have a finite sum. But this response is inappropriate
here. In order for an infinite series of positive terms to converge, it
is necessary that there be no smallest term; the sequence of terms must
converge to zero. This condition clearly rules out the possibility of
convergence for an infinite series of positive terms all of which are
equal to one another. In the Achilles and the Dichotomy paradoxes we
could rest content with the division of a line segment into unequal
parts, for we were not trying to divide it up into its ultimate parts.
It is hard to see, however, how different ultimate parts could have
different sizes. If one "ultimate" part were larger than
another, it would seem that the larger would be further subdividable,
and hence not ultimate after all. Zeno apparently saw this point quite
clearly.28
So, the second horn of the dilemma still stands:
if the (ultimate) parts have non-zero size, the whole is infinite in
extent.
Let us look, then, at the first horn. We have already investigated
the problem of adding up the infinitely many terms of an infinite
series. We form the sequence of partial sums and, if it has a limit, we
take that limit as the sum of the series. Obviously, an infinite series
whose terms are all zero will converge to zero, since every partial sum,
being a sum of a finite number of zeroes, will be equal to zero. It is
small wonder that philosophers from Aristotle to Bergson have denied
that the line is composed of points!
We have, however, left out a crucial fact. As Georg Cantor, the
father of modern set theory, discovered toward the end of the nineteenth
century, the number of points in a finite line segment is greater than
the number of positive integers. Both numbers are, of course, infinite,
but they are not equal to one another. The number of points in a finite
line segment (or in the entire infinitely long straight line) is
c (standing for continuum); the number of positive
integers is  (pronounced "aleph
null"; aleph is the first letter of the Hebrew alphabet). A set
which has the same number of elements as the set of positive integers is
said to be "denumerable" or "countably infinite."
Sets with larger numbers of members, including, of course, those with
c members, are called "non-denumerable" or
"uncountably infinite." Infinite sequences and series involve
countable sets of terms; they can be placed in one-to-one correspondence
with the positive integers. It is impossible to establish a one-to-one
correspondence between the set of positive integers and any set
containing c elements. Hence, if we try adding up a
non-denumerable number of zeroes we are stuck at the outset, since
addition is defined only for sums of finitely many terms or sums of
denumerable sets of terms. The operation of addition is not even defined
for a non-denumerable set of terms; consequently, we have no
justification for the conclusion of the first horn of the dilemma. We
have no basis whatever for saying that the sum of a
non-denumerable set of zeroes must be zero. This conclusion of
Zeno does not follow.29
(pronounced "aleph
null"; aleph is the first letter of the Hebrew alphabet). A set
which has the same number of elements as the set of positive integers is
said to be "denumerable" or "countably infinite."
Sets with larger numbers of members, including, of course, those with
c members, are called "non-denumerable" or
"uncountably infinite." Infinite sequences and series involve
countable sets of terms; they can be placed in one-to-one correspondence
with the positive integers. It is impossible to establish a one-to-one
correspondence between the set of positive integers and any set
containing c elements. Hence, if we try adding up a
non-denumerable number of zeroes we are stuck at the outset, since
addition is defined only for sums of finitely many terms or sums of
denumerable sets of terms. The operation of addition is not even defined
for a non-denumerable set of terms; consequently, we have no
justification for the conclusion of the first horn of the dilemma. We
have no basis whatever for saying that the sum of a
non-denumerable set of zeroes must be zero. This conclusion of
Zeno does not follow.29
I do not mean to say that it is impossible to extend the definition
of addition a step farther so as to make it applicable to sums of
c terms, nor to claim that if this is done the sum of c
zeroes must be other than zero. I imagine it is possible, consistently,
to define such an operation in a way that yields the answer zero for the
sum of any number of zeroes, finite, denumerable, or non-denumerable.
Nevertheless, the mathematics we have considered so far does not force
us to any such extension of the concept of addition, and for present
purposes it would obviously be unwise to adopt one, if there is any way
to avoid it.
There is a viable alternative, as Grünbaum
has shown, in modern measure theory.
30
This theory provides a generalization of the concept of length of an
interval. An interval is the set of points between two endpoints
A and B. If the interval contains both end points, it is a
closed interval [A, B]; if both end points are excluded, it is an
open interval represented as (A, B); and if only one end point is
included we have a half-open interval, either [A, B) or (A,
B]. For two fixed end points A and B, the measures
assigned to all of these intervals are equal. This accords with our
standard concept of length; the addition or removal of an end point does
not change the length of the interval. Measures, like lengths, are
additive. If an interval I is divided into two non-overlapping
subintervals I1
and I2, the measure
of I must be equal to the sum of the measures of
I1 and I
2. If A and B
are not distinct points, but are one and the same, the interval [A,
B] (which is the same interval as [A, A]) is said to be
degenerate — it is the unit set which contains only the point
A. Because measures are additive, the degenerate interval must
receive measure zero, and so must any set which contains any finite
number of points. This measure is, moreover, extended to infinite sets
of intervals, and it is said to be denumerably or countably additive.
This means that the measure of an infinite sequence of non-overlapping
intervals is equal to the sum of the measures of these intervals (where
the sum is defined in just the way we have already explained for the
summation of infinite convergent series). It is therefore possible to
assign measures to denumerably infinite sets of points, and for all such
sets the measure is zero. By a further extension, we can say that the
entire Euclidean straight line is also an interval, whose measure is
positive infinity (+  ).
).
The most direct way -- and also the standard way -- of
handling measures of point sets in a given line is to assign coordinates
to the points of the line in the usual way. To each point is assigned a
real number; the numerical difference between two coordinates is taken
to be the distance between those two points, and also the length of the
interval of which they are the end points. It is clear, for example,
that the measure of all of the points between zero and one — the
measure of the interval [0, 1] — is equal to one. Since the set of
all rational numbers is denumerable, the measure of all of the points in
that interval with rational coordinates is zero. The measure of all of
the irrational points between zero and one is, therefore, by
subtraction, one. This set, of course, is not an interval, nor is it the
union of any finite or denumerable set of intervals. It is doubtful that
we could properly refer to the "length" of any such set;
nevertheless, it does have a well-defined measure. We see that this
concept of measure is, indeed, a generalization of the concept of
length. However, not all sets of points on the line have measures; for
reasons we need not go into, some sets are not measurable, and they
receive no measure at all (which is not to say that their measure
is zero, for zero is a very definite measure).
It is important to emphasize the fact that measure theory does not
represent merely an extension of ordinary arithmetical addition
(including the summation of infinite series) to the addition of
non-denumerable sets of terms. In elementary arithmetic, if we are given
a set of terms, say 2, 3, 5, it has the unique sum 10. Given the same
set of terms again, the sum must be the same once more. In ordinary
addition, even the order of the terms does not matter, but in dealing
with infinite series the order of the terms may make a
difference.31
However, given the same infinite set of terms
in the same order, the sum must always be the same. For example, our
series
1/2 + 1/4 + 1/8 + ...
has the unique sum 1, and the infinite series
0 + 0 + 0 + ...
has the unique sum 0.
Measures do not behave in the same way. As Cantor showed, any line
segment of any length with its end points removed has precisely the same
number of points as any other, and the infinite straight line also has
the same number c. Moreover, the points composing any such open
interval or entire line have precisely the same internal ordering
amongst themselves. This can be shown by a simple diagrammatic argument
(see Figure 5). Given two line segments AB and CD of unequal length, we
may place the shorter above the longer and connect the end points of AB
and CD with lines that intersect at point P. Using P as a point of
projection, we can connect any point in
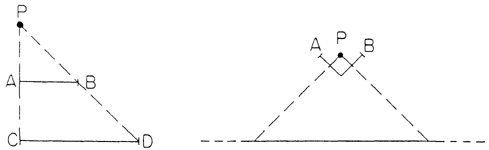 FIGURE 5.
FIGURE 5.
the open interval (AB) to a point in the open interval (CD) by a line
through P, and we can similarly connect any point in (CD) to a point in
(AB). This shows that there must be the same number of points in (AB)
and (CD), for we have just shown how to establish a one-to-one
correspondence between the members of the two sets of points. By
breaking the segment AB, we can show by similar reasoning that the open
interval (AB) has the same number of points as the infinite line.
Moreover, this correspondence between the points on the two lines is
order-preserving; that is, if two points a and b in (AB)
correspond respectively to two points c and d of (CD),
then if a is to the left of b we will find c to the
left of d. The existence of such an order-preserving one-to-one
correspondence is the defining characteristic of sameness of order; two
sets that have the same order in this precisely defined sense are said
to be isomorphic to one another. Thus, we see that every open
interval, finite or infinite, is isomorphic to every other.
It is an immediate consequence of these facts that the measure of an
interval is not uniquely determined by the number of points it contains
and the order in which they occur. Hence, if we assign each point
measure zero, and attempt to "sum" them in the order in which
they occur, we find that a given set of terms in a given order does
not determine a unique "sum." The measure of a set of
points depends upon more than the size (measure) of each of the points
and the order in which they occur.
We have just seen that point sets containing c elements could
have any finite length (measure) greater than zero, or infinite length.
We have also seen that any set of points with a finite or denumerably
infinite number of members must have zero length (measure). To prevent
the tempting misconception that the measure of a set of points is
greater than zero if and only if it has cardinality c, let us
consider Cantor's ingenious discontinuum; it contains c
points, but has measure zero. We begin with a line segment, say the set
of points between zero and one, end points included. We remove the
middle third of this line, but without taking the end points. This
leaves the closed intervals [0, 1/3] and [2/3, 1]. Next we remove the
open intervals that constitute the middle thirds of each of these
intervals, leaving four closed intervals. This process is continued
indefinitely, always removing the open middle third of each closed
interval produced in the preceding stage. Pictorially, it looks like
this:
 FIGURE 6.
FIGURE 6.
The lengths of the open intervals removed at each stage form the
following infinite series
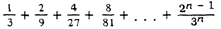
whose sum is 1. Having started with a segment with length 1, and
having removed a denumerably infinite set of open intervals whose
lengths add up to 1, we are left with a set of points having measure
zero. This set is called a discontinuum because, between any two points
remaining, at least one interval has been removed, and the remaining
points still possess the cardinality of the continuum c.
To prove that the cardinality of the remaining set is c, we
assign to each point on the segment [0, 1] its real number coordinate
value, but we express this number in ternary notation — that is,
in the notation that uses only the three digits "0,"
"1,'" and "2." In this notation, the points whose
coordinates have "0" in the first place belong to the first
third of the line, and those which have a "2" in the first
place belong to the third third. The points with a "1" in the
first place belong to the middle third, and they were removed. At the
next stage, we removed the points from the middle of the first third and
from the middle of the third third; these are the points whose
coordinates have a "1" in the second place. The successive
removals take away the points whose coordinates have "1" in
the third, fourth, fifth, and so on, places. The result of the infinite
sequence of removals is to get rid of all points that have the numeral
"1" anywhere in the
ternary expression of their
coordinates. The remaining coordinates are expressed as infinite
sequences of "0" and "2." And all possible sequences
of this description remain.
In each of these sequences, we now change every "2" to
"1." The result is a collection of sequences of "0"
and "1," and these can be interpreted as binary
representations of real numbers. Indeed, we have every possible sequence
of "0" and "1," so there is one such sequence for
each real number between zero and one. In this way we have established a
one-to-one correspondence between the points in the Cantor discontinuum
and the real numbers between zero and one. We know that this latter set
has the cardinal number c. QED.
We have found that finite or denumerably infinite sets of points
necessarily have measure zero in standard measure theory, but that sets
of points of cardinality c (if they have any measure at all) may
have measure zero, a positive finite measure, or a measure of positive
infinity. This means that having cardinality c does not in any
way determine the measure of a set of points. And we have seen,
moreover, that for segments of non-zero measure (whether finite or
infinite), there is no relation between measure and internal ordering of
points, for all open intervals, regardless of length, share the same
internal order. This means that the measure of an interval or line
segment is determined by the coordinate numbers we assign to the end
points, and not by any fact about the internal structure of the interval
or the way it is constructed out of its constituent points. These
considerations serve to resolve Zeno's "paradox of plurality,"
for they show how we can meaningfully assign non-zero finite measures to
finite intervals and segments without running into any contradiction
regarding the "addition of zeroes."
The foregoing findings enable us to shed more light on a major
problem that was discussed in the preceding chapter — namely, the
problem of ascertaining the geometrical structure of physical space. We
maintained that the answer to this question depends in an essential way
upon our interpretation of the concept of congruence of spatial
intervals. In that context we argued that various definitions of
congruence are admissible, some involving "universal forces,"
others not. At that point we called attention to a fundamental
objection. In that context we claimed that it was equally legitimate to
say that a particular measuring rod, which is not affected by any
differential forces, shrinks to half its former size as it is moved from
one place to another, or to say instead that it retains the same size
wherever it is transported. Suppose, for instance, that our measuring
rod is placed with its two ends coinciding with points A and
B. It is then moved to a different position where its ends
coincide with points C and D. We said that we are free to
stipulate that interval AB is congruent to interval CD, or
to stipulate that the length of AB equals say twice the length
CD. But, you might object, whether we know how to ascertain the
answer or not, the basic question is whether the interval AB
contains the same amount of space as the interval CD. The
answer is "yes" or "no." If it is "yes,"
then we are mistaken if we say that the rod changed its length upon
being moved. A Newtonian, for instance, would insist upon a careful
distinction between absolute space and various external devices (such as
solid bodies) that are used to investigate its structure.
The foregoing analysis of measures of the continuum provides an
answer to this Newtonian objection. We have seen that the standard
measure of an interval depends upon the coordinate numbers assigned to
its end points, not upon any intrinsic structure of the interval itself.
Thus, interval AB received the same measure as interval CD
whenever the corresponding coordinate differences were equal; otherwise,
they received a different measure. But the assignment of coordinate
numbers to points on a line is something we do by stipulation or
convention. We cannot insist that coordinate numbers be assigned in such
a way as to make equal coordinate differences coincide with equal
distances, for equal distance is defined in terms of equal
coordinate differences.
Grünbaum has summarized these
considerations by describing the geometrical continuum as
"metrically amorphous." Metrical amorphousness (as he
characterizes it) depends upon two distinct factors: (1) the arrangement
of the elements into the order type of the linear continuum, and (2) the
qualitative homogeneity or indistinguishability of the elements. The
colors, for example, can be arranged in a linear continuum, but the
different colors — the distinct hues — are not qualitatively
alike. The color continuum thus violates the second condition for
metrical amorphousness. The points of space, by contrast, do not differ
qualitatively. One might differ from another by being the site of a blue
flash, while the other is the site of a pink flash, but these are
qualitative differences between the events occurring at different
places, not differences in the points in and of themselves. Grünbaum
concludes, then, that space has no
intrinsic metric; its internal structure does not determine
distance relations.32
We establish distance relations by the
way we assign coordinates to points, or by the way we define the
geometrical congruence relation.
We now have two distinct ways of establishing distance relations, and
they might not always agree with one another. A word should be said to
clarify the relations between them. For simplicity, let us deal solely
with the relations among the points on a single line. Given such a line
(see Figure 7), let us assign coordinate numbers to its points, subject
only to the condition that the coordinate numbers satisfy the same
betweenness relations as the points to which they are assigned. In other
words, if point B lies between points A and C on
the line, then the coordinate assigned to B must be a number
between the coordinate numbers of points A and C —
for example, if B lies between A and C it would be
impermissible to assign A the coordinate 1, B the
coordinate 2, and C the coordinate 3/2. Over and above this
condition, however, the assignment of coordinates is totally arbitrary.
Both I and II (Figure 7) are acceptable ways of assigning coordinates to
the points A, B, C, D, E.
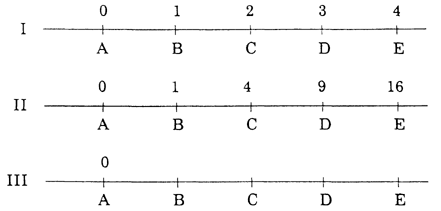 FIGURE 7.
FIGURE 7.
The next step is to decide upon a method for determining the distance
between two points when we know their coordinates; let us call such a
method a metric rule. The most obvious metric rule is the one we
employed above to assign a measure to the interval between two points:
the distance between two points is the difference between their
coordinates. Adopting this metric rule, we find that AB is
congruent to CD in system I, since 1 - 0 = 3 - 2. In system II,
using the same metric rule, these intervals are not congruent, because 1 - 0
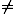 9 - 4. While it is convenient to take
the coordinate difference itself as a measure of the distance between
two points, it is not necessary to do so. One could, for instance,
define the distance as one-half of the coordinate difference, or as the
difference between the squares of the coordinates of the end points.
Using this latter rule in combination with coordinate system I is
obviously tantamount to the use of coordinate system II in conjunction
with the simpler standard metric rule. Clearly it is the combination of
coordinate system and metric rule that determines the distance relations
among the points on the line. The important fact is, given a system of
coordinates and a metric rule, all congruence relations among intervals
on the line have been determined.33
9 - 4. While it is convenient to take
the coordinate difference itself as a measure of the distance between
two points, it is not necessary to do so. One could, for instance,
define the distance as one-half of the coordinate difference, or as the
difference between the squares of the coordinates of the end points.
Using this latter rule in combination with coordinate system I is
obviously tantamount to the use of coordinate system II in conjunction
with the simpler standard metric rule. Clearly it is the combination of
coordinate system and metric rule that determines the distance relations
among the points on the line. The important fact is, given a system of
coordinates and a metric rule, all congruence relations among intervals
on the line have been determined.33
If a measuring rod is now introduced, we can ascertain empirically
how it will behave. Suppose, for example, that the end points of the rod
coincide with the points A and B, respectively, when it is
situated on that part of the line, and with the points C and
D, respectively, when it is located farther to the right. In the
coordinate system I, adopting the metric rule according to which the
length of the interval is equal to the difference of the coordinates of
the end points, the rod remains the same size in those two different
locations. Under these conditions, the rod is not subject to any
universal forces that change its size when it is transported from one of
these positions to the other. In coordinate system II, adopting the same
metric rule, the rod expands from a length of 1 to a length of 5 as it
is moved from the first position to the second. Under these conditions,
the rod is subject to universal forces which result in a change in size.
We could, of course, adopt a metric rule which equates the length of an
interval to the differences between the square roots of the coordinates
of the end points; with this rule and coordinate system II, we again
find that the rod remains the same size when it is moved from one place
to another. Which of these descriptions is correct? They are all
correct, for they are equivalent descriptions of the same situation.
There is another way to attack the same line. Instead of assigning
coordinates arbitrarily, we might use our measuring rod for this
purpose. We could choose the point A as our origin, assigning it
the coordinate 0, and mark off the intervals with our rod. Placing one
end at A, we find as a matter of fact that the other end
coincides with point B. Moving to the right, we find further that
the right end of the rod coincides with point C when the left end
is at B; moreover, the right end coincides with D when the
left end is placed on C, and so on, as shown in III (Figure 7).
Let us now stipulate that our measuring rod is free from
universal forces — that it retains the same length wherever it is
located. It follows that the intervals AB, BC, CD, DE, are all
congruent to one another. If we assign the coordinates 1 to B, 2
to C, 3 to D, and 4 to E, adopting the metric rule
which equates length with coordinate difference, we will express the
mutual congruence of these intervals. We could, of course, have chosen a
different coordinating definition, subjecting our rod to universal
forces. We could have said that it expands to three times its original
size when it is moved one position to the right, five times its original
size when it is moved to the next position to the right, seven times its
original size when it is moved to the next position, and so forth. If we
assign the coordinate 1 to B, 4 to C, 9 to D, 16 to
E, adopting the standard metric rule, we find that the intervals
AB, BC, CD, DE are all incongruent to each other. Again, we have
come up with equivalent descriptions of the same situation, both of
which are equally correct.
We have found two ways of approaching the question of length of the
intervals on a line. First, it was possible to assign coordinates
arbitrarily and choose freely among metric rules. Then the question of
whether our measuring rod stayed the same size, or changed in size, as
it was moved around — the question of whether it was subject to
universal forces — had to be settled by empirical investigation.
Second, it was possible to stipulate, via a coordinating definition,
whether the rod remained the same size or not as it was transported from
place to place. When this was done, the question of which intervals on
the line are congruent to one another had to be answered empirically.
The situation reiterates the results of our discussion of Chapter 1. We
said there that any geometrical description of the world has two
components, a specification of congruence and a geometry. Either could
be chosen freely, by stipulation; the other then became a factual matter
(at least in part). Choosing the geometry, and then investigating for
the presence or absence of universal forces, is parallel to stipulating
the coordinate system and metric rule — the first of the foregoing
two approaches. Choosing a coordinating definition of congruence, and
then ascertaining the geometrical structure of space, is parallel to the
use of the measuring rod to provide the combination of coordinate system
and metric rule. In no case, however, does the internal structure of the
line as an ordered set of points dictate its metrical structure. Its
metrical character is imposed from without by such means as choice of
coordinate system, choice of metric rule, or behavior of some sort of
measuring instrument. Our investigation of the structure of the linear
continuum thus reinforces our earlier results regarding our freedom to
select alternative definitions of congruence.
THE DISCRETE VS. THE CONTINUOUS
The infinitesimal calculus has long been — and still is —
the basic mathematical tool in the description of physical reality. It
employs variables that range over continuous sets of values, and the
functions it deals with are continuous. Although the calculus has been
completely "arithmetized," so that its formal
development does not demand any geometrical concepts, it is still
applied to phenomena that occur in physical space. Its applicability to
spatial occurrences is achieved through analytic geometry, which begins
with a one-to-one correspondence between the points on a line and the
set of real numbers. The set of real numbers constitutes a continuum in
the strict mathematical sense; consequently, the order-preserving
one-to-one correspondence between the real numbers and the points of the
geometrical line renders the line a continuum as well. If, moreover, the
geometrical line is a correct representation of lines in physical space,
then physical space is likewise continuous. Motion is treated,
moreover, as a function of a continuous time variable, and the
function itself is continuous. The continuity of the motion function is
essential, for velocity is regarded as the first derivative of such a
function, and acceleration as the second derivative. Functions which are
not continuous are not differentiable, and hence they do not even have
derivatives. Continuity is buried deep in standard mathematical physics.
It is for this reason that we have concerned ourselves at length with
the problems continuity gives rise to.34
A serious objection might be raised, however, to the view that the
mathematical continuum provides a precise and literal representation of
physical reality. Since physics customarily uses such idealizations as
frictionless planes, point-masses, and ideal gases, the argument could
go, it might be reasonable to suppose that the mathematical continuum is
another idealization that is convenient for some purposes, but does not
provide a completely accurate description of space, time, and
motion. There is, in addition, ample precedent for treating magnitudes
that are known to be discrete as if they were continuous. The law of
radioactive decay, for example, employs a continuous exponential
function even though it is universally acknowledged that the phenomenon
it describes involves discrete disintegrations of individual atoms.
Where very large finite numbers of entites are involved, the fiction of
an infinite collection is often a convenient one which yields good
approximations to what actually happens. In electromagnetic theory, for
another example, the infinitesimal calculus is used extensively in
dealing with charges, even though all the evidence points to the
quantization of charges. It has sometimes been suggested that these
considerations hold the solution to Zeno's paradoxes. For instance, the
physicist P.W. Bridgman has said, "With regard to the paradoxes of
Zeno . . . if I literally thought of a line as consisting of an
assemblage of points of zero length and of an interval of time as the
sum of moments without duration, paradox would then present
itself."35
Although I am in complete agreement with the claim that physics uses
idealizations to excellent advantage, it does not seem to me that this
provides any basis for an answer to Zeno's paradoxes of plurality or
motion. The first three paradoxes of motion purport to show a priori
that motion, if it occurs, must be discontinuous. Indeed, Zeno's
intention, as far as we can tell, seems to have been to prove a priori
that motion cannot occur. With the exception of a very few
metaphysicians of the stripe of F.H. Bradley, most philosophers would
admit that the question of whether anything moves must be answered on
the basis of empirical evidence, and that the available evidence seems
overwhelmingly to support the affirmative answer. Given that motion is a
fact of the physical world, it seems to me a further empirical question
whether it is continuous or not. It may be a very difficult and highly
theoretical question, but I do not think it can be answered a priori.
Other philosophers have disagreed. Alfred North Whitehead believed that
Zeno's paradoxes support the view that motion is atomistic in character,
while Henri Bergson seemed to hold an a priori commitment to the
continuity of motion.36
It seems to me that considerable
importance attaches to the analysis of Zeno's paradoxes for just this
reason. Space and time may, as some physicists have suggested, be
quantized, just as some other parameters, such as charge, are taken to
be.37 If this is so,
it must be a conclusion of sophisticated
physical investigation of the spatio-temporal structure of the atomic
and subatomic domains. A priori arguments, such as Zeno's paradoxes,
cannot sustain any such conclusion. The fine structure of space-time is
a matter for theoretical physics, not for a priori metaphysics,
physicists and philosophers alike notwithstanding. The result of our
attempts to resolve Zeno's paradoxes of motion is not a proof that
space, time, and motion are continuous; the conclusion is rather that
for all we can tell a priori it is an open question whether they are
continuous or not.
Before we finally leave Zeno's paradoxes, something should be said
about the view of space, time, and motion as discrete quantities. The
historical evidence suggests that some of Zeno's arguments were directed
against this alternative; that is a plausible interpretation of the
Stadium paradox at any rate. Zeno seems to have realized that, if space
and time both have discrete structure, there is a standard type of
motion that must always occur at a fixed velocity. If, for instance, an
arrow is to fly from position A to position B in as nearly
continuous a fashion as is possible in discrete space and time, then it
must occupy adjacent space atoms at adjoining atoms of time. In other
words, the standard velocity would be one atom of space per atom of
time. To travel at a lesser speed, the arrow would have to occupy at
least some of the space atoms for more than one time atom; to travel at
a greater speed, the arrow would have to skip some of the intervening
space atoms entirely, never occupying them in the course of the trip.
All of this sounds a bit strange, perhaps, but surely not logically
contradictory; this is the way the world might be. Moreover, it is
possible, as Zeno's original Stadium paradox shows, for two arrows to
pass one another traveling in opposite directions without ever being
located next to one another. Imagine two paths, located as close
together as possible in our discrete space, between A and
B. Let one arrow travel one of these paths from A to
B, while the other travels the other path from B to
A (see Figure 8). Suppose that the arrow traveling the upper
track leaves A and occupies the first square on the left, while
the arrow traveling the lower track leaves B at the same (atomic)
moment of time, occupying the first square on the right end of his path.
Let each arrow move along its track at the rate of one square for each
atom of time. At the fourth moment, the upper arrow is just to the left
of the lower arrow; at the next moment, the upper arrow is just to the
right of the lower arrow. At no moment are they side-by-side —
they get past one another, but there is no event which qualifies as the
passing (if we mean being located side-by-side traveling in the opposite
directions). This is strange perhaps, but again, it is hardly logically
impossible.
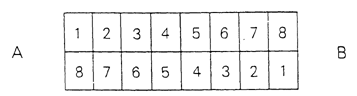 FIGURE 8.
FIGURE 8.
The mathematician Hermann Weyl has, however, posed a basic difficulty
for those who would like to quantize space.38
If we think of
a two-dimensional space as being made up of a large numbers of tiles
(something like Figure 8), we get into immediate trouble over certain
geometrical relations. Suppose for example, that we have a right
triangle ABC in such a space (see Figure 9). Consider, first,
the
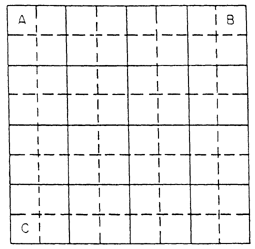 FIGURE 9.
FIGURE 9.
tiles drawn with solid lines. If the positions A, B, and
C represent the respective corner tiles, then we see that the
side AB is four units long, the side AC is four units
long, and the hypotenuse BC is also four units long. The
Pythagorean theorem says, however, that the square of the hypotenuse
equals the sum of the squares of the other two sides. This means that a
right triangle with two legs of four units each should have a hypotenuse
about 5-2/3 units long. The Pythagorean theorem is at least
approximately true in physical space, as we have found by much
experience. The result based upon tile-counting does not begin to
approximate the correct result.
This example shows something important about approximations. It is
easy to see that discontinuous motion in discrete space and time would
be difficult to distinguish from continuous motion if our space and time
atoms were small enough. It might be tempting to suppose that our
geometrical relations would approach the accustomed ones if we make our
tiles small enough. This, unfortunately, is not the case, as you can see
by taking the finer grid in Figure 9 given by the broken and solid lines
together. Instead of 16 tiles, we now have 64 tiles covering the same
region of space. But looking at our triangle ABC once more, we
see that all three sides are now 8 units long. No matter how small we
make the squares, the hypotenuse remains equal in length to the other
two sides. No wonder this is sometimes called the "Weyl tile"
argument!39
This is one case in which transition to very
small atoms does not help at all to produce the needed approximation to
the obvious features of macroscopic space. It shows the danger of
assuming that such approximation will automatically occur as we make the
divisions smaller and smaller.
It is important to resist any temptation to account for the
difficulty by saying that the diagonal distance across a tile is longer
than the breadth or height of a tile, and that we must take that
difference into account in ascertaining the length of the hypotenuse of
the triangle. Such considerations are certainly appropriate if we are
thinking of the tiles as subdivisions of a continuous background space
possessing the familiar Euclidean characteristics. But the basic idea
behind the tiles in the first place was to do away with continuous space
and replace it by discrete space. In discrete space, a space atom
constitutes one unit, and that is all there is to it. It cannot be
regarded as properly having a shape, for we cannot ascribe sizes to
parts of it — it has no parts.
Now, I do not mean to argue that there is no consistent way of
describing an atomic space or time. It would be as illegitimate to try
to prove the continuity of space and time a priori as it would be to try
to prove their discreteness a priori. But, in order to make good on the
claim that space and time are genuinely quantized, it would be necessary
to provide an adequate geometry based on these concepts. I am not
suggesting that this is impossible, but it is no routine mathematical
exercise, and I do not know that it has actually been
done.40
SUGGESTED READINGS
- Benardete, JosÈ.
Infinity; An Essay in Metaphysics. Oxford: Clarendon Press, 1964.
- Boyer, Carl B. The History of the Calculus and its Conceptual Development.
New York: Dover Publications, Inc., 1959. Previously published under the
title, The Concepts of the Calculus.
- Courant, Richard, and Robbins, Herbert. What is Mathematics?
New York: Oxford University Press, 1941.
- Gr¸nbaum, Adolf.
Modern Science and Zeno's Paradoxes.
Middletown, Conn.: Wesleyan University Press, 1967. British edition,
somewhat revised. London: George Allen & Unwin Ltd., 1968.
- Salmon, Wesley C., ed. Zeno's Paradoxes. Indianapolis: The
Bobbs-Merrill Co., 1970. An anthology containing a number of important
modern discussions and an extensive bibliography.


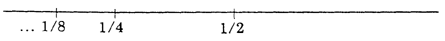

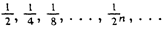
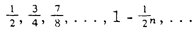
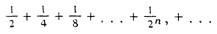
 (pronounced "aleph
null"; aleph is the first letter of the Hebrew alphabet). A set
which has the same number of elements as the set of positive integers is
said to be "denumerable" or "countably infinite."
Sets with larger numbers of members, including, of course, those with
c members, are called "non-denumerable" or
"uncountably infinite." Infinite sequences and series involve
countable sets of terms; they can be placed in one-to-one correspondence
with the positive integers. It is impossible to establish a one-to-one
correspondence between the set of positive integers and any set
containing c elements. Hence, if we try adding up a
non-denumerable number of zeroes we are stuck at the outset, since
addition is defined only for sums of finitely many terms or sums of
denumerable sets of terms. The operation of addition is not even defined
for a non-denumerable set of terms; consequently, we have no
justification for the conclusion of the first horn of the dilemma. We
have no basis whatever for saying that the sum of a
non-denumerable set of zeroes must be zero. This conclusion of
Zeno does not follow.29
(pronounced "aleph
null"; aleph is the first letter of the Hebrew alphabet). A set
which has the same number of elements as the set of positive integers is
said to be "denumerable" or "countably infinite."
Sets with larger numbers of members, including, of course, those with
c members, are called "non-denumerable" or
"uncountably infinite." Infinite sequences and series involve
countable sets of terms; they can be placed in one-to-one correspondence
with the positive integers. It is impossible to establish a one-to-one
correspondence between the set of positive integers and any set
containing c elements. Hence, if we try adding up a
non-denumerable number of zeroes we are stuck at the outset, since
addition is defined only for sums of finitely many terms or sums of
denumerable sets of terms. The operation of addition is not even defined
for a non-denumerable set of terms; consequently, we have no
justification for the conclusion of the first horn of the dilemma. We
have no basis whatever for saying that the sum of a
non-denumerable set of zeroes must be zero. This conclusion of
Zeno does not follow.29 ).
).



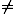 9 - 4. While it is convenient to take
the coordinate difference itself as a measure of the distance between
two points, it is not necessary to do so. One could, for instance,
define the distance as one-half of the coordinate difference, or as the
difference between the squares of the coordinates of the end points.
Using this latter rule in combination with coordinate system I is
obviously tantamount to the use of coordinate system II in conjunction
with the simpler standard metric rule. Clearly it is the combination of
coordinate system and metric rule that determines the distance relations
among the points on the line. The important fact is, given a system of
coordinates and a metric rule, all congruence relations among intervals
on the line have been determined.33
9 - 4. While it is convenient to take
the coordinate difference itself as a measure of the distance between
two points, it is not necessary to do so. One could, for instance,
define the distance as one-half of the coordinate difference, or as the
difference between the squares of the coordinates of the end points.
Using this latter rule in combination with coordinate system I is
obviously tantamount to the use of coordinate system II in conjunction
with the simpler standard metric rule. Clearly it is the combination of
coordinate system and metric rule that determines the distance relations
among the points on the line. The important fact is, given a system of
coordinates and a metric rule, all congruence relations among intervals
on the line have been determined.33
