-
I am a research associate at Dartmouth College, mathematics department with a PhD in mathematics from University of Arizona. I have interests in both pure and applied mathematics. From a theoretical point of view I do research in mathematical physics including the study of symmetries, dynamical systems and the rigorous foundation of quantum field theory. On the applied side, I work on the mathematical aspect of data science and machine learning.
Mohammad Javad Latifi
Research Associate
Dartmouth College, Department of Mathematics
Office:
Kemeny 209Research Interest:
Mathematical Physics and Geometry, Applied Mathematics and Data ScienceEmail:
mohammad.javad.latifi.jebelli@dartmouth.eduTeaching:
Math 23 - Differential Equations (Spring 2025) Math 22 - Linear Algebra (Fall 2023) Math 23 - Differential Equations (Spring 2022)Publications - Mathematical Physics and Geometry
1. Second quantization for classical nonlinear dynamics , Dimitrios Giannakis, Mohammad Javad Latifi Jebelli, Michael Montgomery, Philipp Pfeffer, Jörg Schumacher, Joanna Slawinska, 2025 (preprint). 2. The star transform, associated PDE, and real algebraic geometry, Gaik Ambartsoumian, Asher Auel, MJ Latifi, 2025 (in preparation). 3. Tensor network approximation of Koopman operators , Dimitrios Giannakis, Mohammad Javad Latifi Jebelli, Michael Montgomery, Philipp Pfeffer, Jörg Schumacher, Joanna Slawinska, 2024 (under review). 4. Kernel smoothing for discrete element models of sea ice dynamics , MJ Latifi, Dimitrios Giannakis, 2024 (under review) 5. Conversations with Flaschka: Kac–Moody groups and Verblunsky coefficients , MJ Latifi, Doug Pickrell, Physica D: Nonlinear Phenomena , Vol 445, 2023. 6. Lattice models and super telescoping formula, MJ Latifi, 2023, preprint. 7. Exponential of the S^1 trace of the free field and Verblunsky coefficients, MJ Latifi, Doug Pickrell, Rocky Mountain J. Math. 52(3), 2022. 8. Inversion and Symmetries of the Star Transform, G Ambartsoumian, MJ Latifi, The Journal of Geometric Analysis, 31 (2021), pp 11270-11291. 9. Generalized V-line transforms in 2D vector tomography, G Ambartsoumian, MJ Latifi, RK Mishra, Inverse Problems, Vol.36 (10),2020. 10. The V-line transform with some generalizations and cone differentiation, G Ambartsoumian, MJ Latifi, Inverse Problems, Vol.35 (3),2019. Publications - Applied Mathematics and Data Science
11. On the Literary Landscapes of Vector Embeddings, Daniel Rockmore, Jiayi Chen, Mohammad Javad Latifi Jebelli, Allen Riddell and Harrison Stropkay, 2024. (under review) 12. Numerical implementation of generalized V-line transforms on 2D vector fields and their inversions, MJ Latifi, Gaik Ambartsoumian, Rohit Kumar Mishra ,2023. SIAM Journal on Imaging Sciences. 13. Graph Spanners: A Tutorial Review, MJ Latifi, Reyan Ahmed, Alon Efrat, Keaton Hamm, Stephen Kobourov, Faryad Darabi Sahneh, Richard Spence, Computer Science Review, 2020. 14. Prediction of track geometry degradation using artificial neural network: a case study, MJ Latifi, Hamid Khajehei, Alireza Ahmadi, Iman Soleimanmeigouni, Mohammad Haddadzade, Arne Nissen, International Journal of Rail Transportation. 15. Approximation algorithms and an integer program for multi-level graph spanners, MJ Latifi, Reyan Ahmed, Keaton Hamm, Stephen Kobourov, FD Sahneh, Richard Spence. Analysis of Experimental Algorithms, SEA 2019. 16. A General Framework for Multi-level Subsetwise Graph Sparsifiers , MJ Latifi, Reyan Ahmed, Keaton Hamm, Stephen Kobourov, Faryad Darabi Sahneh, Richard Spence, 2019. See Google Scholar page for more.
Check out My CV.
Other
- • KSPoly: A python package I created with Dimitris Giannakis to construct smooth representation of polygonal fields using kernel operators.
- • The sound of numbers: A music page I created where users can input a sequence of numbers representing musical notes (various frequencies) and listen to sound of the sequence. The goal is to explore whether the pattern in the sequence produces a harmonious or pleasant melody.
- • Some visualizations that I made for my vector calculus students at University of Arizona.
- • A webpage where you can check the video output of the KSPoly package applied to a sea ice dataset, including the mathematical formulation.
- • Our MURI collaboration group.
Orthogonal Polynomials on \( S^1 \)
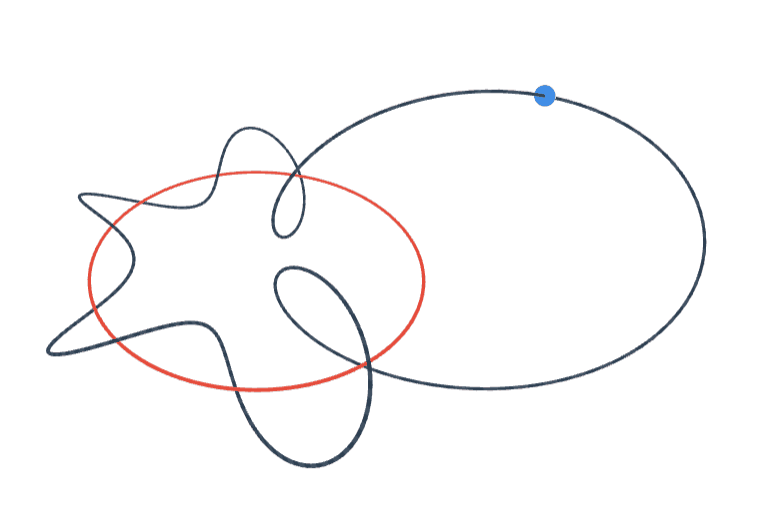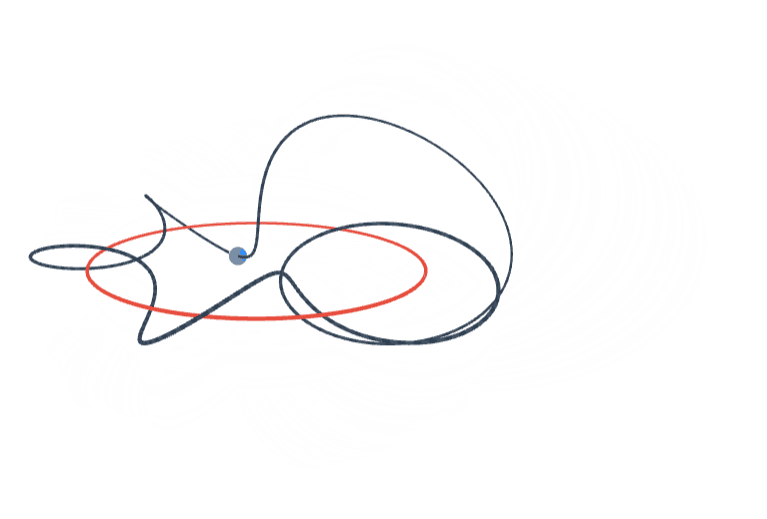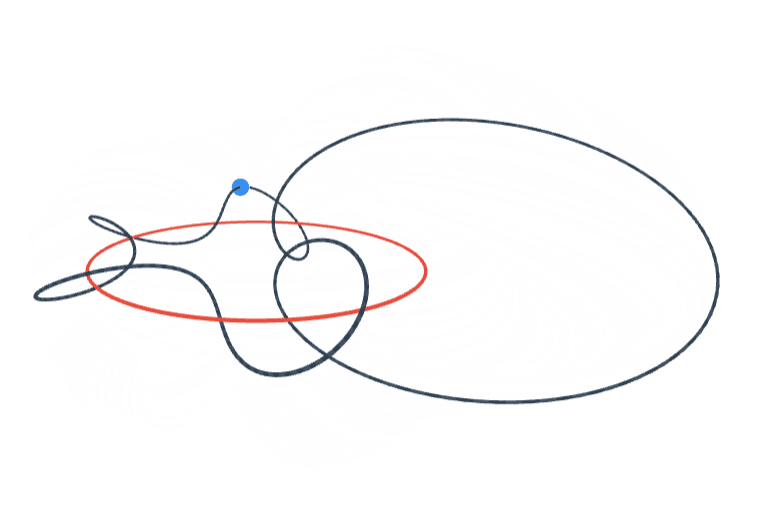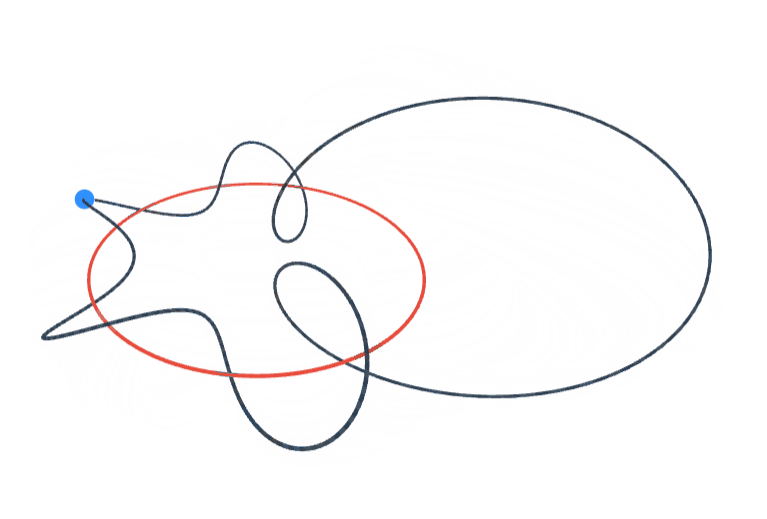
In our paper with Douglas Pickrell we introduce a new family of orthogonal polynomials on the unit circle that are associated with the family of measures \( d\mu = (1-cos \theta)^a \frac{d\theta}{2\pi} \) on \( S^1 \), parametrized with \( a>0 \). Above animation visualizes the 5th complex-valued orthogonal polynomial (degree 5) on the circle associated with \( a=1 \). See Orthogonal Polynomials on the Unit Circle: Part 1: Classical Theory by Barry Simon for a list of known examples.
Radars and Autonomous Cars at Lunewave:
The software I implemented during my time (2019) at Lunewave working on Radars and Autonomous Cars. This C++ GUI software is used for the analysis and visualization of Radar data, including algorithms to track and classify objects.