Profiles

We study the energy distribution of harmonic 1-forms on a compact hyperbolic Riemann surface \( S \) where a short closed geodesic is pinched. If the geodesic separates the surface into two parts, then the Jacobian torus of \( S \) develops into a torus that splits. If the geodesic is nonseparating then the Jacobian torus of \( S \) degenerates. The aim of this work is to get insight into this process and give estimates in terms of geometric data of both the initial surface \( S \) and the final surface, such as its injectivity radius and the lengths of geodesics that form a homology basis.
We give a general method for constructing compact Kähler manifolds \( X_1 \) and \( X_2 \) whose intermediate Jacobians \( J^k(X_1) \) and \( J^k(X_2) \) are isogenous for each \( k \), and we exhibit some examples. The method is based upon the algebraic transplantation formalism arising from Sunada's technique for constructing pairs of compact Riemannian manifolds whose Laplace spectra are the same. We also show that the method produces compact Riemannian manifolds whose Lazzeri Jacobians are isogenous.
The Jacobian of a Riemann surface and the geometry of the cut locus of simple closed geodesics

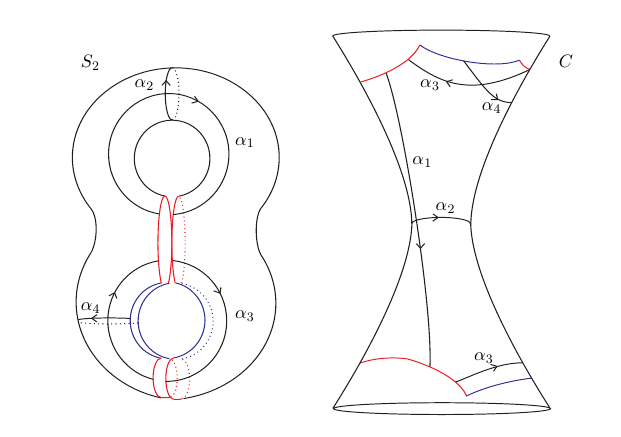
To any compact Riemann surface of genus \( g \) one may assign a principally polarized abelian variety of dimension \( g \), the Jacobian of the Riemann surface. The Jacobian is a complex torus, and a Gram matrix of the lattice of a Jacobian is called a period Gram matrix. This paper provides upper and lower bounds for all the entries of the period Gram matrix with respect to a suitable homology basis. These bounds depend on the geometry of the cut locus of non-separating simple closed geodesics. Assuming that the cut loci can be calculated, a theoretical approach is presented followed by an example where the upper bound is sharp. Finally we give practical estimates based on the Fenchel-Nielsen coordinates of surfaces of signature \( (1,1) \), or Q-pieces. The methods developed here have been applied to surfaces that contain small non-separating simple closed geodesics in \( [BMMS] \).

Let \(S\) be a translation surface of genus \(g > 1\) with \(n\) cone points \( (p_i)_{i=1,\ldots,n} \) with cone angle \( 2\pi \cdot (k_i+1)\) at \(p_i\), where \(k_i \in \mathbb{N}\). In this paper we investigate the systolic landscape of these translation surfaces for fixed genus.
Construction of hyperbolic Riemann surfaces with large systoles

Let \( S \) be a compact hyperbolic Riemann surface of genus \(g \geq 2 \). We call a systole a shortest simple closed geodesic in S and denote by \( \mathop{sys}(S) \) its length. Let \( \mathop{msys}(g) \) be the maximal value that \( \mathop{sys}(\cdot) \) can attain among the compact Riemann surfaces of genus \( g \). We call a (globally) maximal surface \( S_{max} \) a compact Riemann surface of genus \( g \) whose systole has length \( \mathop{msys}(g) \). In Section 2 we use cutting and pasting techniques to construct compact hyperbolic Riemann surfaces with large systoles from maximal surfaces. This enables us to prove several inequalities relating \( \mathop{msys}( \cdot) \) of different genera. In Section 3 we derive similar intersystolic inequalities for non-compact hyperbolic Riemann surfaces with cusps.

Let \((M,g) \) be a closed, oriented, Riemannian manifold of dimension \(m \). We call a systole a shortest non-contractible loop in \((M,g) \) and denote by \( \mathop{sys}(M,g)\) its length. Let \( \mathop{SR}(M,g)=\frac{{\mathop{sys}}^m}{\mathop{vol}(M,g)} \) be the systolic ratio of \((M,g) \). Denote by \( \mathop{SR}(k) \) the supremum of $\mathop{SR}(S,g)$ among the surfaces of fixed genus \( k \neq 0 \). In Section 2 we construct surfaces with large systolic ratio from surfaces with systolic ratio close to the optimal value \( \mathop{SR}(k) \) using cutting and pasting techniques. For all \( k_i \geq 1 \), this enables us to prove:
Quasiconformal embeddings of Y-pieces
We construct quasiconformal embeddings from Y-pieces that contain a short boundary geodesic into degenerate ones. These results are used in a companion paper to study the Jacobian tori of Riemann surfaces that contain small simple closed geodesics.
On the intersection form of surfaces

Given a closed, oriented surface \( M \), the algebraic intersection of closed curves induces a symplectic form \( \mathop{Int}(\cdot,\cdot) \) on the first homology group of \( M \). If \( M \) is equipped with a Riemannian metric \( g \), the first homology group of \( M \) inherits a norm, called the stable norm. We study the norm of the bilinear form \( \mathop{Int}(\cdot,\cdot) \), with respect to the stable norm.
Inequalities for the capacity of non-contractible annuli on cylinders of constant and variable negative curvature

We give elementary estimates for the capacity of non-contractible annuli on cylinders and provide examples, where these inequalities are sharp. Here the lower bound depends only on the area of the annulus. In the case of constant curvature this lower bound is obtained with the help of a symmetrization process that results in an annulus of minimal capacity. In the case of variable negative curvature we obtain the lower bound by constructing a comparison annulus with the same area but lower capacity on a cylinder of constant curvature. The methods developed here have been applied to estimated the energy of harmonic forms on Riemann surfaces in \( [Mu] \).
A new lower bound for Hermite's constant for symplectic lattices

In Section 1 we give an improved lower bound on Hermite's constant \( \delta_{2g} \) for symplectic lattices in even dimensions \( (g=2n) \) by applying a mean-value argument from the geometry of numbers to a subset of symmetric lattices. Here we obtain only a slight improvement. However, we believe that the method applied has further potential. In Section 2 we present new families of highly symmetric (symplectic) lattices, which occur in dimensions of powers of two. Here the lattices in dimension \( 2^n \) are constructed with the help of a multiplicative matrix group isomorphic to \( ({\mathbb{Z}_2}^n,+) \). We furthermore show the connection of these lattices with the circulant matrices and the Barnes-Wall lattices.
On the second successive minimum of the Jacobian of a Riemann surface

To a compact Riemann surface of genus \( g \) can be assigned a principally polarized abelian variety (PPAV) of dimension \( g \), the Jacobian of the Riemann surface. The Schottky problem is to discern the Jacobians among the PPAVs. Buser and Sarnak showed, that the square of the first successive minimum, the squared norm of the shortest non-zero vector in the lattice of a Jacobian of a Riemann surface of genus \( g \) is bounded from above by \( \log(4g) \), whereas it can be of order \( g \) for the lattice of a PPAV of dimension g. We show, that in the case of a hyperelliptic surface this geometric invariant is bounded from above by a constant and that for any surface of genus \( g \) the square of the second successive minimum is equally of order \( \log(g) \). We obtain improved bounds for the \(k \)-th successive minimum of the Jacobian, if the surface contains small simple closed geodesics.
Length spectrum of geodesic loops in manifolds of non-positive curvature

In Section 1 we reformulate a theorem of Blichfeldt in the framework of manifolds of non-positive curvature. As a result we obtain a lower bound on the number of homotopically distinct geodesic loops emanating from a common point \( q \) whose length is smaller than a fixed constant. This bound depends only on the volume growth of balls in the universal covering and the volume of the manifold itself. We compare the result with known results about the asymptotic growth rate of closed geodesics and loops in Section 2.
Other
In one of my previous lives I was a geneticist. The fruits of this endeavor can be found here:
FUNC: a package for detecting significant associations between gene sets and ontological annotations
published in BMC Bioinformatics.

The program package FUNC includes and expands on currently available methods to identify significant associations between gene sets and ontological annotations. Implemented are several tests in particular well suited for genome wide sequence comparisons, estimates of the family-wise error rate, the false discovery rate, a sensitive estimator of the global significance of the results and an algorithm to reduce the complexity of the results. FUNC is a versatile and useful tool for the analysis of genome-wide data. It is freely available under the GPL license and also accessible via a web service.
Regional patterns of gene expression in human and chimpanzee brains
published in Genome Research.

We have analyzed gene expression in various brain regions of humans and chimpanzees. Within both human and chimpanzee individuals, the transcriptomes of the cerebral cortex are very similar to each other and differ more between individuals than among regions within an individual. In contrast, the transcriptomes of the cerebral cortex, the caudate nucleus, and the cerebellum differ substantially from each other. Between humans and chimpanzees, 10% of genes differ in their expression in at least one region of the brain. The majority of these expression differences are shared among all brain regions. Whereas genes encoding proteins involved in signal transduction and cell differentiation differ significantly between brain regions within individuals, no such pattern is seen between the species. However, a subset of genes that show expression differences between humans and chimpanzees are distributed nonrandomly across the genome. Furthermore, genes that show an elevated expression level in humans are statistically significantly enriched in regions that are recently duplicated in humans.
A neutral model of transcriptome evolution
published in PLOS Biology.
Microarray technologies allow the identification of large numbers of expression differences within and between species. Although environmental and physiological stimuli are clearly responsible for changes in the expression levels of many genes, it is not known whether the majority of changes of gene expression fixed during evolution between species and between various tissues within a species are caused by Darwinian selection or by stochastic processes. We find the following:(1) expression differences between species accumulate approximately linearly with time;(2) gene expression variation among individuals within a species correlates positively with expression divergence between species;(3) rates of expression divergence between species do not differ significantly between intact genes and expressed pseudogenes;(4) expression differences between brain regions within a species have accumulated approximately linearly with time since these regions emerged during evolution. These results suggest that the majority of expression differences observed between species are selectively neutral or nearly neutral and likely to be of little or no functional significance. Therefore, the identification of gene expression differences between species fixed by selection should be based on null hypotheses assuming functional neutrality. Furthermore, it may be possible to apply a molecular clock based on expression differences to infer the evolutionary history of tissues.