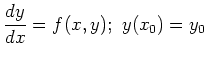A More Involved Example

Now suppose that you want to pass a function as an argument to another function. For example, you want to use Euler's method to estimate the value of the solution to the boundary value problem $${\frac{dy}{dx} = f(x,y);\ y(x_0) = y_0}$$.

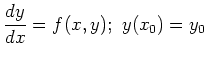Here the idea is to define a subroutine which uses the Euler method on an arbitrary function given the starting point, stepsize, and number of interations to perform.

Here is the core of the Euler subroutine

## Usage:  euler(function_reference, $x_0, $y_0, $step_size, $number_of_steps);
## Returns an array (@xcoords, @ycoords)
##
sub euler {
## Grab the parameters which were passed in the function call
    my $fn_ref = shift;   
    my $local_x0 = shift;
    my $local_y0 = shift;
    my $local_step_size = shift;
    my $local_number_of_steps = shift;

## a local variable
    my $i;

## Initialize the arrays of coordinates to return
    my @xcoords = ($local_x0);
    my @ycoords = ($local_y0);

## Perform Euler's method the requisite number of times
    for ($i = 1; $i <= $local_number_of_steps; $i++)
    {
        $xcoords[$i] = $xcoords[$i-1] + $local_step_size;
        $ycoords[$i] = $ycoords[$i-1] + 
                  $local_step_size * &$fn_ref($xcoords[$i-1], $ycoords[$i-1]);
    }

    return (@xcoords, @ycoords);
}

Next we make a function reference to pass to the Euler subroutine

## Make a function object for f(x,y) = x^2 + y^2
$f_ref = new Fun( sub {
                        my $x = shift;        ## local variable
                        my $y = shift;        ## local variable
                        return $x**2 + $y**2  ## return f(x,y)
                      } );

Finally, we invoke the Euler routine with the following syntax, the function reference being $f_ref->rule()

@x_and_y_coords = euler($f_ref->rule(),$x0,$y0,$step_size,$number_of_steps);

Note that the array which is returned has length 2*($number_of_steps + 1) with entries $x_0, x_1, \dots x_n, y_0, y_1,\dots, y_n$ where $n$ is $number_of_sreps