In drawing the above conclusions it is important to note
that symmetry effects can play a deceptive role
if the cavity shape has symmetry.
Our example Fig. 3.2a is in the ![]() symmetry group,
and the symmetry class of the deformations used are given
in Table 4.1.
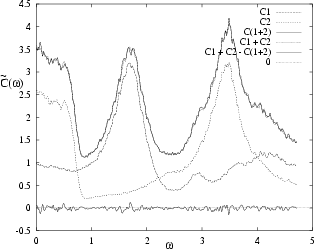
In Fig. 4.6 we demonstrate that the addition rule (4.8)
is very accurately satisfied at all
symmetry group,
and the symmetry class of the deformations used are given
in Table 4.1.
In Fig. 4.6 we demonstrate that the addition rule (4.8)
is very accurately satisfied at all ![]() if
if
![]() and
and
![]() belong to different symmetry classes of the cavity.
Orthogonality of
belong to different symmetry classes of the cavity.
Orthogonality of
![]() and
and
![]() is not sufficient to explain
this perfect linearity of addition of
is not sufficient to explain
this perfect linearity of addition of
![]() .
Rather, it follows from the symmetry of the kernel
.
Rather, it follows from the symmetry of the kernel
![]() of Eq.(3.5).
The cross-terms in (3.5) rigorously vanish
when such deformations are added, because the kernel must possess
the same symmetries are the cavity itself.
The consequence is that in order to demonstrate the
assertions of this and of the previous section,
we had to choose deformations of the same
symmetry class, or which break all symmetries of the cavity.
of Eq.(3.5).
The cross-terms in (3.5) rigorously vanish
when such deformations are added, because the kernel must possess
the same symmetries are the cavity itself.
The consequence is that in order to demonstrate the
assertions of this and of the previous section,
we had to choose deformations of the same
symmetry class, or which break all symmetries of the cavity.
 |