Introduction.

According to Dickson, Euler believed every algebraic equation was solvable by radicals [2]. The quadratic formula was know to the Babylonians; solutions of cubic and quartic polynomials by radicals were given by Scipione del Ferro, Tartaglia, Cardano and Ferrari in the mid-1500s. Abel's proof of the insolvability of the general quintic polynomial appeared in 1826 [1]; later Galois gave the exact criterion for an equation to be solvable by radicals: its Galois group must be solvable. (For a more complete historical account of the theory of equations, see van der Waerden [21], [20].)

In this paper, we consider solving equations using generally convergent purely iterative algorithms, defined by [17]. Such an algorithm assigns to its input data v a rational map , such that converges for almost all v and z; the limit point is the output of the algorithm.

This context includes the classical theory of solution by radicals, since nth roots can be reliably extracted by Newton's method.

In [11] a rigidity theorem is established that implies the maps for varying v are all conformally conjugate to a fixed model f(z). Thus the Galois theory of the output of T must be implemented by the conformal automorphism group , a finite group of Möbius transformations.

The classification of such groups is well-known: is either a cyclic group, dihedral group, or the group of symmetries of a regular tetrahedron, octahedron or icosahedron. Of these, all but the icosahedral group are solvable, leading to the necessary condition:

An equation is solvable by a tower of algorithms only if its Galois group G is nearly solvable, i.e. admits a subnormal series

such that each is either cyclic or . Incomputability of the sextic and higher polynomials follows as in ordinary Galois theory.

This necessary condition proves also sufficient; in particular, the quintic equation can be solved by a tower of algorithms.

The quintic equation and the icosahedron are of course discussed at length in Klein's treatise [8] (see also [10], [2], [5], and especially [15]). Our solution relies on the classical reduction of the quintic equation to the icosahedral equation, but replaces the transcendental inversion of the latter (due to Hermite and Kronecker) with a purely iterative algorithm.

To exhibit this method, we must construct rational maps with the symmetries of the icosahedron. It proves useful to think of a rational map f(z) on , symmetric with respect to a finite group , as a projective class of homogeneous 1-forms on , invariant with respect to the linear group . Then exterior algebra can be used to describe the space of all such maps in terms of the classical theory of invariant polynomials.

From this point of view, a rational map of degree n is canonically associated to any (n+1)-tuple of points on the sphere, and inherits the symmetries of the latter. The iterative scheme we use to solve the quintic relies on the map of degree 11 associated to the 12 vertices of the icosahedron. Its Julia set is rendered in Figure 1; every initial guess in the white region (which has full measure) converges to one of the 20 vertices of the dual dodecahedron.

  
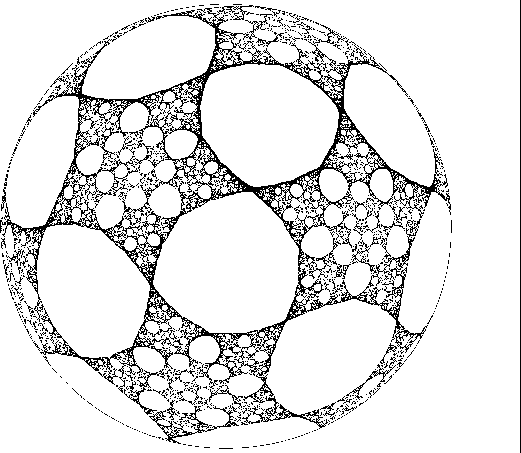
Figure 1: An icosahedral iterative scheme for solving the quintic.

Outline of the paper. §2 develops background in algebra and geometry. §3 introduces purely iterative algorithms, and §4 characterizes computable fields, given the existence of a certain symmetric rational map. §5 contains a description of all rational maps with given symmetries, which completes the proof and leads to an explicit algorithm for solving quintic equations, computed in the Appendix.

Remarks.

\

(1) Comparison should be made with the work of Shub and Smale [16] in which successful real algebraic algorithms are constructed for a wide class of problems (in particular, finding the common zeros of n polynomials in n variables with no restrictions on degree). These algorithms exhibit much of the flexibility of smooth dynamical systems (in fact they are discrete approximations to the Newton vector field).

(2) One can also consider more powerful algorithms which are still complex algebraic, e.g. by allowing more than one number to be updated during iterations. Tools for pursuing this direction (such as the theory of iterated rational functions on , n > 1) have yet to be fully developed.