Purely Iterative Algorithms.

In this section, generally convergent purely iterative algorithms are introduced and we prove that the correspondences they compute are rigid.

Definitions. An purely iterative algorithm is a rational map

carrying the input variety V into the space of of rational endomorphisms of the Riemann sphere of degree d. To avoid special considerations of `elementary rational maps', we will always assume that d is >1.

Let k denote the function field K(V); then T is simply an element of k(z).

The algorithm is generally convergent if converges for all (v,z) in an open dense subset of . (Here denotes the nth iterate of the map T).

The map can be thought of as a fixed procedure for improving the initial guess z. The output of the algorithm is described by the set

Since different w may converge to different limits, the output can be multivalued.

A family of rational maps is rigid if there is a fixed rational map f(z) such that is conjugate to f(z) for all v in a Zariski open subset of V.

T 3.1. A generally convergent algorithm is a rigid family of rational maps.

This is a consequence of the general rigidity theorem for stable algebraic families, exactly as in Theorem 1.1 of [11].

C 3.2. The output of a purely iterative algorithm is a finite union of rigid correspondences.

Proof. The output W is a finite union of components of the algebraic set ; each component is a variety. The Möbius transformation conjugating to the fixed model f(z) carries the output of to the attractor A of f, so each component is a rigid correspondence.

To make examples of generally convergent algorithms, one must check that a given iteration will converge for most initial guesses. Here is one special but useful criterion. A rational map f(z) is critically finite if every critical point c is eventually periodic (there exist n > m > 0 such that ). A periodic cycle which includes a critical point is said to be superattracting.

T 3.3. Let f(z) be a critically finite rational map, A the union of its superattracting cycles. Then either

(a)

A is empty and the action of f on is ergodic, or

(b)

A is nonempty, and tends to a cycle of A for all z in an open, full measure subset of .

In case every critical point eventually lands in A, f(z) belongs to the general class of `expanding' rational maps, for which the result is proven in [18]. The general case can be handled similarly, using orbifolds. This is sketched for polynomials by Douady and Hubbard [3]; the orbifold approach for general critically finite maps is discussed in [19].

All examples of generally convergent algorithms we will consider employ critically finite maps. In practical terms, these maps have two benefits: convergence is assured almost everywhere, not just on an open dense set; and convergence is asymptotically quadratic (for a fixed convergent initial guess, digits of accuracy are obtained in O(N) iterations).

Examples of purely iterative algorithms.

\

(1) Newton's method. Let and let . Then T is a purely iterative algorithm, and it is generally convergent for d=2 but not for d=3 or more (Figure 2; see also [17]).

  
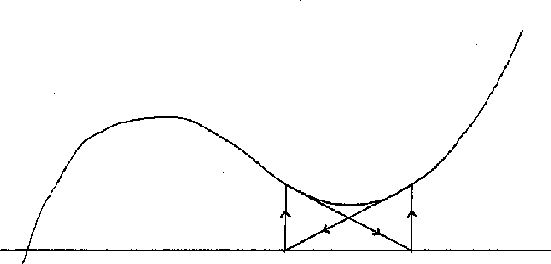
Figure 2: Newton's method can fail for cubics.

(2) Extracting radicals. Let denote the set of polynomials . The restriction of Newton's method to V is generally convergent; thus one can reliably extract radicals. The critical points of occur at the roots of p (which are fixed) and at z=0 (which maps to under one iteration, and then remains fixed); thus is critically finite, and by Theorem 3.3, almost every initial guess converges to a root.

Rigidity of the algorithm is easily verified, using the affine invariance of Newton's method.

(3) Solving the cubic. The roots of can be reliably determined by applying Newton's method to the rational function

The critical points of coincide with the roots of p, and are fixed, so again Theorem 3.3 may be applied to verify convergence.

(4) Insolvability of the quartic. Since the roots of two quartics are generally not related by a Möbius transformation (the cross-ratio of the roots must agree), the roots of polynomials of degree 4 (or more) cannot be computed by a generally convergent algorithm.

A more topological discussion of the insolvability of the quartic, using braids, appears in [12].