Kenneth P. Bogart
Peter G. Doyle
Last revised September 1985
Version 1.0A1 dated 5 September 1994
The ménage problem asks for the number of ways of seating n couples at a circular table, with men and women alternating, so that no one sits next to his or her partner. We present a straight-forward solution to this problem. What distinguishes our approach is that we do not seat the ladies first.
The ménage problem (problème des ménages) asks for the number
![]() of ways of seating n man-woman couples at a circular table,
with men and women alternating, so that no one sits next to his or
her partner. This famous problem was initially posed by Lucas
[8]
in
1891, though an equivalent problem had been raised earlier by Tait
[12]
in connection with his work on knot theory
(see Kaplansky and
Riordan
[6]).
This problem has been discussed by numerous authors
(see the references listed in
[6]),
and many solutions have been
found. Most of these solutions tell how to compute
of ways of seating n man-woman couples at a circular table,
with men and women alternating, so that no one sits next to his or
her partner. This famous problem was initially posed by Lucas
[8]
in
1891, though an equivalent problem had been raised earlier by Tait
[12]
in connection with his work on knot theory
(see Kaplansky and
Riordan
[6]).
This problem has been discussed by numerous authors
(see the references listed in
[6]),
and many solutions have been
found. Most of these solutions tell how to compute ![]() using
recurrence relations or generating functions, as opposed to giving an
explicit formula. The first explicit formula for
using
recurrence relations or generating functions, as opposed to giving an
explicit formula. The first explicit formula for ![]() , was published by
Touchard
[13]
in 1934, though he did not give a proof. Finally, in
1943, Kaplansky
[5]
gave a proof of Touchard's formula. Kaplansky's
derivation was simple but not quite straight-forward, and the
problem is still generally regarded to be tricky.
, was published by
Touchard
[13]
in 1934, though he did not give a proof. Finally, in
1943, Kaplansky
[5]
gave a proof of Touchard's formula. Kaplansky's
derivation was simple but not quite straight-forward, and the
problem is still generally regarded to be tricky.
We will present a completely straight-forward derivation of Touchard's formula. Like Kaplansky's, our solution is based on the principle of inclusion and exclusion (see Ryser [11] and Riordan [9]). What distinguishes our approach is that we do not seat the ladies (or gentlemen) first.
We begin with an apparently simpler problem, called the relaxed
ménage problem, which asks for the number ![]() of ways of seating n
couples around a circular table, so that no one sits next to his or her
partner. This is nearly the same as the ménage problem, only now we
have relaxed the requirement that men and women alternate.
of ways of seating n
couples around a circular table, so that no one sits next to his or her
partner. This is nearly the same as the ménage problem, only now we
have relaxed the requirement that men and women alternate.
To determine ![]() , we begin with the set S of all (2n)! ways of
seating the 2n individuals around the table, and use inclusion-exclusion
on the set of couples who end up sitting together. Let us
call the elements of S seatings, and let us denote by
, we begin with the set S of all (2n)! ways of
seating the 2n individuals around the table, and use inclusion-exclusion
on the set of couples who end up sitting together. Let us
call the elements of S seatings, and let us denote by ![]() the number
of seatings under which some specified set of k couples (and
possibly some other couples) end up sitting together. Clearly,
the number
of seatings under which some specified set of k couples (and
possibly some other couples) end up sitting together. Clearly, ![]() does not depend on the particular set of k couples we choose, and so,
by the principle of inclusion and exclusion, we have
does not depend on the particular set of k couples we choose, and so,
by the principle of inclusion and exclusion, we have
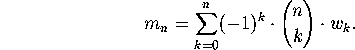
To finish the enumeration, we must compute ![]() . Assume n>1. Let
. Assume n>1. Let ![]() denote the number of ways of placing k non-overlapping unlabeled
dominos on 2n vertices arranged in a circle.
(See Figure 1.)
denote the number of ways of placing k non-overlapping unlabeled
dominos on 2n vertices arranged in a circle.
(See Figure 1.)
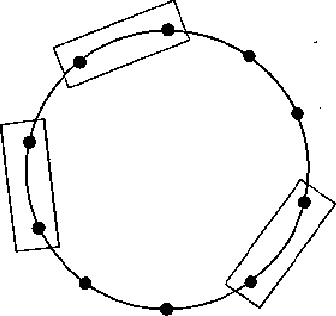
Figure 1: Non-overlapping dominos
Then
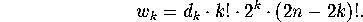
(Decide where the k couples go, and which couple goes where, and
which partner
takes which seat, and where the 2n-2k individuals go.) So now we
have only to
compute the ![]() 's. This is a routine combinatorial problem. The
answer is
's. This is a routine combinatorial problem. The
answer is
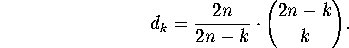
(See Ryser [11], pp. 33-34, or Exercise 1 below). This yields
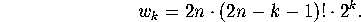
Plugging this expression for ![]() into the formula for
into the formula for ![]() , above, we
get
, above, we
get
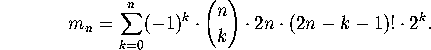
By symmetry, we know that ![]() , must be divisible by
, must be divisible by ![]() .
Pulling
this factor out in front, we can write
.
Pulling
this factor out in front, we can write
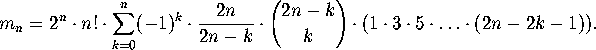
The first few values of ![]() are shown in Table 1.
are shown in Table 1.

Table 1: Relaxed ménage numbers
For the ménage problem, we proceed just as before, only now we
restrict the set S of seatings to those where men and women
alternate. The number of these seatings is ![]() : two ways to
choose which seats are for men and which for women; n! ways to
seat the men in the men's seats; n! ways to seat the women in the
women's seats. Just as before, we have
: two ways to
choose which seats are for men and which for women; n! ways to
seat the men in the men's seats; n! ways to seat the women in the
women's seats. Just as before, we have
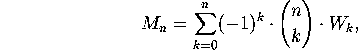
where ![]() denotes the number of alternating seatings under which a
specified set of k couples all end up sitting together. This time we
have
denotes the number of alternating seatings under which a
specified set of k couples all end up sitting together. This time we
have
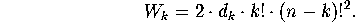
(Decide which are men's seats and which women's, where the k
couples go, which couple goes where, and where the n-k men and n-k
women go.) Plugging in for ![]() yields
yields
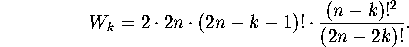
Plugging this expression for ![]() into the formula for
into the formula for ![]() above, we
get
above, we
get
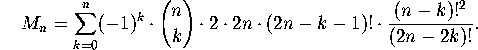
By symmetry, we know that ![]() must be divisible by
must be divisible by ![]() . Pulling
this factor out
in front, we can write
. Pulling
this factor out
in front, we can write
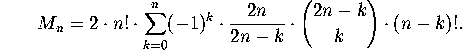
The first few values of ![]() are shown in Table 2.
are shown in Table 2.
The solution that we have just given is completely straight-forward and elementary, yet we have said that the ménage problem is still generally regarded to be tricky. How can this be? The answer can be given in two words: ``Ladies first.'' It apparently never occurred to anyone who looked at the problem not to seat the ladies first (or in a few cases, the gentlemen). Thus Kaplansky and Riordan 16] : ``We may begin by fixing the position of husbands or wives, say wives for courtesy's sake.''
Seating the ladies first ``reduces'' the ménage problem to a problem of permutations with restricted position. Unfortunately, this new problem is more difficult than the problem we began with, as we may judge from the cleverness of Kaplansky's solution [5]:
We now restate the problème des ménages in the usual fashion by observing that the answer is, where
is the number of permutations of
which do not satisfy any of the following 2n conditions: 1 is 1st or 2nd, 2 is 2nd or 3rd,..., n is nth or 1st. Now let us select a subset of k conditions from the above 2n and inquire how many permutations of
there are which satisfy all k; the answer is ( n Ñ k ) ! or 0 according as the k conditions are compatible or not. If we further denote by
the number of ways of selecting k compatible conditions from the 2n, we have, by the familiar argument of inclusion and exclusion,
. It remains to evaluate
, for which purpose we note that the 2n conditions, when arrayed in a circle, have the property that only consecutive ones are not compatible....
Of course ![]() , so we see how, by choosing to view the
constraints as arrayed in a circle, Kaplansky has gotten back on the
track of the straight-forward solution. We can only admire
Kaplansky's cleverness in rediscovering the circle, and regret the
tradition of seating the ladies first that made such cleverness
necessary.
, so we see how, by choosing to view the
constraints as arrayed in a circle, Kaplansky has gotten back on the
track of the straight-forward solution. We can only admire
Kaplansky's cleverness in rediscovering the circle, and regret the
tradition of seating the ladies first that made such cleverness
necessary.
It appears that it was only the tradition of seating the ladies first
that made the ménage problem seem in any way difficult. We may
speculate that, were it not for this tradition, it would not have
taken half a century to discover Touchard's formula for ![]() . Of all the
ways in which sexism has held back the advance of mathematics,
this may well be the most peculiar. (But see Exercise 2.)
. Of all the
ways in which sexism has held back the advance of mathematics,
this may well be the most peculiar. (But see Exercise 2.)
We list here, in the guise of exercises, some questions that you may want to explore with the help of the references listed.