Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

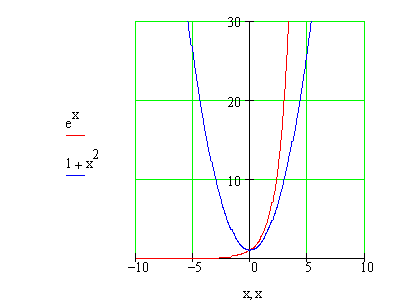
Contents In this lecture we consider an extended application of the ideas of the first four lectures, namely, modeling AIDS data. Quick Question How many solutions does the equation ex − x2 − 1 = 0 have? Answer Outline Outline for Case Study: Modeling with Elementary Functions Textbook Sec. 1.7, Case Study: Modeling with Elementary Functions Today's Homework Log into WebWorK Quiz Case Study: Modeling with Elementary Functions Quiz Examples A succession of forest fires has been decimating the countryside. A table of data is available, giving the days elapsed and acres destroyed. Two functions have been suggested to model the data. Which one is a better fit? After examining the data in the table, it is suggested that since the amount of damage is increasing so quickly, perhaps an exponential function would be a better fit. Is this true? Find the best-fit exponential function and determine if it does in fact model the data more precisely. Use the two polynomials suggested in example 1 to predict the number of acres Use the two polynomials suggested in example 1 to predict the number of acres destroyed after 30, 40, and 50 days. It turns out that after 30 days, the number of acres destroyed was 25100. What was the percentage error in each of your estimates? How does this reflect on your choice of modeling function? Applets Fitting AIDS Data Videos Sum of Squared Errors and Comparing Two Lines

Lecture 4 | Index | Lecture 6