Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

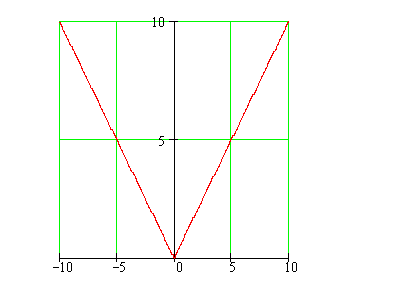
Contents In this lecture we continue the discussion of tangent lines, and define the derivative of a function at a point. (There should be drum rolls and much clapping in the background here. The definition of the derivative has been our goal from the first lecture.) Quick Question Does this function have a unique tangent line at x = 0? Answer Outline Outline for The Derivative Textbook Tangent Lines and their Slopes The Derivative Today's Homework Log into WebWorK Quiz Tangent Lines and their Slopes Quiz The Derivative Quiz Examples Let f(x) = x2 and g(x) = x. Find (f + g)'(4). Does this equal f '(4) + g'(4)? Draw the derivative of a given graph. Let g(x) = 1/x. Find g'(x), g''(x), and g'''(x), and graph them. Can you find a formula for the nth derivative of g(x)? Videos Compute the derivative of f(x) = √(x + 2) using the limit definition of derivative Given the graph of a smooth curve, draw its derivative Given the graph of a curve with corners, draw its derivative

Lecture 8 | Index | Lecture 10