Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

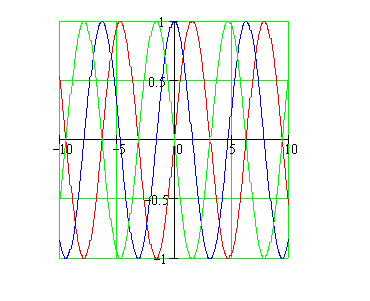
Contents In this lecture we continue our search for differentiation formulas by computing the derivatives of the standard trig functions. Quick Question What are the three functions whose graphs are shown? Answer Outline Outline for Derivatives of Trigonometric Functions Textbook Derivatives of Trigonometric Functions Today's Homework Log into WebWorK Quiz Derivatives of Trigonometric Functions Quiz Examples Consider a circle with a central angle θ, a chord d, arc s, and radius r. Find the limit of s/d as θ approaches 0. A pilot flying at 3 miles above the ground at 600 miles per hour sights the airport with a spotting scope. How fast must she turn the scope when the angle between the path and plane is 40o to keep the scope pointed at the airport? A block at the end of a spring is stretched past its rest position and released. Its position at time t is given by the formula d(t) = 4cos(t). Find the velocity of the spring at time t. When does the block move fastest? Applets Limit of sin(x)/x as x approaches 0 Videos Find derivative of cos(x2) Compute the derivative of x2·sin(√x)

Lecture 10 | Index | Lecture 12