Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

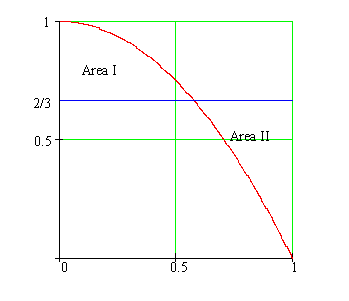
Contents In this lecture we study something called the "Mean Value Theorem." This theorem allows us to take an "at-a-point" concept like the derivative and use it to study the global behavior of a function. We will also learn how to differentiate a function for which we do not have an explicit formula. Quick Question Suppose Area I (above the blue line and below the parabola) equals Area II (above the parabola and below the blue line). What is the total area enclosed by the parabola? Answer Outline Outlines for The Mean Value Theorem Implicit Differentiation Textbook The Mean Value Theorem Implicit Differentiation Today's Homework Log into WebWorK Quiz The Mean Value Theorem Quiz Implicit Differentiation Quiz Examples At 7 p.m., a car is traveling at 50 miles per hour. Ten minutes later, the car has slowed to 30 miles per hour. Show that at some time between 7 and 7:10 the car's acceleration is exactly 120, in units of miles per hours squared. At a particular horse race, two horses start at the same time, and finish in a tie. Show that at some time during the race, the horses were running at the same speed. Suppose f is a differentiable function such that f(1) = 20, f'(x) ≥ 3, 1 ≥ x ≥ 6. What is the smallest possible value for f(6)? Find y' by implicit differentiation, where xy = cot(xy). Find the tangent line to an ellipse at a given point. An interesting curve first studied by Nicomedes around 200 B.C. is the conchoid, which has the equation x2y2 = (x + 1)2 (4 – x2). Use implicit differentiation to find a tangent line to this curve at the point (–1, 0). Applets Mean Value Theorem Videos Tangent is positive where function is increasing, negative where function is decreasing 3x2 + 12x x3 + 17 – 12x The second derivative is the derivative of the derivative sin(x2 + 2) sin(2x)

Lecture 11 | Index | Lecture 13