Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

Contents In this lecture we engage in a case study that involves an extended application of calculus. We study water emptying from a cylindrical tank through an outlet hole in the bottom, and develop formulas to answer questions such as, "How long will it take the tank to empty?" This investigation is meant to be an example of the kind of modeling possible with differential calculus, and is the capstone to lectures 6-16. 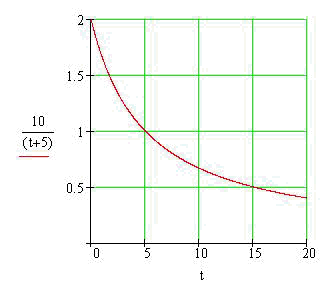Quick Question When is the tank empty if this graph shows the number of gallons of water remaining in the tank after t seconds? Answer Outline Outline for Case Study: Torricelli's Law Textbook Case Study: Torricelli's Law Today's Homework Log into WebWorK Quiz Case Study: Torricelli's Law Quiz Examples For a given quantity of gas, Boyle's Law states that the pressure exerted by the gas and the volume it takes up are inversely proportional to each other; that is, P = C/V or equivalently PV = C. Assume that the volume changes over time, so V is a function of t. Find the rate of change of the pressure with respect to time in two different ways: in terms of V, dV/dt only, and in terms of P, dV/dt only. Assume that the pressure exerted by the gas is modeled by the equation √(1 + t). Determine the rates at which the pressure and the volume are changing, with respect to time. A gas occupies 6.52 liters at a pressure of 0.92 atmospheres. Determine the volume if the pressure is increased to 1.44 atmospheres. If the pressure change is linear and occurs over a period of 5 seconds, what is the instantaneous rate of change of the volume with respect to time at 2 seconds? Applets Function Grapher Videos Boyle's Law PV = kT Relate dP/dt to dV/dt in Boyle's Law

Lecture 15 | Index | Lecture 17