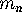of ways of seating 
couples around a circular table, so that no one sits next to his or her
partner. This is nearly the same as the ménage problem, only now we
have relaxed the requirement that men and women alternate.
We begin with an apparently simpler problem, called the relaxed
ménage problem, which asks for the number 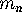of ways of seating
couples around a circular table, so that no one sits next to his or her
partner. This is nearly the same as the ménage problem, only now we
have relaxed the requirement that men and women alternate.
To determine 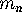, we begin with the set 
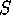of all 
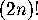ways of
seating the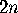 
individuals around the table, and use inclusion-exclusion
on the set of couples who end up sitting together. Let us
call the elements of 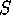seatings, and let us denote by 
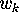the number
of seatings under which some specified set of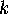 
couples (and
possibly some other couples) end up sitting together. Clearly,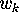
does not depend on the particular set of 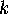couples we choose, and so,
by the principle of inclusion and exclusion, we have
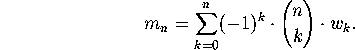
To finish the enumeration, we must compute 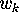. Assume 
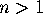. Let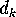 
denote the number of ways of placing 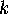non-overlapping unlabeled
dominos on 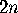vertices arranged in a circle.
(See Figure 1.)
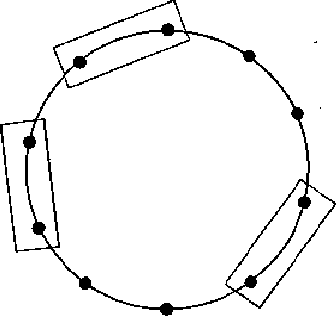
Figure 1: Non-overlapping dominos
Then
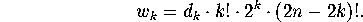
(Decide where th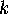e couples go, and which couple goes where, and
which partner
takes which seat, and where the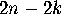 
individuals go.) So now we
have only to
compute the 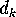's. This is a routine combinatorial problem. The
answer is
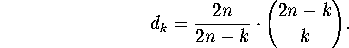
(See Ryser [11], pp. 33-34, or Exercise 1 below). This yields
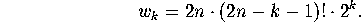
Plugging this expression for 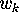into the formula for 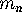, above, we
get
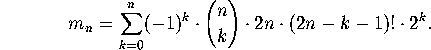
By symmetry, we know that 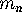, must be divisible by 
.
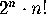Pulling
this factor out in front, we can write
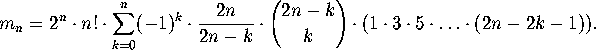
The first few values of 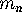are shown in Table 1.
